Hyperbolisk geometri - Hyperbolic geometry

Linjer genom en given punkt P och asymptotisk till linje R

En triangel nedsänkt i ett sadelformat plan (en hyperbolisk paraboloid ), tillsammans med två divergerande ultra-parallella linjer

I matematik , hyperbolisk geometri (även kallad Lobachevskian geometri eller Bolyai - Lobachevskian geometri ) är en icke-Euklidisk geometri . Det parallella postulatet för den euklidiska geometrin ersätts med:

För varje given linje R och punkten P inte på R , i det plan som innehåller både linjen R och punkten P det finns åtminstone två distinkta linjer genom P som inte korsar R .

(Jämför den ovan med Playfair s axiom , den moderna versionen av Euklides 's parallellaxiomet .)

Hyperbolisk plangeometri är också geometrin för sadelytor och pseudosfäriska ytor , ytor med en konstant negativ Gaussisk krökning .

En modern användning av hyperbolisk geometri finns i teorin om speciell relativitetsteori , särskilt Minkowski -modellen .

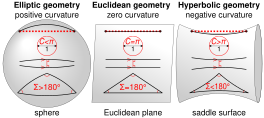
När geometrar först insåg att de arbetade med något annat än den vanliga euklidiska geometrin, beskrev de deras geometri under många olika namn; Felix Klein gav äntligen ämnet namnet hyperbolisk geometri för att inkludera den i den nu sällan använda sekvensen elliptisk geometri ( sfärisk geometri ), parabolisk geometri ( euklidisk geometri ) och hyperbolisk geometri. I det forna Sovjetunionen kallas det vanligtvis Lobachevskian geometri, uppkallad efter en av dess upptäckare, den ryska geometern Nikolai Lobachevsky .

Den här sidan handlar främst om den 2-dimensionella (plana) hyperboliska geometrin och skillnaderna och likheterna mellan euklidisk och hyperbolisk geometri. Se hyperboliskt utrymme för mer information om hyperbolisk geometri utvidgad till tre och fler dimensioner.

Egenskaper

Förhållande till euklidisk geometri

Jämförelse av elliptiska, euklidiska och hyperboliska geometrier i två dimensioner

Hyperbolisk geometri är närmare besläktad med euklidisk geometri än den verkar: den enda axiomatiska skillnaden är parallellpostulatet . När det parallella postulatet tas bort från den euklidiska geometrin är den resulterande geometrin absolut geometri . Det finns två sorters absolut geometri, euklidisk och hyperbolisk. Alla satser om absolut geometri, inklusive de första 28 förslagen i bok ett av Euklides element , är giltiga i euklidisk och hyperbolisk geometri. Förslag 27 och 28 i bok ett av Euklids element bevisar förekomsten av parallella/icke-skärande linjer.

Denna skillnad har också många konsekvenser: begrepp som är ekvivalenta i euklidisk geometri är inte ekvivalenta i hyperbolisk geometri; nya begrepp måste introduceras. På grund av parallellismens vinkel har hyperbolisk geometri vidare en absolut skala , ett förhållande mellan avstånds- och vinkelmätningar.

Rader

Enstaka linjer i hyperbolisk geometri har exakt samma egenskaper som enkla raka linjer i euklidisk geometri. Till exempel definierar två punkter unikt en linje och radsegment kan förlängas oändligt.

Två skärande linjer har samma egenskaper som två skärande linjer i euklidisk geometri. Till exempel kan två distinkta linjer skär varandra i inte mer än en punkt, skärande linjer bildar lika motsatta vinklar och angränsande vinklar för skärande linjer är kompletterande .

När en tredje linje introduceras kan det finnas egenskaper hos korsande linjer som skiljer sig från korsande linjer i euklidisk geometri. Till exempel, med tanke på två skärande linjer finns det oändligt många linjer som inte skär någon av de givna linjerna.

Dessa egenskaper är alla oberoende av modellen som används, även om linjerna kan se radikalt annorlunda ut.

Icke-skärande / parallella linjer

Linjer genom en given punkt P och asymptotisk till linje R .

Icke-skärande linjer i hyperbolisk geometri har också egenskaper som skiljer sig från icke-skärande linjer i euklidisk geometri :

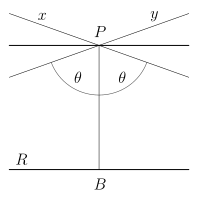
För varje linje R och någon punkt P , som inte ligger på R , i det plan som innehåller linjen R och punkten P det finns åtminstone två distinkta linjer genom P som inte korsar R .

Detta innebär att det finns genom P ett oändligt antal i samma plan liggande linjer som inte korsar R .

Dessa icke-skärande linjer är indelade i två klasser:

Två av raderna ( x och y i diagrammet) är begränsande paralleller (kallas ibland kritiskt parallell, horoparallell eller bara parallell): det finns en i riktningen för var och en av de ideala punkterna vid "ändarna" av R , som asymptotiskt närmar sig R , kommer alltid närmare R , men möter det aldrig.
Alla andra icke-skärande linjer har en punkt med minimiavstånd och avviker från båda sidorna av den punkten, och kallas ultraparallell , divergerande parallella eller ibland icke-skärande.

Vissa geometrar använder helt enkelt uttrycket " parallella linjer" för att betyda " begränsande parallella linjer", med ultraparallella linjer som betyder bara icke-skärande .

Dessa begränsande paralleller gör en vinkel θ med PB ; denna vinkel beror endast på planetens Gaussiska krökning och avståndet PB och kallas parallellismens vinkel .

För ultraparallelllinjer säger ultraparallelsatsen att det finns en unik linje i det hyperboliska planet som är vinkelrätt mot varje par av ultraparallelllinjer.

Cirklar och skivor

I hyperbolisk geometri är omkretsen av en cirkel med radie r större än . ${\ displaystyle 2 \ pi r}$

Låt , var är planetens Gauss -krökning . I hyperbolisk geometri, är negativ, så kvadratroten har ett positivt tal. ${\ displaystyle R = {\ frac {1} {\ sqrt {-K}}}}$ ${\ displaystyle K}$ ${\ displaystyle K}$

Då är omkretsen för en cirkel med radie r lika med:

{\ displaystyle 2 \ pi R \ sinh {\ frac {r} {R}} \ ,.}

Och området på den medföljande skivan är:

{\ displaystyle 4 \ pi R^{2} \ sinh^{2} {\ frac {r} {2R}} = 2 \ pi R^{2} \ left (\ cosh {\ frac {r} {R} } -1 \ höger) \ ,.}

Därför är förhållandet mellan en cirkels omkrets och dess radie i hyperbolisk geometri alltid strikt större än , även om den kan göras godtyckligt nära genom att välja en tillräckligt liten cirkel. ${\ displaystyle 2 \ pi}$

Om planetens Gauss -krökning är -1 är den geodesiska krökningen för en cirkel med radie r : ${\ displaystyle {\ frac {1} {\ tanh (r)}}}$

Hypercyklar och horocykler

Hypercykel och pseudogon i Poincare -diskmodellen

I hyperbolisk geometri finns det ingen linje som alla punkter är lika långt från en annan linje. Istället ligger de punkter som alla har samma ortogonala avstånd från en given linje på en kurva som kallas en hypercykel .

Annan särskild kurva är horocycle , en kurva vars normal radier ( vinkelräta linjer) är alla begränsande parallella med varandra (alla konvergera asymptotiskt i en riktning till samma idealiskt , i mitten av horocycle).

Genom varje par punkter finns det två horocykler. Horocyklernas centrum är de ideala punkterna för den vinkelräta halvan av linjesegmentet mellan dem.

Med tanke på tre olika punkter ligger de alla antingen på en linje, hypercykel , horocykel eller cirkel.

Linjesegmentets längd är den kortaste längden mellan två punkter. Båglängden för en hypercykel som förbinder två punkter är längre än linjesegmentets och kortare än en horocykel och förbinder samma två punkter. Arlängden för båda horocyklerna som förbinder två punkter är lika. Båglängden på en cirkel mellan två punkter är större än båglängden på en horocykel som förbinder två punkter.

Om planetens Gauss -krökning är -1 är den geodesiska krökningen för en horocykel 1 och för en hypercykel mellan 0 och 1.

Trianglar

Till skillnad från euklidiska trianglar, där vinklarna alltid lägger till π -radianer (180 °, en rak vinkel ), är hyperbolisk geometri summan av vinklarna i en hyperbolisk triangel alltid strikt mindre än π -radianer (180 °, en rak vinkel ). Skillnaden kallas defekten .

Arean av en hyperbolisk triangel ges av sin defekt i radianer multiplicerad med R ² . Som en konsekvens har alla hyperboliska trianglar ett område som är mindre än eller lika med R ² π. Området för en hyperbolisk ideal triangel där alla tre vinklarna är 0 ° är lika med detta maximum.

Precis som i euklidisk geometri har varje hyperbolisk triangel en cirkel . I hyperbolisk geometri, om alla tre av dess hörn ligger på en horocykel eller hypercykel , så har triangeln ingen avgränsad cirkel .

Som i sfärisk och elliptisk geometri , i hyperbolisk geometri om två trianglar är lika måste de vara kongruenta.

Vanlig apeirogon

en apeirogon och begränsad horocykel i Poincare -skivmodellen

En speciell polygon i hyperbolisk geometri är den vanliga apeirogon , en enhetlig polygon med ett oändligt antal sidor.

I euklidisk geometri är det enda sättet att konstruera en sådan polygon att få sidlängderna att nollas och apeirogon går inte att skilja från en cirkel, eller få de inre vinklarna att tendera till 180 grader och apeirogon närmar sig en rak linje.

I hyperbolisk geometri har emellertid en vanlig apeirogon sidor av vilken längd som helst (dvs den förblir en polygon).

Sid- och vinkelhärdarna kommer, beroende på sidlängden och vinkeln mellan sidorna, att vara begränsande eller avvikande parallella (se rader ovan ). Om bisektorerna är begränsande parallella kan apeirogon skrivas in och begränsas av koncentriska horocykler .

Om bisektorerna divergerar parallellt kan en pseudogon (klart annorlunda än en apeirogon) skrivas in i hypercyklar (alla hörn är samma avstånd för en linje, axeln, även mittpunkten för sidosegmenten är alla lika långt från samma axel. )

Tessellationer

Rhombitriheptagonal kakling av det hyperboliska planet, sett i Poincaré -skivmodellen

Liksom det euklidiska planet är det också möjligt att tessellera det hyperboliska planet med regelbundna polygoner som ansikten .

Det finns ett oändligt antal enhetliga plattor baserade på Schwarz -trianglarna ( p q r ) där 1/ p + 1/ q + 1/ r <1, där p , q , r är varje ordning av reflektionssymmetri vid tre punkter i grundläggande domän triangel , symmetri gruppen är en hyperbolisk triangel grupp . Det finns också oändligt många enhetliga plattor som inte kan genereras från Schwarz -trianglar, vissa kräver till exempel fyrhörningar som grundläggande domäner.

Standardiserad gaussisk krökning

Även om hyperbolisk geometri gäller för alla ytor med en konstant negativ Gaussisk krökning , är det vanligt att man antar en skala där krökningen K är -1.

Detta resulterar i att vissa formler blir enklare. Några exempel är:

Arean av en triangel är lika med dess vinkeldefekt i radianer .
Arean på en horocyklisk sektor är lika med längden på dess horocykliska båge.
En båge i en horocykel så att en linje som är tangent vid ena ändpunkten begränsar parallellt med radien genom den andra slutpunkten har en längd av 1.
Förhållandet mellan ljusbågslängderna mellan två radier av två koncentriska horocykler där horocyklerna är ett avstånd 1 från varandra är e : 1.

Kartesianska koordinatsystem

I hyperbolisk geometri är summan av vinklarna i en fyrkant alltid mindre än 360 grader, och hyperboliska rektanglar skiljer sig mycket från euklidiska rektanglar eftersom det inte finns några lika långa linjer, så en riktig euklidisk rektangel skulle behöva omges av två linjer och två hypercykler . Dessa komplicerar alla koordinatsystem.

Det finns dock olika koordinatsystem för hyperbolisk plangeometri. Alla är baserade på att välja en punkt (ursprunget) på en vald riktad linje ( x -axeln) och efter det finns många val.

Lobachevski -koordinaterna x och y hittas genom att släppa en vinkelrätt på x -axeln. x kommer att vara etiketten på foten av den vinkelräta. y kommer att vara avståndet längs vinkelrätt på den givna punkten från dess fot (positivt på ena sidan och negativt på den andra).

Ett annat koordinatsystem mäter avståndet från punkten till horocykeln genom ursprunget centrerat runt och längden längs denna horocykel. ${\ displaystyle (0,+\ infty)}$

Andra koordinatsystem använder Klein -modellen eller Poincare -diskmodellen som beskrivs nedan och tar de euklidiska koordinaterna som hyperboliska.

Distans

Konstruera ett kartesianskt koordinatsystem enligt följande. Välj en linje ( x -axeln) i det hyperboliska planet (med en standardiserad krökning av -1) och märk punkterna på den med avståndet från en ursprungspunkt ( x = 0) på x -axeln (positiv på ena sidan och negativt på den andra). För vilken punkt som helst i planet kan man definiera koordinaterna x och y genom att släppa en vinkelrätt på x -axeln. x kommer att vara etiketten på foten av den vinkelräta. y kommer att vara avståndet längs vinkelrätt på den givna punkten från dess fot (positivt på ena sidan och negativt på den andra). Då blir avståndet mellan två sådana punkter

{\ displaystyle \ operatorname {dist} (\ langle x_ {1}, y_ {1} \ rangle, \ langle x_ {2}, y_ {2} \ rangle) = \ operatorname {arcosh} \ left (\ cosh y_ { 1} \ cosh (x_ {2} -x_ {1}) \ cosh y_ {2}-\ sinh y_ {1} \ sinh y_ {2} \ right) \ ,.}

Denna formel kan härledas från formlerna om hyperboliska trianglar .

Den motsvarande metrisk tensor är: . ${\ displaystyle (\ mathrm {d} s)^{2} = \ cosh^{2} y \, (\ mathrm {d} x)^{2}+(\ mathrm {d} y)^{2} }$

I detta koordinatsystem är raka linjer antingen vinkelräta mot x -axeln (med ekvation x = en konstant) eller beskrivs med ekvationer i formen

{\ displaystyle \ tanh y = A \ cosh x+B \ sinh x \ quad {\ text {when}} \ quad A^{2} <1+B^{2}}

där A och B är riktiga parametrar som kännetecknar den raka linjen.

Historia

Sedan publiceringen av Euclids element omkring 300 fvt gjorde många geometrar försök att bevisa parallellpostulatet . Vissa försökte bevisa det genom att anta dess negation och försöka härleda en motsägelse . Främst bland dessa var Proclus , Ibn al-Haytham (Alhacen), Omar Khayyám , Nasīr al-Din al-Tūsī , Witelo , Gersonides , Alfonso och senare Giovanni Gerolamo Saccheri , John Wallis , Johann Heinrich Lambert och Legendre . Deras försök var dömda att misslyckas (som vi nu vet är parallellpostulatet inte bevisbart från de andra postulaten), men deras ansträngningar ledde till upptäckten av hyperbolisk geometri.

Satserna Alhacen, Khayyam och al-Tūsī om fyrsidiga , inklusive Ibn al-Haytham – Lambert fyrkant och Khayyam – Saccheri fyrkant , var de första satserna om hyperbolisk geometri. Deras verk om hyperbolisk geometri hade ett stort inflytande på dess utveckling bland senare europeiska geometrar, inklusive Witelo, Gersonides, Alfonso, John Wallis och Saccheri.

På 1700 -talet introducerade Johann Heinrich Lambert de hyperboliska funktionerna och beräknade området för en hyperbolisk triangel .

1800-talets utveckling

På 1800 -talet utforskades hyperbolisk geometri i stor utsträckning av Nikolai Ivanovich Lobachevsky , János Bolyai , Carl Friedrich Gauss och Franz Taurinus . Till skillnad från sina föregångare, som bara ville eliminera det parallella postulatet från axiomen för den euklidiska geometrin, insåg dessa författare att de hade upptäckt en ny geometri. Gauss skrev i ett brev från 1824 till Franz Taurinus att han hade konstruerat det, men Gauss publicerade inte hans verk. Gauss kallade det " icke-euklidisk geometri " vilket fick flera moderna författare att fortsätta betrakta "icke-euklidisk geometri" och "hyperbolisk geometri" som synonymer. Taurinus publicerade resultat om hyperbolisk trigonometri 1826, hävdade att hyperbolisk geometri är självkonsistent, men trodde fortfarande på den speciella rollen som den euklidiska geometrin. Det fullständiga systemet för hyperbolisk geometri publicerades av Lobachevsky 1829/1830, medan Bolyai upptäckte det oberoende och publicerades 1832.

År 1868 tillhandahöll Eugenio Beltrami modeller (se nedan) av hyperbolisk geometri och använde detta för att bevisa att hyperbolisk geometri var konsekvent om och bara om euklidisk geometri var det.

Termen "hyperbolisk geometri" introducerades av Felix Klein 1871. Klein följde ett initiativ av Arthur Cayley för att använda transformationerna av projektiv geometri för att producera isometrier . Idén använde en konisk sektion eller kvadrisk för att definiera en region, och använde korsförhållande för att definiera ett mått . De projektiva transformationerna som lämnar den koniska sektionen eller kvadralt stabila är isometrier. "Klein visade att om Cayley -absoluten är en verklig kurva så är delen av det projektiva planet i dess inre isometrisk mot det hyperboliska planet ..."

För mer historia, se artikel om icke-euklidisk geometri och referenserna Coxeter och Milnor .

Filosofiska konsekvenser

Upptäckten av hyperbolisk geometri fick viktiga filosofiska konsekvenser. Före upptäckten såg många filosofer (till exempel Hobbes och Spinoza ) på filosofisk noggrannhet när det gäller den "geometriska metoden", med hänvisning till resonemangsmetoden som används i Euclids element .

Kant i Critique of Pure Reason kom till slutsatsen att rymden (i euklidisk geometri ) och tid inte upptäcks av människor som objektiva drag i världen, utan är en del av en oundviklig systematisk ram för att organisera våra erfarenheter.

Det sägs att Gauss inte publicerade något om hyperbolisk geometri av rädsla för " Boeotians uppståndelse ", vilket skulle förstöra hans status som princeps mathemataticorum (latin, "matematikerfyrsten"). "Boeotians uppståndelse" kom och gick, och gav upphov till stora förbättringar i matematisk noggrannhet , analytisk filosofi och logik . Hyperbolisk geometri visade sig slutligen vara konsekvent och är därför en annan giltig geometri.

Universums geometri (endast rumsliga dimensioner)

Eftersom euklidisk, hyperbolisk och elliptisk geometri alla är konsekvent, uppstår frågan: vilken är rymdens verkliga geometri, och om den är hyperbolisk eller elliptisk, vad är dess krökning?

Lobachevsky hade redan försökt mäta universums krökning genom att mäta parallaxen till Sirius och behandla Sirius som den idealiska punkten för en parallellismvinkel . Han insåg att hans mätningar inte var tillräckligt exakta för att ge ett definitivt svar, men han kom fram till att om universums geometri är hyperbolisk, så är den absoluta längden minst en miljon gånger diametern på jordens bana (2 000 000 AU , 10 parsek ). Vissa hävdar att hans mätningar var metodiskt bristfälliga.

Henri Poincaré , med sin sfär-world tankeexperiment , kom till slutsatsen att vardagen inte nödvändigtvis utesluta andra geometrier.

Den geometriseringsförmodan ger en fullständig lista över åtta möjligheter för grundläggande geometri vårt utrymme. Problemet med att bestämma vilken som gäller är att för att nå ett definitivt svar måste vi kunna titta på extremt stora former - mycket större än någonting på jorden eller kanske till och med i vår galax.

Universums geometri (särskild relativitet)

Särskild relativitet placerar rum och tid på lika villkor, så att man betraktar geometrin för en enhetlig rymdtid istället för att betrakta rum och tid separat. Minkowski-geometri ersätter galileisk geometri (som är det tredimensionella euklidiska utrymmet med den galileiska relativitetens tid ).

I relativitetsteori, i stället för att överväga euklidiska, elliptiska och hyperboliska geometrier, är lämpliga geometrier att överväga Minkowski-utrymme , de Sitter-utrymme och anti-de Sitter-utrymme , motsvarande noll, positiv respektive negativ krökning.

Hyperbolisk geometri går in i särskild relativitet genom snabbhet , som står för hastighet och uttrycks av en hyperbolisk vinkel . Studiet av denna hastighetsgeometri har kallats kinematisk geometri . Utrymmet för relativistiska hastigheter har en tredimensionell hyperbolisk geometri, där avståndsfunktionen bestäms från de relativa hastigheterna för "närliggande" punkter (hastigheter).

Fysiska förverkliganden av det hyperboliska planet

Det hyperboliska planet är ett plan där varje punkt är en sadelpunkt . Det finns olika pseudosfärer i det euklidiska utrymmet som har ett ändligt område med konstant negativ Gauss -krökning.

Enligt Hilberts sats är det inte möjligt att isometriskt fördjupa ett komplett hyperboliskt plan (en fullständig regelbunden yta med konstant negativ Gaussisk krökning ) i ett tredimensionellt euklidiskt utrymme.

Andra användbara modeller för hyperbolisk geometri finns i det euklidiska utrymmet, där metriken inte bevaras. En särskilt välkänd pappersmodell baserad på pseudosfären beror på William Thurston .

En samling virkade hyperboliska plan, i imitation av ett korallrev, av Institute For Figuring

En korall med liknande geometri på Great Barrier Reef

Konsten att virka har använts (se Matematik och fiberkonst § Stickning och virkning ) för att demonstrera hyperboliska plan, den första demonstrationen har gjorts av Daina Taimiņa .

År 2000 demonstrerade Keith Henderson en pappersmodell som var snabb att göra, kallad " hyperbolisk fotboll " (närmare bestämt en avkortad triangelformad kakelplatta ).

Instruktioner om hur man gör ett hyperboliskt täcke, designat av Helaman Ferguson , har gjorts tillgängliga av Jeff Weeks .

Modeller av det hyperboliska planet

Det finns olika pseudosfäriska ytor som för ett stort område har en konstant negativ Gaussisk krökning, varvid pseudosfären är den mest välkända av dem.

Men det är lättare att göra hyperbolisk geometri på andra modeller.

Poincaré -skivmodell med stympad triheptagonal kakel

Linjer genom en given punkt och parallell med en given linje, illustrerad i Poincaré -diskmodellen

Det finns fyra modeller som vanligtvis används för hyperbolisk geometri: Klein-modellen , Poincaré-diskmodellen , Poincaré-halvplansmodellen och Lorentz- eller hyperboloidmodellen . Dessa modeller definierar ett hyperboliskt plan som uppfyller axiomen för en hyperbolisk geometri. Trots deras namn introducerades de tre första nämnda ovan som modeller av hyperboliskt utrymme av Beltrami , inte av Poincaré eller Klein . Alla dessa modeller kan förlängas till fler dimensioner.

Beltrami – Klein -modellen

Den Beltrami-Klein-modellen , även känd som projektiva disk modell, Klein disk modell och Klein-modellen , är uppkallad efter Eugenio Beltrami och Felix Klein .

För de två dimensionerna använder denna modell interiören i enhetscirkeln för det fullständiga hyperboliska planet , och ackorden i denna cirkel är de hyperboliska linjerna.

För högre dimensioner använder denna modell interiören i enhetsbollen , och ackorden i denna n -boll är de hyperboliska linjerna.

Denna modell har fördelen att linjer är raka, men nackdelen att vinklar är snedvridna (kartläggningen är inte överensstämmande ), och att cirklar inte representeras som cirklar.
Avståndet i denna modell är halva logaritmen för korsförhållandet , som introducerades av Arthur Cayley i projektiv geometri .

Poincaré -diskmodellen

Den Poincaré disk modell , även känd som det konforma disk modell, utnyttjar också det inre av enhetscirkeln , men linjer representeras av cirkelbågar som är ortogonala till gränscirkeln, plus diametrar på gränscirkeln.

Denna modell bevarar vinklar och är därmed konform . Alla isometrier inom denna modell är därför Möbius -transformationer .
Cirklar helt inuti skivan förblir cirklar även om den euklidiska mitten av cirkeln är närmare mitten av skivan än den hyperboliska mitten av cirkeln.
Horocykler är cirklar inom skivan som tangerar gränscirkeln, minus kontaktpunkten.
Hypercyklar är öppna ackord och cirkelbågar inom skivan som slutar på gränscirkeln vid icke-ortogonala vinklar.

Halvplansmodellen Poincaré

Den Poincaré halv-planmodellen tar en halva av det euklidiska planet, som avgränsas av en linje B av planet, för att vara en modell av den hyperboliska planet. Linje B ingår inte i modellen.

Det euklidiska planet kan ses som ett plan med det kartesiska koordinatsystemet och x-axeln tas som linje B och halvplanet är den övre halvan ( y > 0) av detta plan.

Hyperboliska linjer är sedan antingen halv-cirklar ortogonala till B eller strålar vinkelrät mot B .
Längden på ett intervall på en stråle ges med logaritmiskt mått så att det är invariant under en homotisk transformation ${\ displaystyle (x, y) \ mapsto (x, \ lambda y), \ quad \ lambda> 0.}$
Precis som Poincaré -diskmodellen bevarar denna modell vinklar och är därmed konform . Alla isometrier inom denna modell är därför Möbius -transformationer av planet.
Halvplansmodellen är gränsen för Poincaré-skivmodellen vars gräns tangerar B vid samma punkt medan skivmodellens radie går till oändlighet.

Hyperboloidmodellen

Den hyperboloid modell eller Lorentz modell utnyttjar en två-dimensionell hyperboloid rotationsyta (av två ark, men med användning av en) inbäddad i 3-dimensionell Minkowski utrymme . Denna modell krediteras generellt Poincaré, men Reynolds säger att Wilhelm Killing använde denna modell 1885

Denna modell har direkt tillämpning på särskild relativitet , eftersom Minkowski 3-space är en modell för rymdtid , som undertrycker en rumslig dimension. Man kan ta hyperboloiden för att representera de händelser som olika rörliga observatörer, som strålar utåt i ett rymdplan från en enda punkt, kommer att nå på en bestämd riktig tid .
Det hyperboliska avståndet mellan två punkter på hyperboloiden kan sedan identifieras med den relativa hastigheten mellan de två motsvarande observatörerna.
Modellen generaliserar direkt till en ytterligare dimension, där tredimensionell hyperbolisk geometri relaterar till Minkowski 4-rymd.

Halvklotsmodellen

Den halvklotet modellen inte ofta som modell av sig själv, men den fungerar som ett användbart verktyg för att visualisera transformationer mellan de andra modellerna.

Halvklotsmodellen använder den övre halvan av enhetens sfär : ${\ displaystyle x^{2}+y^{2}+z^{2} = 1, z> 0.}$

De hyperboliska linjerna är halvcirklar ortogonala till gränsen för halvklotet.

Halvklotsmodellen är en del av en Riemann -sfär , och olika projektioner ger olika modeller av det hyperboliska planet:

Stereografisk projektion från på planet projicerar motsvarande punkter på Poincaré -diskmodellen ${\ displaystyle (0,0, -1)}$ ${\ displaystyle z = 0}$
Stereografisk projektion från på ytan projicerar motsvarande punkter på hyperboloidmodellen ${\ displaystyle (0,0, -1)}$ ${\ displaystyle x^{2}+y^{2} -z^{2} =-1, z> 0}$
Stereografisk projektion från på planet projicerar motsvarande punkter på Poincaré halvplansmodell ${\ displaystyle (-1,0,0)}$ ${\ displaystyle x = 1}$
Ortografisk projektion på ett plan projicerar motsvarande punkter på Beltrami – Klein -modellen . ${\ displaystyle z = C}$
Central projektion från mitten av sfären på planet projicerar motsvarande punkter på Gans -modellen ${\ displaystyle z = 1}$

Se vidare: Anslutning mellan modellerna (nedan)

Gans -modellen

1966 föreslog David Gans en plattad hyperboloidmodell i tidskriften American Mathematical Monthly . Det är en ortografisk projektion av hyperboloidmodellen på xy-planet. Denna modell används inte lika mycket som andra modeller men är ändå ganska användbar för att förstå hyperbolisk geometri.

Till skillnad från Klein- eller Poincaré -modellerna använder denna modell hela det euklidiska planet .
Linjerna i denna modell representeras som grenar av en hyperbol .

Bandmodellen

Bandmodellen använder en del av det euklidiska planet mellan två parallella linjer. Avståndet bevaras längs en linje genom mitten av bandet. Om man antar att bandet ges av , ges metriska av . ${\ displaystyle \ {z \ in \ mathbb {C}: | \ operatorname {Im} z | <\ pi /2 \}}$ ${\ displaystyle | dz | \ sec (\ operatorname {Im} z)}$

Anslutning mellan modellerna

Poincaré -skiva, hemisfäriska och hyperboloidmodeller är relaterade genom stereografisk projektion från −1. Beltrami – Klein -modellen är ortografisk projektion från halvklotformad modell. Poincaré halvplansmodell här projicerad från den halvklotformade modellen med strålar från vänster ände av Poincaré-diskmodell.

Alla modeller beskriver i huvudsak samma struktur. Skillnaden mellan dem är att de representerar olika koordinatdiagram som ligger på samma metriska utrymme , nämligen det hyperboliska planet. Det karakteristiska kännetecknet för det hyperboliska planet i sig är att det har en konstant negativ Gaussisk krökning , som är likgiltig mot det koordinatdiagram som används. De geodesics är lika invariant: det vill säga geodesics karta till geodesics enligt koordinattransformation. Hyperbolisk geometri introduceras generellt när det gäller geodesiken och deras korsningar på det hyperboliska planet.

När vi väl valt ett koordinatdiagram (en av "modellerna") kan vi alltid bädda in det i ett euklidiskt utrymme med samma dimension, men inbäddningen är uppenbarligen inte isometrisk (eftersom det euklidiska rymdets krökning är 0). Det hyperboliska utrymmet kan representeras av oändligt många olika diagram; men inbäddningarna i det euklidiska rummet på grund av dessa fyra specifika diagram visar några intressanta egenskaper.

Eftersom de fyra modellerna beskriver samma metriska utrymme kan var och en förvandlas till den andra.

Se till exempel:

Isometrier av det hyperboliska planet

Varje isometri ( transformation eller rörelse ) av det hyperboliska planet till sig själv kan realiseras som sammansättningen av högst tre reflektioner . I n -dimensionellt hyperboliskt utrymme kan upp till n +1 reflektioner behövas. (Dessa gäller också för euklidiska och sfäriska geometrier, men klassificeringen nedan är annorlunda.)

Alla isometrier i det hyperboliska planet kan klassificeras i dessa klasser:

Orientering bevarar
- den identitet isometry - ingenting rör sig; noll reflektioner; noll grader av frihet .
- inversion genom en punkt (halv varv) - två reflektioner genom ömsesidigt vinkelräta linjer som passerar genom den givna punkten, dvs en rotation på 180 grader runt punkten; två frihetsgrader .
- rotation runt en normal punkt - två reflektioner genom linjer som passerar genom den givna punkten (inkluderar inversion som ett specialfall); punkter rör sig på cirklar runt mitten; tre grader av frihet.
- "rotation" runt ett idealiskt (horolation) - två reflektioner genom ledningarna som leder till idealiskt; punkter rör sig längs horocykler centrerade på den ideala punkten; två frihetsgrader.
- translation längs en rak linje - två reflektioner genom linjer vinkelrätt mot den givna linjen; pekar från den givna linjen rör sig längs hypercyklar; tre grader av frihet.
Orientering bakåt
- reflektion genom en linje - en reflektion; två frihetsgrader.
- kombinerad reflektion genom en linje och översättning längs samma linje - reflektionen och översättningen pendlar; tre reflektioner krävs; tre grader av frihet.

Hyperbolisk geometri i konst

MC Eschers berömda tryck Circle Limit III och Circle Limit IV illustrerar den korrekta skivmodellen ( Poincaré -diskmodell ) ganska bra. De vita linjerna i III är inte riktigt geodesiska (de är hypercyklar ), men ligger nära dem. Det är också möjligt att helt tydligt se det negativa krökandet hos det hyperboliska planet genom dess effekt på summan av vinklar i trianglar och rutor.

Till exempel i Circle Limit III tillhör varje hörn tre trianglar och tre rutor. I det euklidiska planet skulle deras vinklar summera till 450 °; dvs en cirkel och en fjärdedel. Av detta ser vi att summan av vinklarna för en triangel i det hyperboliska planet måste vara mindre än 180 °. En annan synlig egenskap är exponentiell tillväxt . I cirkelgräns III , till exempel, kan man se att antalet fiskar inom ett avstånd av n från mitten stiger exponentiellt. Fiskarna har ett lika hyperboliskt område, så området för en boll med radie n måste stiga exponentiellt i n .

Konsten att virka har använts för att demonstrera hyperboliska plan (bilden ovan) med den första gjord av Daina Taimiņa , vars bok Crocheting Adventures with Hyperbolic Planes vann 2009 års bokhandlare/diagrampris för årets udda titel .

HyperRogue är ett roguelike -spel på olika kakel i det hyperboliska planet .

Högre dimensioner

Hyperbolisk geometri är inte begränsad till två dimensioner; en hyperbolisk geometri finns för varje högre antal dimensioner.

Homogen struktur

Hyperboliskt utrymme med dimension n är ett specialfall av ett Riemannian symmetriskt utrymme av icke -kompakt typ, eftersom det är isomorft för kvoten

{\ displaystyle \ mathrm {O} (1, n)/(\ mathrm {O} (1) \ times \ mathrm {O} (n)).}

Den ortogonala gruppen O (1, n ) verkar genom normbevarande transformationer på Minkowski-utrymmet R ^{, n} , och den verkar transitivt på två-arks hyperboloid av norm 1-vektorer. Tidliknande linjer (dvs. de med positiva normtangenter) genom ursprunget passerar genom antipodala punkter i hyperboloiden, så utrymmet för sådana linjer ger en modell för hyperboliskt n -rymd. Den stabilisator av någon särskild linje är isomorf med den produkt av den ortogonala grupper O ( n ) och O (1), där O ( n verkar) på tangentutrymmet av en punkt i hyperboloid, och O (1) återspeglar linjen genom ursprunget. Många av de elementära begreppen i hyperbolisk geometri kan beskrivas i linjära algebraiska termer: geodesiska vägar beskrivs genom korsningar med plan genom ursprunget, dihedrala vinklar mellan hyperplan kan beskrivas av inre produkter av normala vektorer och hyperboliska reflektionsgrupper kan ges uttryckligen matrisförverkliganden.

I små dimensioner finns det exceptionella isomorfismer från Lie -grupper som ger ytterligare sätt att överväga symmetrier hos hyperboliska utrymmen. Till exempel i dimension 2 tillåter isomorfismen SO ⁺ (1, 2) ≅ PSL (2, R ) ≅ PSU (1, 1) en att tolka den övre halvplansmodellen som kvoten SL (2, R )/SO (2) och Poincaré -skivmodellen som kvoten SU (1, 1)/U (1) . I båda fallen verkar symmeturgrupperna genom fraktionerade linjära transformationer, eftersom båda grupperna är de orienteringsbevarande stabilisatorerna i PGL (2, C ) för respektive delutrymmen i Riemann-sfären. Cayley -transformationen tar inte bara en modell av det hyperboliska planet till det andra, utan inser symmetrigruppernas isomorfism som konjugering i en större grupp. I dimension 3 identifieras den fraktionerade linjära verkan av PGL (2, C ) på Riemann-sfären med verkan på den konformala gränsen för hyperboliskt 3-rymd inducerad av isomorfismen O ⁺ (1, 3) ≅ PGL (2, C ) . Detta gör att man kan studera isometrier av hyperboliskt 3-rymd genom att överväga spektrala egenskaper hos representativa komplexa matriser. Till exempel är paraboliska transformationer konjugerade till styva översättningar i den övre halvrumsmodellen, och de är exakt de transformationer som kan representeras av unipotenta övre triangulära matriser.

Se även

Anteckningar

Referenser

A'Campo, Norbert och Papadopoulos, Athanase, (2012) Anteckningar om hyperbolisk geometri , i: Strasbourg Master class on Geometry, s. 1–182, IRMA Lectures in Mathematics and Theoretical Physics, Vol. 18, Zürich: European Mathematical Society (EMS), 461 sidor, SBN ISBN 978-3-03719-105-7 , DOI 10.4171/105.
Coxeter, HSM , (1942) Icke-euklidisk geometri , University of Toronto Press, Toronto
Fenchel , Werner (1989). Elementär geometri i hyperboliskt utrymme . De Gruyter Matematikstudier. 11 . Berlin-New York: Walter de Gruyter & Co.
Fenchel , Werner ; Nielsen, Jakob (2003). Asmus L. Schmidt (red.). Diskontinuerliga grupper av isometrier i det hyperboliska planet . De Gruyter Matematikstudier. 29 . Berlin: Walter de Gruyter & Co.
Lobachevsky, Nikolai I., (2010) Pangeometry , redigerad och översatt av Athanase Papadopoulos, Heritage of European Mathematics, Vol. 4. Zürich: European Mathematical Society (EMS). xii, 310 ~ p, ISBN 978-3-03719-087-6 /hbk
Milnor, John W. , (1982) Hyperbolisk geometri: De första 150 åren , Bull. Amer. Matematik. Soc. (NS) Volym 6, nummer 1, s. 9–24.
Reynolds, William F., (1993) Hyperbolic Geometry on a Hyperboloid , American Mathematical Monthly 100: 442–455.
Stillwell, John (1996). Källor till hyperbolisk geometri . Matematikens historia. 10 . Providence, RI: American Mathematical Society . ISBN 978-0-8218-0529-9. MR 1402697 .
Samuels, David, (mars 2006) Knit Theory Discover Magazine, volym 27, nummer 3.
James W. Anderson, Hyperbolic Geometry , Springer 2005, ISBN 1-85233-934-9
James W. Cannon, William J. Floyd, Richard Kenyon och Walter R. Parry (1997) Hyperbolic Geometry , MSRI Publications, volym 31.

externa länkar

Javascript freeware för att skapa skisser i Poincaré Disk Model av Hyperbolic Geometry University of New Mexico
"The Hyperbolic Geometry Song" En kort musikvideo om grunderna i Hyperbolic Geometry tillgänglig på YouTube.
"Lobachevskii geometry" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
Weisstein, Eric W. "Gauss – Bolyai – Lobachevsky Space" . MathWorld .
Weisstein, Eric W. "Hyperbolic Geometry" . MathWorld .
Mer om hyperbolisk geometri, inklusive filmer och ekvationer för konvertering mellan de olika modellerna University of Illinois at Urbana-Champaign
Hyperboliska Voronoi -diagram på ett enkelt sätt, Frank Nielsen
Stothers, Wilson (2000). "Hyperbolisk geometri" . University of Glasgow . Cite journal kräver |journal=( hjälp ) , interaktiv instruktionssajt.
Hyperboliska plana tesselationer
Modeller av Hyperbolic Plane

Languages

In other projects