Lika temperament - Equal temperament
Ett lika temperament är ett musikaliskt temperament eller stämningssystem , som närmar sig bara intervall genom att dela en oktav (eller annat intervall) i lika stora steg. Detta innebär förhållandet mellan frekvenserna av någon intilliggande par av sedlar är densamma, som ger en jämn upplevda stegstorlek som tonhöjd uppfattas ungefär som logaritmen av frekvensen.
I klassisk musik och västerländsk musik i allmänhet har det vanligaste stämningssystemet sedan 1700-talet varit tolvtonat lika temperament (även känt som 12 lika temperament , 12-TET eller 12-ET ; informellt förkortat till tolv lika ), som delar oktaven i 12 delar, som alla är lika på en logaritmisk skala , med ett förhållande lika med den 12: e roten av 2 ( 12 √ 2 ≈ 1.05946). Det resulterande minsta intervallet, 1 / 12 bredden på en oktav, kallas ett halvton eller halvsteg. I västländer betyder termen lika temperament , utan kvalifikation, i allmänhet 12-TET.
I modern tid är 12-TET vanligtvis inställd i förhållande till en standardhöjd på 440 Hz, kallad A440 , vilket betyder att en ton, A , är inställd på 440 hertz och alla andra toner definieras som några multipel av halvtoner bortsett från den, antingen högre eller lägre i frekvens . Standardhöjden har inte alltid varit 440 Hz. Det har varierat och i allmänhet ökat under de senaste hundra åren.
Andra lika temperament delar oktaven olika. Till exempel har viss musik skrivits i 19-TET och 31-TET , medan det arabiska tonsystemet använder 24-TET.
I stället för att dela en oktav kan ett lika temperament också dela upp ett annat intervall, som den jämntempererade versionen av Bohlen – Pierce-skalan , som delar det rättvisa intervallet mellan en oktav och en femte (förhållande 3: 1), kallat en " tritave "eller en" pseudo-oktav "i det systemet, i 13 lika stora delar.
För inställningssystem som delar oktaven lika, men inte är approximationer av bara intervall, kan termen lika uppdelning av oktav eller EDO användas.
Ofrettade strängensembler , som kan justera stämningen av alla noter utom öppna strängar och sånggrupper, som inte har några mekaniska inställningsbegränsningar, använder ibland en inställning mycket närmare just intonation av akustiska skäl. Andra instrument, till exempel en del vind- , tangentbord- och fretted -instrument, är ofta bara ungefärliga lika temperament, där tekniska begränsningar förhindrar exakta inställningar. Vissa blåsinstrument som enkelt och spontant kan böja sin ton, framför allt tromboner , använder stämning som liknar strängensembler och sånggrupper.
Generella egenskaper
I ett lika temperament är avståndet mellan två angränsande steg i vågen samma intervall . Eftersom den upplevda identiteten för ett intervall beror på dess förhållande är denna skala i jämna steg en geometrisk sekvens av multiplikationer. (En aritmetisk sekvens av intervall låter inte jämnt fördelat och tillåter inte transponering till olika nycklar.) Specifikt är det minsta intervallet i en jämntempererad skala förhållandet:
där förhållandet r delar förhållandet p (vanligtvis oktaven , som är 2: 1) i n lika stora delar. ( Se tolvtonas lika temperament nedan. )
Skalor mäts ofta i cent , som delar oktaven i 1200 lika stora intervall (var och en kallas en cent). Denna logaritmiska skala gör jämförelse av olika inställningssystem enklare än att jämföra förhållanden och har stor användning inom etnomusikologi . Det grundläggande steget i cent för alla lika temperament kan hittas genom att ta bredden p ovan i cent (vanligtvis oktaven, som är 1200 cent bred), kallad nedan w , och dela den i n delar:
I musikalisk analys ges material som tillhör ett lika temperament ofta ett heltal , vilket betyder att ett enda heltal används för att representera varje tonhöjd. Detta förenklar och generaliserar diskussionen om tonhöjdsmaterial inom temperamentet på samma sätt som att ta logaritmen för en multiplikation reducerar det till addition. Genom att tillämpa den modulära aritmetiken där modulen är antalet oktavindelningar (vanligtvis 12) kan dessa heltal reduceras till tonhöjdsklasser , vilket tar bort distinktionen (eller erkänner likheten) mellan tonhöjd med samma namn, t.ex. c är 0 oavsett oktavregister. Den MIDI kodningsstandard användningsområden heltal not beteckningar.
Allmänna formler för det jämntempererade intervallet
Tolvtoners lika temperament
12-ton lika temperament, som delar oktaven i tolv lika stora intervall, är det vanligaste musiksystemet som används idag, särskilt i västerländsk musik.
Historia
De två siffror som ofta krediteras för att uppnå exakt beräkning av lika temperament är Zhu Zaiyu (även romaniserad som Chu-Tsaiyu. Kinesiska:朱 載 堉) 1584 och Simon Stevin 1585. Enligt Fritz A. Kuttner, kritiker av teori, är det känt att "Chu-Tsaiyu presenterade en mycket exakt, enkel och genial metod för aritmetisk beräkning av mono-ackord med lika temperament 1584" och att "Simon Stevin erbjöd en matematisk definition av lika temperament plus en något mindre exakt beräkning av motsvarande numeriska värden 1585 eller senare. " Utvecklingen skedde självständigt.
Kenneth Robinson tillskriver uppfinningen av lika temperament till Zhu Zaiyu och tillhandahåller textcitat som bevis. Zhu Zaiyu citeras för att säga att i en text från 1584, "Jag har grundat ett nytt system. Jag fastställer en fot som det tal från vilket de andra ska extraheras, och med hjälp av proportioner extraherar jag dem. Sammantaget måste man hitta de exakta siffrorna för pitch-pipers i tolv operationer. " Kuttner håller inte med och påpekar att hans påstående "inte kan anses korrekt utan större kvalifikationer". Kuttner föreslår att varken Zhu Zaiyu eller Simon Stevin uppnådde lika temperament och att ingen av de två ska behandlas som uppfinnare.
Kina
Medan Kina tidigare hade kommit med approximationer för 12-TET, var Zhu Zaiyu den första personen som matematiskt löste tolvtona lika temperament, vilket han beskrev i sin Fusion of Music and Calendar 律 暦 融通1580 och Complete Compendium of Music and Pitch ( Yuelü quan shu 樂 律 全書) år 1584. Ett utökat konto lämnas också av Joseph Needham. Zhu fick sitt resultat matematiskt genom att dela strängens och rörets längd successivt med 12 √ 2 ≈ 1.059463, och för rörlängden med 24 √ 2 , så att efter tolv divisioner (en oktav) delades längden med en faktor 2.
Zhu Zaiyu skapade flera instrument anpassade till hans system, inklusive bambu rör.
Europa
Några av de första européerna som förespråkade ett lika temperament var lutenisterna Vincenzo Galilei , Giacomo Gorzanis och Francesco Spinacino , som alla skrev musik i den.
Simon Stevin var den första som utvecklade 12-TET baserat på den tolfte roten av två , som han beskrev i Van De Spiegheling der singconst (ca 1605), publicerad postuum nästan tre århundraden senare 1884.
I flera århundraden använde Europa en mängd olika stämningssystem, inklusive 12 lika temperament, liksom ett enda temperament och ett bra temperament , som alla kan ses som en approximation av det förra. Plockade instrumentspelare (lutenister och gitarristar) gynnade i allmänhet lika temperament, medan andra var mer splittrade. Till slut vann tolvtona lika temperament. Detta tillät nya stilar av symmetrisk tonalitet och polytonalitet , atonal musik som den som skrevs med tolvtonstekniken eller serialismen , och jazz (åtminstone dess pianokomponent) utvecklades och blomstrade.
Matematik
I tolvtoners lika temperament, som delar oktaven i 12 lika delar, är halvtonens bredd , det vill säga frekvensförhållandet för intervallet mellan två intilliggande toner, den tolfte roten av två :
Detta motsvarar:
Detta intervall är uppdelat i 100 cent .
Beräkning av absoluta frekvenser
För att hitta frekvensen, P n , för en anteckning i 12-TET kan följande definition användas:
I denna formel refererar P n till tonhöjden eller frekvensen (vanligtvis i hertz ) som du försöker hitta. P a hänför sig till frekvensen hos en referenstonen. n och en hänvisning till nummer som tilldelats önskad tonhöjd respektive referenshöjd. Dessa två nummer är från en lista med på varandra följande heltal som tilldelats på varandra följande halvtoner. Till exempel är A 4 (referenshöjden) den 49: e tangenten från ett pianos vänstra ände (inställd på 440 Hz ) och C 4 ( mitt C ), och F# 4 är den 40: e respektive 46: e tangenten. Dessa nummer kan användas för att hitta frekvensen för C 4 och F# 4 :
Omvandla frekvenser till sina likvärdiga temperamentmotparter
För att konvertera en frekvens (i Hz) till dess likvärdiga 12-TET-motsvarighet kan följande formel användas:
Där E n hänvisar till frekvensen för en stigning i lika temperament, och en hänför sig till frekvensen hos en referenstonen. Till exempel, (om vi låter referenshöjden vara 440 Hz) kan vi se att E 5 och C# 5 är lika med följande frekvenser:
Jämförelse med bara intonation
Intervallen på 12-TET närmar sig vissa intervall nära just intonation . Den femtedel och den fjärde är nästan oskiljbart nära bara intervall, medan tredjedelar och sjätte är längre bort.
I följande tabell jämförs storleken på olika rättvisa intervall med sina likvärdiga motsvarigheter, såväl i förhållande som cent .
| Intervallnamn | Exakt värde i 12-TET | Decimalvärde i 12-TET | Cent | Bara intonationsintervall | Cent i bara intonation | Skillnad |
|---|---|---|---|---|---|---|
| Unison ( C ) | 2 0 ⁄ 12 = 1 | 1 | 0 | 1 ⁄ 1 = 1 | 0 | 0 |
| Augmented unison / Minor second ( C ♯ / D ♭ ) | 2 1 ⁄ 12 = 12 √ 2 | 1.059463 | 100 | 16 ⁄ 15 = 1,066 ... | 111,73 | -11,73 |
| Major andra ( D ) | 2 2 ⁄ 12 = 6 √ 2 | 1.122462 | 200 | 9 ⁄ 8 = 1,125 | 203,91 | -3,91 |
| Augmented second / Mindre tredje ( D ♯ / E ♭ ) | 2 3 ⁄ 12 = 4 √ 2 | 1.189207 | 300 | 6 ⁄ 5 = 1,2 | 315,64 | -15,64 |
| Major tredjedel ( E ) | 2 4 ⁄ 12 = 3 √ 2 | 1.259921 | 400 | 5 ⁄ 4 = 1,25 | 386,31 | +13,69 |
| Perfekt fjärde ( F ) | 2 5 ⁄ 12 = 12 √ 32 | 1.33484 | 500 | 4 ⁄ 3 = 1,33333 ... | 498,04 | +1,96 |
| Triton ( F ♯ / G ♭ ) | 2 6 ⁄ 12 = √ 2 | 1.414214 | 600 | 64 ⁄ 45 = 1,422 ... | 609,78 | -9,78 |
| Perfekt femte ( G ) | 2 7 ⁄ 12 = 12 √ 128 | 1.498307 | 700 | 3 ⁄ 2 = 1,5 | 701,96 | -1,96 |
| Förstorad femte / mindre sjätte ( G ♯ / A ♭ ) | 2 8 ⁄ 12 = 3 √ 4 | 1.587401 | 800 | 8 ⁄ 5 = 1,6 | 813,69 | -13,69 |
| Major sjätte ( A ) | 2 9 ⁄ 12 = 4 √ 8 | 1.681793 | 900 | 5 ⁄ 3 = 1.66666 ... | 884,36 | +15,64 |
| Förstorad sjätte / mindre sjunde ( A ♯ / B ♭ ) | 2 10 ⁄ 12 = 6 √ 32 | 1.781797 | 1000 | 16 ⁄ 9 = 1.77777 ... | 996,09 | +3,91 |
| Major sjunde ( B ) | 2 11 ⁄ 12 = 12 √ 2048 | 1.887749 | 1100 | 15 ⁄ 8 = 1,875 | 1088.270 | +11,73 |
| Oktav ( C ) | 2 12 ⁄ 12 = 2 | 2 | 1200 | 2 ⁄ 1 = 2 | 1200,00 | 0 |
Sju toners lika uppdelning av den femte
Fioler, fioler och cellor är avstämda i perfekta femtedelar (G-D-A-E, för fioler och C-G-D-A, för fiol och cellor), vilket tyder på att deras halvtonförhållande är något högre än i det konventionella tolvtoniga lika temperamentet. Eftersom en perfekt femtedel är i 3: 2 -relation med sin grundton, och detta intervall täcks i 7 steg, är varje ton i förhållandet 7 √ 3 ⁄ 2 till nästa (100,28 cent), vilket ger en perfekt femtedel med förhållandet 3: 2 men en något vidgad oktav med förhållandet ≈ 517: 258 eller ≈ 2.00388: 1 snarare än det vanliga 2: 1 -förhållandet, eftersom tolv perfekta femtedelar inte motsvarar sju oktaver. Under själva spelet väljer violinisten dock platser efter örat, och endast de fyra oavbrutna tonhöjden i strängarna kommer garanterat att uppvisa detta 3: 2 -förhållande.
Andra lika temperament
5 och 7 toniga temperament i etnomusikologi
Fem och sju ton lika temperament ( 5-TET Play ( hjälp · info ) och 7-TET Play ( hjälp · info ) ), med 240 Play ( hjälp · info ) och 171 Play ( hjälp · info ) cent steg, är rättvist allmänning.
![]()
![]()
![]()
![]()
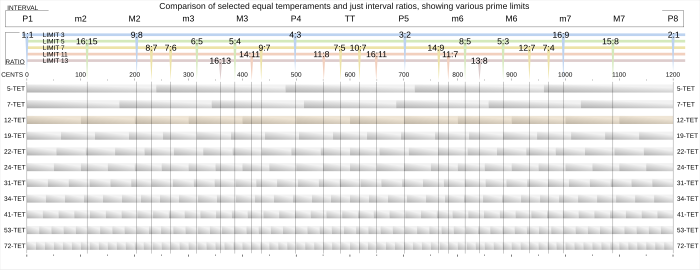
5-TET och 7-TET markerar slutpunkterna för det syntoniska temperamentets giltiga inställningsområde, som visas i figur 1 .
- I 5-TET är den härdade perfekta femtan 720 cent bred (högst upp på tuningkontinuumet) och markerar slutpunkten på tuningkontinuum vid vilken bredden på den mindre sekunden krymper till en bredd av 0 cent.
- I 7-TET är den härdade perfekta femman 686 cent bred (längst ner i stämningskontinuumet) och markerar slutpunkten på stämningskontinuumet, där den mindre sekunden expanderar till att vara lika bred som den stora sekunden (vid 171 cent vardera ).
5-ton lika temperament
Indonesiska gamelans är inställda på 5-TET enligt Kunst (1949), men enligt Hood (1966) och McPhee (1966) varierar deras inställning mycket och enligt Tenzer (2000) innehåller de sträckta oktaver . Det är nu väl accepterat att av de två primära stämningssystemen inom gamelanmusik, slendro och pelog , liknar endast slendro något femtonigt lika temperament medan pelog är mycket ojämlikt; Surjodiningrat et al. (1972) har analyserat pelog som en delmängd av sju toner av nioton lika temperament (133 cent steg Play ( hjälp · info ) ).
![]()
7-tonat lika temperament
En thailändsk xylofon mätt av Morton (1974) "varierade bara plus minus 5 cent", från 7-TET. Enligt Morton, "thailändska instrument med fast tonhöjd är inställda på ett likvidistiskt system med sju tonhöjd per oktav ... Liksom i västerländsk traditionell musik används dock inte alla tonhöjden i stämningssystemet i ett läge (kallas ofta ' skala '); i det thailändska systemet används fem av de sju i huvudsakliga tonhöjd i vilket läge som helst, och därmed upprättas ett mönster med icke -avståndsintervaller för läget. " Spela ( hjälp · info )![]()
En sydamerikansk indisk skala från en preinstrumental kultur uppmätt av Boiles (1969) innehöll 175 cent sju ton lika temperament, vilket sträcker oktaven något som med instrumental gamelan musik.
Kinesisk musik har traditionellt använt 7-TET.
Olika lika temperament

24 EDO , kvarttontonskalan (eller 24-TET), var en populär mikrotonal stämning på 1900-talet förmodligen för att den representerade en bekväm åtkomstpunkt för kompositörer betingade av standard Western 12 EDO-tonhöjd och notationsmetoder som också var intresserade av mikrotonalitet. Eftersom 24 EDO innehåller alla tonhöjden på 12 EDO, plus nya platser halvvägs mellan varje angränsande par med 12 EDO-platser, kan de använda de extra färgerna utan att förlora någon taktik som finns tillgänglig i 12-tonars harmoni. Det faktum att 24 är en multipel av 12 gjorde också 24 EDO lätt att uppnå instrumentellt genom att använda två traditionella 12 EDO-instrument som avsiktligt stämde in en kvartton från varandra, till exempel två pianon, vilket också gjorde det möjligt för varje artist (eller en artist som spelar ett annat piano) med varje hand) för att läsa välkänd 12-tonig notation. Olika kompositörer inklusive Charles Ives experimenterade med musik för kvartstoner. 24 EDO närmar sig den elfte övertonen mycket bra, till skillnad från 12 EDO.
19 EDO är känt och vissa instrument är stämda i 19 EDO. Den har något plattare perfekta femtedel (vid 695 cent), men dess största sjätte är mindre än en enda cent från just intonations största sjätte (vid 884 cent). Dess mindre tredjedel är också mindre än en cent från bara intonationer. (Den lägsta EDO som ger en bättre mindre trea och major sjätte än 19 EDO är 232 EDO.) Dess perfekta fjärde (vid 505 cent) är bara 5 cent skarp än bara intonationer och 3 cent skarpa från 12-tet.
23 EDO är den största EDO som inte når ungefär 3: e, 5: e, 7: e och 11: e övertonen (3: 2, 5: 4, 7: 4, 11: 8) inom 20 cent, vilket gör den attraktiv för mikrotonalister som letar efter ovanliga mikrotoner harmoniskt territorium.
26 EDO är den minsta EDO som nästan rent avstämmer den 7: e övertonen (7: 4). Det är också ett mycket platt temperament som betyder att efter 4 femtedelar ger det en neutral 3: e snarare än en stor. 26 EDO har två mindre tredjedelar och två mindre sjättedelar. Det kan vara lite förvirrande vid första anblicken för om du spelar den neutrala 3: e låter det som en väldigt platt major. 26EDO kan vara ett alternativt temperament för Barbershop -harmoni.
27 EDO är den minsta EDO som unikt representerar alla intervall med de första åtta övertonerna. Det dämpar septimalkommat men inte det syntoniska komma .
29 EDO är det lägsta antalet lika delar av oktaven som ger en bättre perfekt femma än 12 EDO. Dess största tredjedel är ungefär lika felaktig som 12-TET; den är dock inställd 14 cent platt istället för 14 cent skarp. Den stämmer också den 7: e, 11: e och 13: e övertonen platt, ungefär lika mycket. Detta innebär att intervaller som 7: 5, 11: 7, 13:11, etc., alla matchar extremt bra i 29-TET.
31 EDO förespråkades av Christiaan Huygens och Adriaan Fokker . 31 EDO har en något mindre exakt femma än 12 EDO, men ger nästan bara stora tredjedelar och ger anständiga matchningar för övertoner upp till minst 13, varav den sjunde övertonen är särskilt exakt.
34 EDO ger något mindre totala kombinerade fel av approximation till 5-gränsen bara förhållanden 3: 2, 5: 4, 6: 5, och deras inversioner än 31 EDO gör, även om approximationen av 5: 4 är sämre. 34 EDO uppskattar inte förhållanden med primär 7 -brunn. Den innehåller en 600-cent triton, eftersom det är en jämn EDO.
41 EDO är det näst lägsta antalet lika divisioner som ger en bättre perfekt femma än 12 EDO. Dess största tredjedel är mer exakt än 12 EDO och 29 EDO, cirka 6 cent platt. Det är inte menat, så det skiljer 10: 9 och 9: 8, till skillnad från 31edo. Det är mer exakt i 13-gräns än 31edo.
46 EDO ger något vassa större tredjedelar och perfekta femtedelar, vilket ger triader ett karakteristiskt starkt ljud. Övertonerna upp till 11 approximeras inom 5 cent av noggrannhet, med 10: 9 och 9: 5 som en femtedel av centen från ren. Eftersom det inte är ett menat system, skiljer det 10: 9 och 9: 8.
53 EDO är bättre på att närma sig de traditionella rättvisa konsonanserna än 12, 19 eller 31 EDO, men har endast använts en och annan gång. Dess extremt bra perfekta femtedel gör det utbytbart med en utökad Pythagoras stämning , men det rymmer också schismatiskt temperament och används ibland i turkisk musikteori. Det uppfyller dock inte kraven i ett temperament, som sätter goda tredjedelar inom räckhåll via femtedelscykeln. I 53 EDO skulle mycket konsonant tredjedelar nås i stället med hjälp av en Pythagorean minskad fjärde (CF ♭ ), eftersom det är ett exempel på schismatiskt temperament , precis som 41 EDO.
72 EDO närmar sig många precis intonationsintervaller väl, även in i 7-gränsen och 11-gränsen, till exempel 7: 4, 9: 7, 11: 5, 11: 6 och 11: 7. 72 EDO har undervisats, skrivits och utförts i praktiken av Joe Maneri och hans elever (vars atonala böjelser vanligtvis undviker någon hänvisning till just intonation alls). Det kan betraktas som en förlängning av 12 EDO eftersom 72 är en multipel av 12. 72 EDO har ett minsta intervall som är sex gånger mindre än det minsta intervallet på 12 EDO och därför innehåller sex kopior av 12 EDO som börjar på olika platser. Den innehåller också tre kopior av 24 EDO och två kopior av 36 EDO, som själva är multiplar av 12 EDO. 72 EDO har också kritiserats för sin redundans genom att behålla de dåliga approximationerna i 12 EDO, trots att de inte behövdes för några lägre gränser för just intonation (t.ex. 5-gräns).
96 EDO närmar sig alla intervall inom 6,25 cent, vilket knappt går att urskilja. Som en åttafaldig multipel av 12 kan den användas fullt ut som den vanliga 12 EDO. Det har förespråkats av flera kompositörer, särskilt Julián Carrillo från 1924 till 1940 -talet.
Andra lika uppdelningar av oktaven som hittat tillfällig användning inkluderar 15 EDO , 17 EDO och 22 EDO .
2, 5, 12, 41, 53, 306, 665 och 15601 är nämnare för de första konvergenterna i log 2 (3), så 2, 5, 12, 41, 53, 306, 665 och 15601 tolfdelar (och femtedelar), är i korrespondent är lika temperament lika med ett heltal oktaver bättre approximation av 2, 5, 12, 41, 53, 306, 665 och 15601 bara tolfdelar/femtedelar än för alla lika temperament med färre toner.
1, 2, 3, 5, 7, 12, 29, 41, 53, 200 ... (sekvens A060528 i OEIS ) är sekvensen av oktavindelningar som ger bättre och bättre approximationer av den perfekta femman. Relaterade sekvenser innehåller divisioner som approximerar andra bara intervall.
Denna applikation: [1] beräknar frekvenser, ungefärliga cent och MIDI -böjvärden för alla system med lika uppdelning av oktav. Observera att 'rundade' och 'golvade' ger samma MIDI -böjningsvärde.
Lika temperament med icke-oktavintervall
Den jämntempererade versionen av Bohlen – Pierce-skalan består av förhållandet 3: 1, 1902 cent, konventionellt en perfekt femma plus en oktav (det vill säga en perfekt tolfte), som i denna teori kallas tritave ( play ( hjälp · info) ) ) och delas upp i tretton lika delar. Detta ger en mycket nära matchning till just avstämda förhållanden som endast består av udda tal. Varje steg är 146,3 cent ( spela ( hjälp · info ) ) eller 13 √ 3 .
![]()
![]()
Wendy Carlos skapade tre ovanliga lika temperament efter en grundlig studie av egenskaperna hos möjliga temperament med en stegstorlek mellan 30 och 120 cent. Dessa kallades alfa , beta och gamma . De kan betraktas som lika delar av den perfekta femman. Var och en av dem ger en mycket bra approximation av flera bara intervaller. Deras stegstorlekar:
-
alfa : 9 √ 3 ⁄ 2 (78,0 cent) Spela ( hjälp · info )

-
beta : 11 √ 3 ⁄ 2 (63,8 cent) Spela ( hjälp · info )

-
gamma : 20 √ 3 ⁄ 2 (35,1 cent) Spela ( hjälp · info )

Alpha och Beta kan höras på titelspåret på hennes 1986 album i skönheten .
Proportioner mellan halvton och hel ton
I detta avsnitt kanske halvton och hel ton inte har sina vanliga 12-EDO-betydelser, eftersom det diskuterar hur de kan tempereras på olika sätt från sina rättvisa versioner för att skapa önskade relationer. Låt antalet steg i en halvton vara s , och antalet steg i en ton vara t .
Det finns exakt en familj med lika temperament som fixar halvtonen till en lämplig bråkdel av en hel ton, samtidigt som tonerna hålls i rätt ordning (vilket betyder att till exempel C, D, E, F och F ♯ är i stigande ordning om de bevarar sina vanliga förhållanden till C). Det vill säga att fixera q till en ordentlig bråkdel i relationen qt = s definierar också en unik familj med ett lika temperament och dess multiplar som uppfyller detta förhållande.
Till exempel, där k är ett heltal, 12 k -EDO -uppsättningar q = 1 ⁄ 2 och 19 k -EDO -uppsättningar q = 1 ⁄ 3 . De minsta multiplarna i dessa familjer (t.ex. 12 och 19 ovan) har den extra egenskapen att de inte har några anteckningar utanför cirkeln av femtedelar . (Detta är inte sant i allmänhet; i 24-EDO är halvskarpen och halvlägena inte i cirkeln av femtedelar som genereras från C.) Extrema fall är 5 k -EDO, där q = 0 och halvtonen blir en unison, och 7 k -EDO, där q = 1 och halvtonen och tonen är samma intervall.
När man väl vet hur många steg en halvton och en ton har i detta lika temperament, kan man hitta antalet steg den har i oktaven. Ett lika temperament som uppfyller ovanstående egenskaper (inklusive att ha inga noter utanför cirkeln av femtedelar) delar oktaven i 7 t - 2 s steg och den perfekta femman i 4 t - s steg. Om det finns anteckningar utanför cirkeln av femtedelar, måste man sedan multiplicera dessa resultat med n , vilket är antalet icke-överlappande cirklar av femtedelar som krävs för att generera alla anteckningar (t.ex. två i 24-EDO, sex i 72-EDO). (Man måste ta den lilla halvton för detta syfte: 19-EDO har två halvtoner, varav ett är en / 3 ton och den andra varelse 2 / 3 .)
Den minsta av dessa familjer är 12 k -EDO, och i synnerhet 12 -EDO är det minsta lika temperament som har ovanstående egenskaper. Dessutom gör det också halvtonen exakt till en halv hel ton, det enklaste möjliga förhållandet. Detta är några av anledningarna till att 12-EDO har blivit det vanligaste lika temperamentet. (En annan anledning är att 12-EDO är det minsta lika temperamentet för att nästan närma sig 5-gränss harmoni, den näst minsta är 19-EDO.)
Varje val av bråk q för förhållandet resulterar i exakt en lika temperamentsfamilj, men det motsatta är inte sant: 47-EDO har två olika halvtoner, där den ena är 1 ⁄ 7 ton och den andra är 8 ⁄ 9 , vilket inte är komplement av varandra som i 19-EDO ( 1 ⁄ 3 och 2 ⁄ 3 ). Att ta varje halvton resulterar i ett annat val av perfekt femma.
Relaterade inställningssystem
Regelbundna diatoniska inställningar

Den diatoniska inställningen i tolv lika kan generaliseras till vilken vanlig diatonisk inställning som helst som delar oktaven som en sekvens av steg TTSTTTS (eller en rotation av den) med alla T: erna och alla S: erna i samma storlek och S: n mindre än T: erna. I tolv lika är S halvtonen och är exakt halva storleken på tonen T. När S: n reduceras till noll är resultatet TTTTT eller ett femton lika temperament, När halvtonerna blir större blir slutligen alla steg lika storlek, och resultatet är i sju ton lika temperament. Dessa två slutpunkter ingår inte som vanliga diatoniska inställningar.
Noterna i en vanlig diatonisk stämning är sammankopplade med en cykel på sju härdade femtedelar. Tolvtonarsystemet generaliserar på liknande sätt till en sekvens CDCDDCDCDCDD (eller en rotation av det) av kromatiska och diatoniska halvtoner som är sammanlänkade i en cykel av tolv femtedelar. I detta fall erhålls sju lika i gränsen eftersom storleken på C tenderar till noll och fem lika är gränsen då D tenderar till noll medan tolv lika är naturligtvis fallet C = D.
Några av mellanstorlekarna för toner och halvtoner kan också genereras i system med lika temperament. Till exempel om den diatoniska halvtonen är dubbelt så stor som den kromatiska halvtonen, dvs D = 2*C är resultatet nitton lika med ett steg för den kromatiska halvtonen, två steg för den diatoniska halvtonen och tre steg för tonen och det totala antalet av steg 5*T + 2*S = 15 + 4 = 19 steg. Det resulterande tolvtoniga systemet närmar sig nära det historiskt viktiga 1/3-kommatonet.
Om den kromatiska halvtonen är två tredjedelar av storleken på den diatoniska halvtonen, dvs C = (2/3)*D, blir resultatet trettio lika, med två steg för den kromatiska halvtonen, tre steg för den diatoniska halvtonen, och fem steg för tonen där 5*T + 2*S = 25 + 6 = 31 steg. Det resulterande tolvtoniga systemet närmar sig nära den historiskt viktiga 1/4 komma-mellantonen.
Se även
- Bara intonation
- Musikalisk akustik (musikens fysik)
- Musik och matematik
- Mikrotuner
- Mikrotonal musik
- Pianostämning
- Lista över mellandelsintervaller
- Diatoniskt och kromatiskt
- Elektronisk tuner
- Musikalisk stämning
Referenser
Citat
Källor
- Cho, Gene Jinsiong. (2003). Upptäckten av musikaliskt jämnt temperament i Kina och Europa under sextonde århundradet . Lewiston, NY: Edwin Mellen Press .
- Duffin, Ross W. Hur jämnt temperament förstörde harmoni (och varför du borde bry dig) . WWNorton & Company, 2007.
- Jorgensen, Owen. Tuning . Michigan State University Press, 1991. ISBN 0-87013-290-3
- Sethares, William A. (2005). Tuning, Timbre, Spectrum, Scale (andra upplagan). London: Springer-Verlag. ISBN 1-85233-797-4.
- Surjodiningrat, W., Sudarjana, PJ och Susanto, A. (1972) Tonmätningar av enastående javanesiska gamelans i Jogjakarta och Surakarta , Gadjah Mada University Press, Jogjakarta 1972. Citerat på https://web.archive.org/web/ 20050127000731/http: //web.telia.com/~u57011259/pelog_main.htm . Hämtad 19 maj 2006.
- Stewart, PJ (2006) "From Galaxy to Galaxy: Music of the Spheres" [2]
- Khramov, Mykhaylo. "Approximation of 5-limit just intonation. Computer MIDI Modeling in Negative Systems of Equal Divisions of Octave", Proceedings of the International Conference SIGMAP-2008 , 26–29 juli 2008, Porto , s. 181–184, ISBN 978-989 -8111-60-9
Vidare läsning
- Sensations of Tone ett grundläggande arbete om akustik och ljuduppfattning av Hermann von Helmholtz. Speciellt bilaga XX: Översättarens tillägg, sid 430-556, (pdf sid 451-577)]
externa länkar
- Xenharmonic wiki om EDO vs. jämna temperaturer
- Huygens-Fokker Foundation Center för mikrotonal musik
- A.Orlandini: Musikakustik
- "Temperament" från ett tillägg till Mr. Chambers's cyclopædia (1753)
- Barbieri, Patrizio. Enharmoniska instrument och musik, 1470–1900 . (2008) Latina, Il Levante Libreria Editrice
- Fraktal mikrotonal musik , Jim Kukula .
- Alla befintliga 1700 -tals citat om JS Bach och temperament
- Dominic Eckersley: " Rosetta Revisited: Bachs mycket vanliga temperament "
- Well Temperaments, baserat på Werckmeister Definition
- F AVORED C ARDINALITIES O F S CALES av P ETER B UCH



![{\ displaystyle r = {\ sqrt [{n}] {p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b55fb394d767c50fb569ca27fd636072c72fbd7c)



![{\ displaystyle {\ sqrt [{12}] {2}} = 2^{\ frac {1} {12}} \ ca 1.059463}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232c2beab28b1c46c328080d982595d9ef196e08)

![{\ displaystyle P_ {n} = P_ {a} \ vänster ({\ sqrt [{12}] {2}} \ höger)^{(na)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3381e111c79f7e16a073bbe05c6cabeaba2ff79a)
![{\ displaystyle P_ {40} = 440 \ vänster ({\ sqrt [{12}] {2}} \ höger)^{(40-49)} \ approx 261.626 \ \ mathrm {Hz}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f16dc9af5bbe778786f73eca304c80c72584cd70)
![{\ displaystyle P_ {46} = 440 \ vänster ({\ sqrt [{12}] {2}} \ höger)^{(46-49)} \ ca 369.994 \ \ mathrm {Hz}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7144b8e3148077acb97a47d384a62a1f2a5445)



