Oddsförhållande - Odds ratio

Ett oddskvot ( OR ) är en statistik som kvantifierar styrkan i sambandet mellan två händelser, A och B. Oddskvoten definieras som förhållandet mellan oddsen för A i närvaro av B och oddsen för A i frånvaro av B, eller motsvarande (på grund av symmetri ), förhållandet mellan oddsen för B i närvaro av A och oddsen för B i frånvaro av A. Två händelser är oberoende om och bara om OR är lika med 1, dvs. oddsen för en händelse är desamma antingen i närvaro eller frånvaro av den andra händelsen. Om OR är större än 1, är A och B associerade (korrelerade) i den meningen att närvaron av B ökar oddsen för A, och symmetriskt närvaron av A ökar oddsen för B Om motsatsen däremot är mindre än 1, korreleras A och B negativt och närvaron av en händelse minskar oddsen för den andra händelsen.

Observera att oddskvoten är symmetrisk i de två händelserna och att det inte finns någon kausal riktning ( korrelation innebär inte orsakssamband ): en ELLER större än 1 visar inte att B orsakar A eller att A orsakar B.

Två liknande statistik som ofta används för att kvantifiera associationer är riskförhållandet (RR) och den absoluta riskminskningen (ARR). Ofta är parametern av störst intresse faktiskt RR, vilket är förhållandet mellan sannolikheterna analoga med oddsen som används i OR. Tillgängliga data tillåter emellertid ofta inte beräkning av RR eller ARR men möjliggör beräkning av OR, som i fallkontrollstudier , som förklaras nedan. Å andra sidan, om en av egenskaperna (A eller B) är tillräckligt sällsynt (i epidemiologi kallas detta antagandet om sällsynt sjukdom ), så är OR ungefär lika med motsvarande RR.

OR spelar en viktig roll i den logistiska modellen .

Definition och grundläggande egenskaper

Ett motiverande exempel, i samband med antagandet om sällsynta sjukdomar

Antag att ett strålläckage i en by på 1 000 människor ökade förekomsten av en sällsynt sjukdom. Det totala antalet personer som utsattes för strålningen var av vilka utvecklade sjukdomen och förblev friska. Det totala antalet personer som inte exponerades var av vilka utvecklade sjukdomen och förblev friska. Vi kan organisera detta i en tabell : ${\ displaystyle V_ {E} = 400,}$${\ displaystyle D_ {E} = 20}$${\ displaystyle H_ {E} = 380}$${\ displaystyle V_ {N} = 600,}$${\ displaystyle D_ {N} = 6}$${\ displaystyle H_ {N} = 594}$

${\ displaystyle {\ begin {array} {| r | cc |} \ hline & {\ text {Sjuk}} & {\ text {Healthy}} \\\ hline {\ text {Exposed}} & {20} & {380} \\ {\ text {Not exposed}} & {6} & {594} \\\ hline \ end {array}}}$

Den risk att utveckla exponerings sjukdom ges är och att utveckla sjukdomen ges icke-exponering . Ett uppenbart sätt att jämföra riskerna är att använda förhållandet mellan de två, den relativa risken (ett annat sätt är att titta på den absoluta skillnaden,${\ displaystyle D_ {E}/V_ {E} = 20/400 = .05}$${\ displaystyle D_ {N}/V_ {N} = 6/600 = .01}$${\ displaystyle .05-.01 = .04).}$

${\ displaystyle Relative \; Risk = {\ frac {D_ {E}/V_ {E}} {D_ {N}/V_ {N}}} = {\ frac {20/400} {6/600}} = {\ frac {.05} {. 01}} = 5 \,}$

Oddskvoten är annorlunda. De odds att få sjukdomen om de utsätts är och oddsen om inte utsatta är den oddskvoten är förhållandet mellan de två, ${\ displaystyle D_ {E}/H_ {E} = 20/380 \ approx. 052,}$${\ displaystyle D_ {N}/H_ {N} = 6/594 \ approx .010 \ ,.}$

${\ displaystyle Odds \; Ratio = {\ frac {D_ {E}/H_ {E}} {D_ {N}/H_ {N}}} = {\ frac {20/380} {6/594}} \ ungefär {\ frac {.052} {. 010}} = 5,2 \,}$.

Som du kan se är den relativa risken och oddskvoten i det här fallet med sällsynta sjukdomar nästan lika. Per definition innebär sällsynt sjukdom att och . Således är nämnarna i det relativa risk- och oddskvoten nästan desamma ( och . ${\ displaystyle V_ {E} \ approx H_ {E}}$${\ displaystyle V_ {N} \ approx H_ {N}}$${\ displaystyle 400 \ ca 380}$${\ displaystyle 600 \ approx 594)}$

Relativ risk är lättare att förstå än oddskvoten, så varför använda oddskvoten? En anledning är att vi vanligtvis inte har data om hela befolkningen och måste använda stickprov . Antag i vårt exempel att det är mycket kostsamt att intervjua bybor och ta reda på om de utsattes för strålningen; vi har ingen aning om förekomsten av strålningsexponering, värdena på eller . Vi skulle kunna ta ett slumpmässigt urval av femtio bybor, men mycket troligtvis skulle ett sådant slumpmässigt urval inte inkludera någon med sjukdomen, eftersom endast 2,6% av befolkningen är sjuka. Istället kan vi använda en fallkontrollstudie där vi intervjuar alla 26 sjuka bybor och ett slumpmässigt urval av 26 som inte har sjukdomen. Resultaten kan bli följande ("kanske", eftersom detta är ett slumpmässigt urval): ${\ displaystyle V_ {E}}$${\ displaystyle V_ {N}}$

${\ displaystyle {\ begin {array} {| r | cc |} \ hline & {\ text {Sjuk}} & {\ text {Healthy}} \\\ hline {\ text {Exposed}} & {20} & {10} \\ {\ text {Not exposed}} & {6} & {16} \\\ hline \ end {array}}}$

Oddsen i detta prov för att få sjukdomen med tanke på att någon utsätts är 20/10 och oddsen med tanke på att någon inte utsätts är 6/16. Oddskvoten är alltså . Den relativa risken kan dock inte beräknas, eftersom det är förhållandet mellan riskerna för att få sjukdomen och vi skulle behöva och räkna ut dem. Eftersom vi valde ut för personer med sjukdomen har hälften av personerna i vårt urval sjukdomen och vi vet att det är mer än befolkningsövergripande prevalans. ${\ displaystyle {\ frac {20/10} {6/16}} \ ca 5,3}$${\ displaystyle V_ {E}}$${\ displaystyle V_ {N}}$

Det är standard i den medicinska litteraturen att beräkna oddskvoten och sedan använda antagandet om sällsynt sjukdom (som vanligtvis är rimligt) för att hävda att den relativa risken är ungefär densamma. Detta möjliggör inte bara användning av fallkontrollstudier, utan gör kontrollen för förvirrande variabler som vikt eller ålder med hjälp av regressionsanalys enklare och har de önskvärda egenskaper som diskuteras i andra avsnitt av denna artikel om invarians och okänslighet för typen av provtagning .

Definition när det gäller gruppmässiga odds

Oddskvoten är förhållandet mellan oddsen för en händelse som inträffar i en grupp och oddsen för att den ska inträffa i en annan grupp. Termen används också för att referera till stickprovsbaserade uppskattningar av detta förhållande. Dessa grupper kan vara män och kvinnor, en experimentell grupp och en kontrollgrupp eller någon annan dikotom klassificering. Om sannolikheten för händelsen i var och en av grupperna är p ₁ (första gruppen) och p ₂ (andra gruppen), är oddskvoten:

${\ displaystyle {p_ {1}/(1-p_ {1}) \ över p_ {2}/(1-p_ {2})} = {p_ {1}/q_ {1} \ över p_ {2} /q_ {2}} = {\ frac {\; p_ {1} q_ {2} \;} {\; p_ {2} q_ {1} \;}},}$

där q _x  = 1 -  p _x . Ett oddskvot på 1 indikerar att tillståndet eller händelsen som studeras är lika sannolikt att inträffa i båda grupperna. Ett oddsförhållande som är större än 1 indikerar att tillståndet eller händelsen är mer sannolikt att inträffa i den första gruppen. Och ett oddskvot mindre än 1 indikerar att tillståndet eller händelsen är mindre sannolikt att inträffa i den första gruppen. Oddskvoten måste vara icke -negativ om den definieras. Det är odefinierat om p ₂ q _{1 är} lika med noll, dvs om p _{2 är} lika med noll eller q _{1 är} lika med noll.

Definition i termer av gemensamma och villkorliga sannolikheter

Oddskvoten kan också definieras i termer av den gemensamma sannolikhetsfördelningen för två binära slumpmässiga variabler . Den gemensamma fördelningen av binära slumpvariabler X och Y kan skrivas

${\ displaystyle {\ begin {array} {c | cc} & Y = 1 & Y = 0 \\\ hline X = 1 & p_ {11} & p_ {10} \\ X = 0 & p_ {01} & p_ {00} \ end {array} }}$

där p ₁₁ , p ₁₀ , p ₀₁ och p ₀₀ är icke-negativa "cell sannolikheter" som summerar till en. Oddsen för Y inom de två subpopulationer som definieras av X = 1 och X = 0 är definierade i termer av de betingade sannolikheterna givna X , dvs. , P ( Y | X ) :

${\ displaystyle {\ begin {array} {c | cc} & Y = 1 & Y = 0 \\\ hline X = 1 & {\ frac {p_ {11}} {p_ {11}+p_ {10}}} & {\ frac {p_ {10}} {p_ {11}+p_ {10}}} \\ X = 0 & {\ frac {p_ {01}} {p_ {01}+p_ {00}}} och {\ frac { p_ {00}} {p_ {01}+p_ {00}}} \ end {array}}}$

Således är oddskvoten

${\ displaystyle {{\ dfrac {p_ {11}/(p_ {11}+p_ {10})} {p_ {10}/(p_ {11}+p_ {10})}} {\ bigg/} { \ dfrac {p_ {01}/(p_ {01}+p_ {00})} {p_ {00}/(p_ {01}+p_ {00})}}}} {{dfrac {p_ {11} p_ {00}} {p_ {10} p_ {01}}}}$

Det enkla uttrycket till höger, ovan, är lätt att komma ihåg som en produkt av sannolikheterna för "konkordanta celler" ( X  =  Y ) dividerat med produkten av sannolikheterna för "diskordanta celler" ( X  ≠  Y ) . Observera dock att i vissa applikationer är märkningen av kategorier som noll och en godtycklig, så det är inget speciellt med överensstämmande kontra motsägelsefulla värden i dessa applikationer.

Symmetri

Om vi ​​hade beräknat oddskvoten baserat på de villkorade sannolikheterna som ges Y ,

${\ displaystyle {\ begin {array} {c | cc} & Y = 1 & Y = 0 \\\ hline X = 1 & {\ frac {p_ {11}} {p_ {11}+p_ {01}}} & {\ frac {p_ {10}} {p_ {10}+p_ {00}}} \\ X = 0 & {\ frac {p_ {01}} {p_ {11}+p_ {01}}} och {\ frac { p_ {00}} {p_ {10}+p_ {00}}} \ end {array}}}$

vi skulle ha fått samma resultat

${\ displaystyle {{\ dfrac {p_ {11}/(p_ {11}+p_ {01})} {p_ {01}/(p_ {11}+p_ {01})}} {\ bigg/} { \ dfrac {p_ {10}/(p_ {10}+p_ {00})} {p_ {00}/(p_ {10}+p_ {00})}}}} {{dfrac {p_ {11} p_ {00}} {p_ {10} p_ {01}}}.}$

Andra mått på effektstorlek för binära data, såsom den relativa risken, har inte denna symmetriegenskap.

Förhållande till statistiskt oberoende

Om X och Y är oberoende kan deras gemensamma sannolikheter uttryckas i termer av deras marginella sannolikheter p _x  =  P ( X  = 1) och p _y  =  P ( Y  = 1) enligt följande

${\ displaystyle {\ begin {array} {c | cc} & Y = 1 & Y = 0 \\\ hline X = 1 & p_ {x} p_ {y} & p_ {x} (1-p_ {y}) \\ X = 0 & (1-p_ {x}) p_ {y} & (1-p_ {x}) (1-p_ {y}) \ end {array}}}$

I det här fallet är oddskvoten lika med en, och omvänt kan oddskvoten bara motsvara en om de gemensamma sannolikheterna kan räknas in på detta sätt. Således är oddskvoten lika med en om och bara om X och Y är oberoende .

Återställa cellens sannolikheter från oddskvoten och marginella sannolikheter

Oddskvoten är en funktion av cellens sannolikheter, och omvänt kan cellsannolikheterna återvinnas med kännedom om oddskvoten och de marginella sannolikheterna P ( X  = 1) =  p ₁₁  +  p ₁₀ och P ( Y  = 1) =  s ₁₁  +  s ₀₁ . Om oddskvoten R skiljer sig från 1, då

${\ displaystyle p_ {11} = {\ frac {1+ (p_ {1 \ cdot}+p _ {\ cdot 1}) (R-1) -S} {2 (R-1)}}}}$

där p _{1 •}  =  p ₁₁  +  p ₁₀ ,   p _{• 1}  =  p ₁₁  +  p ₀₁ , och

${\ displaystyle S = {\ sqrt {(1+ (p_ {1 \ cdot}+p _ {\ cdot 1}) (R-1))^{2}+4R (1-R) ​​p_ {1 \ cdot} p _ {\ cdot 1}}}.}$

I det fall där R  = 1 har vi oberoende, så p ₁₁  =  p _{1 •} p _{• 1} .

När vi väl har p ₁₁ kan de tre andra cell sannolikheterna lätt återvinnas från de marginella sannolikheterna.

Exempel

Ett diagram som visar hur förhållandet den log odds avser de underliggande sannolikheter om resultatet X uppträder i två grupper, betecknade A och B . Den log odds ratio visas här är baserad på oddsen för den händelse som inträffar i grupp B i förhållande till oddsen för den händelse som inträffar i grupp A . Således, när sannolikheten för att X förekommer i grupp B är större än sannolikheten för att X ska uppstå i grupp A , är oddskvoten större än 1 och logoddsförhållandet är större än 0.

Antag att i ett urval på 100 män drack 90 vin under föregående vecka (så 10 gjorde inte), medan i ett urval på 80 kvinnor endast 20 drack vin under samma period (så 60 inte). Detta bildar beredskapstabellen:

${\ displaystyle {\ begin {array} {c | cc} & M = 1 & M = 0 \\\ hline D = 1 & 90 & 20 \\ D = 0 & 10 & 60 \ end {array}}}$

Oddskvoten (OR) kan beräknas direkt från denna tabell som:

${\ displaystyle {OR} = {\ frac {\; 90 \ gånger 60 \;} {\; 10 \ gånger 20 \;}} = 27}$

Alternativt är oddsen för att en man dricker vin 90 till 10 eller 9: 1, medan oddsen för en kvinna som dricker vin är bara 20 till 60, eller 1: 3 = 0,33. Oddskvoten är således 9/0,33 eller 27, vilket visar att män är mycket mer benägna att dricka vin än kvinnor. Den detaljerade beräkningen är:

${\ displaystyle {0.9/0.1 \ over 0.2/0.6} = {\ frac {\; 0.9 \ times 0.6 \;} {\; 0.1 \ times 0.2 \;}} = {0.54 \ over 0.02} = 27}$

Detta exempel visar också hur oddskvoten ibland är känsliga när de anger relativa positioner: i detta prov är män (90/100)/(20/80) = 3,6 gånger så stor risk att ha druckit vin än kvinnor, men har 27 gånger oddsen. Logaritmen för oddskvoten, skillnaden av de logits av sannolikheter , tempers denna effekt, och gör också den åtgärd symmetriska med avseende på ordningen av grupper. Till exempel, med hjälp av naturliga logaritmer , ett oddsförhållande på 27/1 kartor till 3.296 och ett oddskvot på 1/27 kartor till -3.296.

Statistisk slutsats

En graf som visar minimivärdet för statistikprovet loggoddsförhållande som måste observeras för att anses vara signifikant på 0,05 -nivån för en given provstorlek. De tre raderna motsvarar olika inställningar för marginalsannolikheterna i 2 × 2 -beredskapstabellen (rad- och kolumnmarginalsannolikheterna är lika i denna graf).

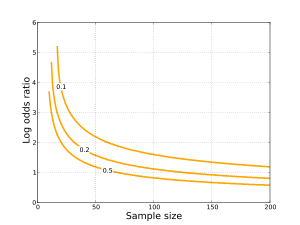
Flera tillvägagångssätt för statistisk slutsats för oddskvoter har utvecklats.

Ett tillvägagångssätt för inferens använder stora samplingsnärmningar till samplingsfördelningen av loggoddsförhållandet (den naturliga logaritmen för oddskvoten). Om vi ​​använder den gemensamma sannolikhetsnotationen som definierats ovan är populationsloggoddsförhållandet

${\ displaystyle {\ log \ left ({\ frac {p_ {11} p_ {00}} {p_ {01} p_ {10}}} \ right) = \ log (p_ {11})+\ log (p_ {00} {\ big)}-\ log (p_ {10})-\ log (p_ {01})}. \,}$

Om vi ​​observerar data i form av en beredskapstabell

${\ displaystyle {\ begin {array} {c | cc} & Y = 1 & Y = 0 \\\ hline X = 1 & n_ {11} & n_ {10} \\ X = 0 & n_ {01} & n_ {00} \ end {array} }}$

då kan sannolikheterna i den gemensamma fördelningen uppskattas till

${\ displaystyle {\ begin {array} {c | cc} & Y = 1 & Y = 0 \\\ hline X = 1 & {\ hat {p}} _ {11} & {\ hat {p}} _ {10} \ \ X = 0 & {\ hat {p}} _ {01} & {\ hat {p}} _ {00} \ end {array}}}$

var ︿sid_ij  =  n _ij  /  n , där n  =  n ₁₁  +  n ₁₀  +  n ₀₁  +  n ₀₀ är summan av alla fyra celltal. Samplingsloggoddsförhållandet är

${\ displaystyle {L = \ log \ left ({\ dfrac {{\ hat {p}} _ {11} {\ hat {p}} _ {00}} {{\ hat {p}} _ {10} {\ hat {p}} _ {01}}} \ höger) = \ log \ vänster ({\ dfrac {n_ {11} n_ {00}} {n_ {10} n_ {01}}} \ höger)} }$.

Fördelningen av loggoddsförhållandet är ungefär normal med:

${\ displaystyle L \ \ sim \ {\ mathcal {N}} (\ log (OR), \, \ sigma ^{2}). \,}$

Den standardfelet för kvoten log odds är ungefär

${\ displaystyle {{\ rm {SE}} = {\ sqrt {{\ dfrac {1} {n_ {11}}}+{\ dfrac {1} {n_ {10}}}+{\ dfrac {1} {n_ {01}}}+{\ dfrac {1} {n_ {00}}}}}}}}$.

Detta är en asymptotisk approximation och kommer inte att ge ett meningsfullt resultat om någon av celltalen är mycket små. Om L är urvalet loggoddsförhållande är ett ungefärligt 95% konfidensintervall för populationsloggoddsförhållandet L  ± 1,96SE . Detta kan mappas till exp ( L  - 1.96SE), exp ( L  + 1.96SE) för att erhålla ett 95% konfidensintervall för oddskvoten. Om vi vill testa hypotesen att förhållandet befolkningens odds är lika med ett, det tvåsidiga p-värde är 2 P ( Z  <- | L | / SE) , där P betecknar en sannolikhet, och Z betecknar en standardiserad normalfördelad slumpvariabel .

Ett alternativt tillvägagångssätt för inferens för oddskvoter utseende på fördelningen av de data som villkor på de marginella frekvenser av X och Y . En fördel med detta tillvägagångssätt är att samplingsfördelningen av oddskvoten kan uttryckas exakt.

Roll i logistisk regression

Logistisk regression är ett sätt att generalisera oddskvoten utöver två binära variabler. Antag att vi har en binär svarsvariabel Y och en binär prediktorvariabel X , och dessutom har vi andra prediktorvariabler Z ₁ , ..., Z _p som kan vara binära eller inte. Om vi ​​använder multipel logistisk regression för att regressera Y på X , Z ₁ , ..., Z _p , är den uppskattade koefficienten för X relaterad till ett villkorligt oddsförhållande. Specifikt på befolkningsnivå ${\ displaystyle {\ hat {\ beta}} _ {x}}$

${\ displaystyle e^{\ beta _ {x}} = \ exp (\ beta _ {x}) = {\ frac {P (Y = 1 \ mid X = 1, Z_ {1}, \ ldots, Z_ { p})/P (Y = 0 \ mid X = 1, Z_ {1}, \ ldots, Z_ {p})} {P (Y = 1 \ mid X = 0, Z_ {1}, \ ldots, Z_ {p})/P (Y = 0 \ mid X = 0, Z_ {1}, \ ldots, Z_ {p})}}}}$

så är en uppskattning av detta villkorade oddskvot. Tolkningen av är som en uppskattning av oddskvoten mellan Y och X när värdena för Z ₁ , ..., Z _p hålls fasta. ${\ displaystyle \ exp ({\ hat {\ beta}} _ {x})}$${\ displaystyle \ exp ({\ hat {\ beta}} _ {x})}$

Okänslighet för typen av provtagning

Om data utgör ett "populationsprov", då cellens sannolikheter ∧sid_ij tolkas som frekvenserna för var och en av de fyra grupperna i befolkningen enligt derasX-ochY-värden. I många inställningar är det opraktiskt att få ett populationsprov, så ett valt urval används. Till exempel kan vi välja att samplaenhetermed X  = 1med en given sannolikhetf, oavsett deras frekvens i populationen (vilket skulle kräva samplingsenheter med X  = 0med sannolikhet1 -  f ). I denna situation skulle våra uppgifter följa följande gemensamma sannolikheter:

${\ displaystyle {\ begin {array} {c | cc} & Y = 1 & Y = 0 \\\ hline X = 1 & {\ frac {fp_ {11}} {p_ {11}+p_ {10}}} & {\ frac {fp_ {10}} {p_ {11}+p_ {10}}} \\ X = 0 & {\ frac {(1-f) p_ {01}} {p_ {01}+p_ {00}}} & {\ frac {(1-f) p_ {00}} {p_ {01}+p_ {00}}} \ end {array}}}$

Den odds ratio p ₁₁ p ₀₀  /  p ₀₁ p ₁₀ för denna fördelning är inte beroende av värdet av f . Detta visar att oddskvoten (och följaktligen logoddsförhållandet) är oföränderlig till icke-slumpmässigt provtagning baserat på en av de variabler som studeras. Observera dock att standardfelet för loggoddsförhållandet beror på värdet av f .

Detta faktum utnyttjas i två viktiga situationer:

• Antag att det är obekvämt eller opraktiskt att få ett populationsprov, men det är praktiskt att få ett bekvämt urval av enheter med olika X -värden, så att inom X  = 0 och X  = 1 delproverna är Y -värdena representativa för befolkningen (dvs. de följer rätt villkorliga sannolikheter).
• Antag att marginalfördelningen av en variabel, säg X , är mycket sned. Till exempel, om vi studerar sambandet mellan hög alkoholkonsumtion och bukspottkörtelcancer i befolkningen i allmänhet, skulle förekomsten av bukspottkörtelcancer vara mycket låg, så det skulle kräva ett mycket stort befolkningsprov för att få ett måttligt antal fall av bukspottskörtelcancer. Men vi kan använda data från sjukhus för att kontakta de flesta eller alla deras cancer i bukspottskörteln, och sedan slumpmässigt ta ett lika stort antal patienter utan bukspottskörtelcancer (detta kallas en "fallkontrollstudie").

I båda dessa inställningar kan oddskvoten beräknas från det valda urvalet, utan att snedvrida resultaten i förhållande till vad som skulle ha erhållits för ett populationsprov.

Användning i kvantitativ forskning

På grund av den utbredda användningen av logistisk regression används oddskvoten i stor utsträckning inom många områden inom medicinsk och samhällsvetenskaplig forskning. Oddskvoten används ofta i undersökningsforskning , i epidemiologi och för att uttrycka resultaten från vissa kliniska prövningar , till exempel i fallkontrollstudier . Det förkortas ofta "ELLER" i rapporter. När data från flera undersökningar kombineras kommer det ofta att uttryckas som "poolat ELLER".

Relation till relativ risk

Riskförhållande vs Oddsförhållande

Som förklaras i avsnittet "Motiverande exempel" är den relativa risken vanligtvis bättre än oddskvoten för att förstå sambandet mellan risk och någon variabel som strålning eller ett nytt läkemedel. Det avsnittet förklarar också att om antagandet om sällsynta sjukdomar håller, är oddskvoten en bra approximation till relativ risk och att den har vissa fördelar jämfört med relativ risk. När antagandet om sällsynta sjukdomar inte håller kan oddskvoten överskatta den relativa risken.

Om den absoluta risken i den oexponerade gruppen är tillgänglig beräknas omvandlingen mellan de två med:

${\ displaystyle Relative \; Risk \ approx {\ frac {Odds \; Ratio} {1-R_ {C}+(R_ {C} \ times Odds \; Ratio)}}}}$

där R _C är den absoluta risken för den oexponerade gruppen.

Om antagandet om sällsynta sjukdomar inte gäller kan oddskvoten skilja sig mycket från den relativa risken och kan vara vilseledande.

Tänk på dödsfallet för män och kvinnor passagerare när Titanic sjönk. Av 462 kvinnor dog 154 och 308 överlevde. Av 851 män dog 709 och 142 överlevde. Det är uppenbart att en man på Titanic var mer benägna att dö än en kvinna, men hur mycket mer sannolikt? Eftersom över hälften av passagerarna dog bryts antagandet om sällsynta sjukdomar starkt.

För att beräkna oddskvoten, notera att för kvinnor var oddsen för att dö 1 till 2 (154/308). För män var oddsen 5 till 1 (709/142). Oddskvoten är 9,99 (4,99/.5). Män hade tio gånger chansen att dö som kvinnor.

För kvinnor var sannolikheten för död 33% (154/462). För män var sannolikheten 83% (709/851). Den relativa risken för dödsfall är 2,5 (.83/.33). En man hade 2,5 gånger en kvinnas sannolikhet att dö.

Vilket tal representerar korrekt hur mycket farligare det var att vara en man på Titanic? Relativ risk har fördelen av att vara lättare att förstå och att bättre representera hur människor tänker.

Förvirring och överdrift

Oddsförhållanden har ofta förväxlats med relativ risk i medicinsk litteratur. För icke-statistiker är oddskvoten ett svårt begrepp att förstå, och det ger en mer imponerande siffra för effekten. De flesta författare anser dock att den relativa risken är lätt att förstå. I en studie var medlemmar av en nationell sjukdomsstiftelse faktiskt 3,5 gånger mer sannolika än icke-medlemmar att ha hört talas om en vanlig behandling för den sjukdomen-men oddskvoten var 24 och tidningen uppgav att medlemmarna var mer än 20-faldigt mer sannolika att ha hört talas om 'behandlingen. En studie av artiklar publicerade i två tidskrifter rapporterade att 26% av artiklarna som använde ett oddskvot tolkade det som en riskkvot.

Detta kan återspegla den enkla processen med obegripliga författare som väljer den mest imponerande och publicerbara figuren. Men dess användning kan i vissa fall vara avsiktligt vilseledande. Det har föreslagits att oddskvoten bara ska presenteras som ett mått på effektstorlek när riskkvoten inte kan uppskattas direkt.

Inverterbarhet och oföränderlighet

Oddskvoten har en annan unik egenskap att vara direkt matematiskt inverterbar oavsett om man analyserar OR som antingen sjukdomsöverlevnad eller sjukdomsdebutincidens - där OR för överlevnad är direkt ömsesidigt med 1/OR för risk. Detta är känt som '' oddskvoten ''. Däremot besitter den relativa risken inte denna matematiska invertibla egenskap när man studerar sjukdomens överlevnad jämfört med debutincidensen. Detta fenomen ELLER inverterbarhet kontra RR-icke-inverterbarhet illustreras bäst med ett exempel:

Antag att i en klinisk prövning har en en biverkningsrisk på 4/100 i läkemedelsgruppen och 2/100 i placebo ... vilket ger en RR = 2 och OR = 2,04166 för läkemedels-mot-placebo-negativ risk. Men om analysen var inverterad och biverkningar istället analyserades som händelsefri överlevnad, skulle läkemedelsgruppen ha en hastighet på 96/100 och placebogruppen ha en hastighet på 98/100-vilket gav en läkemedel-mot-placebo en RR = 0,9796 för överlevnad, men en OR = 0,48979. Som man kan se är en RR på 0,9796 uppenbarligen inte ömsesidig för en RR på 2. Däremot är en OR på 0,48979 verkligen den direkta ömsesidigheten för en OR på 2,04166.

Detta är återigen det som kallas '' oddsenhetens invarians '', och varför en RR för överlevnad inte är samma sak som en RR för risk, medan OR har denna symmetriska egenskap när man analyserar antingen överlevnad eller negativ risk. Faran för klinisk tolkning för OR kommer när biverkningsfrekvensen inte är sällsynt, och därmed överdriver skillnader när antagandet om OR-sällsynta sjukdomar inte uppfylls. Å andra sidan, när sjukdomen är sällsynt, kan en RR för överlevnad (t.ex. RR = 0,9796 från exemplet ovan) kliniskt dölja och dölja en viktig fördubbling av den negativa risken i samband med ett läkemedel eller exponering.

Uppskattare av oddskvoten

Exempel på oddskvot

Den prov odds ratio n ₁₁ n ₀₀  /  n ₁₀ n ₀₁ är enkel att beräkna, och för måttliga och stora prover utför samt en bedömare av förhållandet befolkningens odds. När en eller flera av cellerna i beredskapstabellen kan ha ett litet värde kan provoddsförhållandet vara förspänt och uppvisa hög varians .

Alternativa uppskattare

Ett antal alternativa uppskattare av oddskvoten har föreslagits för att hantera begränsningar av provoddsförhållandet. En alternativ uppskattare är den villkorliga maximala sannolikhetsestimatorn, vilka förhållanden på rad- och kolumnmarginalerna när man bildar sannolikheten att maximera (som i Fishers exakta test ). En annan alternativ uppskattare är estimatorn Mantel – Haenszel .

Numeriska exempel

Följande fyra beredskapstabeller innehåller observerade celltal, tillsammans med motsvarande provoddsförhållande ( OR ) och provloggoddsförhållande ( LOR ):

Följande gemensamma sannolikhetsfördelningar innehåller populationscellssannolikheter, tillsammans med motsvarande populationsoddsförhållande ( OR ) och populationsloggoddsförhållande ( LOR ):

Numeriskt exempel

Relaterad statistik

Det finns olika andra sammanfattande statistik för beredskapstabeller som mäter samband mellan två händelser, till exempel Yules Y , Yules Q ; dessa två är normaliserade så att de är 0 för oberoende händelser, 1 för perfekt korrelerade, -1 för perfekt negativt korrelerade. Edwards (1963) studerade dessa och hävdade att dessa mått på associering måste vara funktioner i oddskvoten, som han kallade korsförhållandet .

Se även

• Cohens h
• Korsförhållande
• Diagnostiskt oddskvot
• Skogstomt
• Riskförhållande
• Sannolikhetsförhållande
• Kursförhållande

Referenser

Citat

Källor

externa länkar

• Odds Ratio Calculator - webbplats
• Odds Ratio Calculator med olika tester - webbplats
• OpenEpi, ett webbaserat program som beräknar oddskvoten, både oöverträffad och parmatchad