Kubisk ekvation - Cubic equation

I algebra är en kubisk ekvation i en variabel en ekvation av formen

${\ displaystyle ax^{3}+bx^{2}+cx+d = 0}$

där a är noll.

Lösningarna för denna ekvation kallas rötterna för den kubiska funktionen definierad av ekvatorns vänstra sida. Om alla koefficienterna a , b , c och d i kubikekvationen är reella tal , har den minst en verklig rot (detta gäller för alla udda graders polynomfunktioner ). Alla rötterna i den kubiska ekvationen kan hittas på följande sätt:

• algebraiskt , det vill säga de kan uttryckas med en kubikformel som innefattar de fyra koefficienterna, de fyra grundläggande aritmetiska operationerna och n: e rötterna (radikaler) . (Detta gäller också kvadratiska (andra graders) och kvartala (fjärde graders) ekvationer, men inte högre ekvationer, enligt Abel-Ruffini-satsen .)
• trigonometriskt
• numeriska approximationer av rötterna kan hittas med hjälp av rotfyndalgoritmer som Newtons metod .

Koefficienterna behöver inte vara riktiga tal. Mycket av det som täcks nedan gäller för koefficienter i alla fält med andra egenskaper än 2 och 3. Lösningarna i kubikekvationen tillhör inte nödvändigtvis samma fält som koefficienterna. Till exempel har vissa kubikekvationer med rationella koefficienter rötter som är irrationella (och till och med icke-verkliga) komplexa tal .

Historia

Kubikekvationer var kända för de gamla babylonierna, grekerna, kineserna, indianerna och egyptierna. Babyloniska (1900–1600 -talet f.Kr.) kilformade tabletter har hittats med tabeller för beräkning av kuber och kubrötter. Babylonierna kunde ha använt tabellerna för att lösa kubikekvationer, men det finns inga bevis för att de gjorde det. Problemet med att fördubbla kuben innebär den enklaste och äldsta studerade kubikekvationen, och en för vilken de gamla egyptierna inte trodde att det fanns någon lösning. Under 500 -talet f.Kr. reducerade Hippokrates detta problem till det att hitta två genomsnittliga proportioner mellan en linje och en annan med två gånger dess längd, men kunde inte lösa detta med en kompass- och räddningskonstruktion , en uppgift som nu är känd som omöjlig. Metoder för att lösa kubikekvationer förekommer i De nio kapitlen om matematisk konst , en kinesisk matematisk text sammanställd runt 2 -talet f.Kr. och kommenterad av Liu Hui under 300 -talet. Under 300 -talet e.Kr. fann den grekiska matematikern Diophantus heltal eller rationella lösningar för några bivariata kubikekvationer ( Diophantine ekvationer ). Hippokrates, Menaechmus och Archimedes tros ha kommit nära att lösa problemet med att fördubbla kuben med korsande koniska sektioner , även om historiker som Reviel Netz bestrider om grekerna tänkte på kubikekvationer eller bara problem som kan leda till kubikekvationer. Några andra som TL Heath , som översatte alla Archimedes verk, håller inte med och lägger fram bevis för att Archimedes verkligen löste kubiska ekvationer med hjälp av korsningar mellan två koner , men diskuterade också villkoren där rötterna är 0, 1 eller 2.

På 800 -talet etablerade Tang -dynastins astronommatematiker Wang Xiaotong i sin matematiska avhandling med titeln Jigu Suanjing systematiskt upprättat och löst numeriskt 25 kubikekvationer i form x ³ + px ² + qx = N , 23 av dem med p , q ≠ 0 , och två av dem med q = 0 .

På 1000-talet gjorde den persiska poet-matematikern Omar Khayyam (1048–1131) betydande framsteg i teorin om kubikekvationer. I ett tidigt papper upptäckte han att en kubikekvation kan ha mer än en lösning och konstaterade att den inte kan lösas med hjälp av kompass- och raklinjekonstruktioner. Han hittade också en geometrisk lösning . I sitt senare arbete, Treatise on Demonstration of Problems of Algebra , skrev han en fullständig klassificering av kubiska ekvationer med allmänna geometriska lösningar som hittades med hjälp av korsande koniska sektioner .

På 1100 -talet försökte den indiske matematikern Bhaskara II att lösa kubikekvationer utan allmän framgång. Men han gav ett exempel på en kubikekvation: x ³ + 12 x = 6 x ² + 35 . På 1100-talet skrev en annan persisk matematiker, Sharaf al-Dīn al-Tūsī (1135–1213), Al-Muʿādalāt ( avhandling om ekvationer ), som behandlade åtta typer av kubikekvationer med positiva lösningar och fem typer av kubiska ekvationer som kanske inte har positiva lösningar. Han använde vad som senare skulle bli känt som " Ruffini - Horner method" till numeriskt approximera roten av en tredjegradsekvation. Han använde också begreppen maxima och minima för kurvor för att lösa kubikekvationer som kanske inte har positiva lösningar. Han förstod vikten av diskriminanten av kubikvationen för att hitta algebraiska lösningar på vissa typer av kubiska ekvationer.

I sin bok Flos kunde Leonardo de Pisa, även känd som Fibonacci (1170–1250), närma sig den positiva lösningen på kubikekvationen x ³ + 2 x ² + 10 x = 20 . Han skrev med babyloniska siffror och gav resultatet som 1,22,7,42,33,4,40 (motsvarande 1 + 22/60 + 7/60 ²  + 42/60 ³  + 33/60 ⁴  + 4/60 ⁵  + 40/60 ⁶ ), som har ett relativt fel på cirka 10 ⁻⁹ .

I början av 1500 -talet hittade den italienska matematikern Scipione del Ferro (1465–1526) en metod för att lösa en klass kubiska ekvationer, nämligen de med formen x ³ + mx = n . Faktum är att alla kubikekvationer kan reduceras till denna form om man tillåter m och n att vara negativa, men negativa tal var inte kända för honom vid den tiden. Del Ferro höll sin prestation hemlig till strax före sin död, när han berättade om det för sin elev Antonio Fior.

1530 fick Niccolò Tartaglia (1500–1557) två problem i kubikekvationer från Zuanne da Coi och meddelade att han kunde lösa dem. Han utmanades snart av Fior, vilket ledde till en berömd tävling mellan de två. Varje tävlande var tvungen att lägga upp en viss summa pengar och föreslå ett antal problem för sin rival att lösa. Den som löste fler problem inom 30 dagar skulle få alla pengarna. Tartaglia fick frågor i formen x ³ + mx = n , för vilken han hade tagit fram en allmän metod. Fior fick frågor i formen x ³ + mx ² = n , vilket visade sig vara för svårt för honom att lösa, och Tartaglia vann tävlingen.

Senare övertalades Tartaglia av Gerolamo Cardano (1501–1576) att avslöja sin hemlighet för att lösa kubikekvationer. År 1539 gjorde Tartaglia det endast under förutsättning att Cardano aldrig skulle avslöja det och att om han skrev en bok om kubik, skulle han ge Tartaglia tid att publicera. Några år senare lärde Cardano sig om del Ferros tidigare arbete och publicerade del Ferros metod i sin bok Ars Magna år 1545, vilket innebär att Cardano gav Tartaglia sex år att publicera sina resultat (med kredit till Tartaglia för en oberoende lösning). Cardanos löfte till Tartaglia sa att han inte skulle publicera Tartaglias verk, och Cardano kände att han publicerade del Ferro's, för att komma runt löftet. Ändå ledde detta till en utmaning för Cardano från Tartaglia, vilket Cardano förnekade. Utmaningen antogs så småningom av Cardanos student Lodovico Ferrari (1522–1565). Ferrari klarade sig bättre än Tartaglia i tävlingen, och Tartaglia tappade både sin prestige och sin inkomst.

Cardano märkte att Tartaglias metod ibland krävde att han extraherade kvadratroten av ett negativt tal. Han inkluderade till och med en beräkning med dessa komplexa tal i Ars Magna , men han förstod det inte riktigt. Rafael Bombelli studerade denna fråga i detalj och betraktas därför ofta som upptäckaren av komplexa tal.

François Viète (1540–1603) härledde oberoende den trigonometriska lösningen för kubiken med tre riktiga rötter, och René Descartes (1596–1650) förlängde Viètes arbete.

Faktorisering

Om koefficienterna för en kubikekvation är rationella tal , kan man erhålla en ekvivalent ekvation med heltalskoefficienter, genom att multiplicera alla koefficienter med en gemensam multipel av deras nämnare. En sådan ekvation

${\ displaystyle ax^{3}+bx^{2}+cx+d = 0,}$

med heltalskoefficienter sägs vara reducerbar om polynomet på vänster sida är en produkt av polynom med lägre grader. Med Gauss lemma , om ekvationen är reducerbar, kan man anta att faktorerna har heltalskoefficienter.

Att hitta rötterna till en reducerbar kubikekvation är lättare än att lösa det allmänna fallet. Faktum är att om ekvationen är reducerbar måste en av faktorerna ha graden en och därmed ha formen

${\ displaystyle qx-p}$

med q och p som helhetsintrång . Det rationella rottestet gör det möjligt att hitta q och p genom att undersöka ett begränsat antal fall (eftersom q måste vara en divisor för a , och p måste vara en divisor av d ).

Således är en rot och de andra rötterna är rötterna till den andra faktorn, som kan hittas genom polynom lång delning . Denna andra faktor är ${\ displaystyle \ textstyle x_ {1} = {\ frac {p} {q}},}$

${\ displaystyle {\ frac {a} {q}} x^{2}+{\ frac {bq+ap} {q^{2}}} x+{\ frac {cq^{2}+bpq+ap^ {2}} {q^{3}}}}$

(Koefficienterna verkar inte vara heltal, men måste vara heltal om p / q är en rot.)

De andra rötterna är sedan rötterna till detta kvadratiska polynom och kan hittas med hjälp av den kvadratiska formeln .

Deprimerad kubik

Kubiker i formen

${\ displaystyle t^{3}+pt+q}$

sägs vara deprimerade. De är mycket enklare än allmänna kubik, men är grundläggande, eftersom studien av vilken kubik som helst kan reduceras med en enkel förändring av variabeln till en deprimerad kubik.

Låta

${\ displaystyle ax^{3}+bx^{2}+cx+d = 0}$

vara en kubikekvation. Ändringen av variabel

${\ displaystyle x = t-{\ frac {b} {3a}}}$

ger en kubik (i t ) som inte har någon term i t ² .

Efter att ha dividerat med en får den deprimerade kubikekvationen

${\ displaystyle t^{3}+pt+q = 0,}$

med

${\ displaystyle {\ begin {align} t = {} & x+{\ frac {b} {3a}} \\ p = {} & {\ frac {3ac-b^{2}} {3a^{2}} } \\ q = {} & {\ frac {2b^{3} -9abc+27a^{2} d} {27a^{3}}}. \ end {align}}}$

De rötter i den ursprungliga ekvationen är relaterade till rötterna av deprimerad ekvationen av relationerna ${\ displaystyle x_ {1}, x_ {2}, x_ {3}}$${\ displaystyle t_ {1}, t_ {2}, t_ {3}}$

${\ displaystyle x_ {i} = t_ {i}-{\ frac {b} {3a}},}$

för . ${\ displaystyle i = 1,2,3}$

Diskriminerande och karaktär av rötterna

Arten (verklig eller inte, distinkt eller inte) av rötterna på en kubik kan bestämmas utan att beräkna dem uttryckligen genom att använda diskriminanten .

Diskriminerande

Den diskriminant av en polynom är en funktion av dess koefficienter som är noll om och endast om polynomet har en multipel rot , eller, om det är delbart med kvadraten av en icke-konstant polynom. Med andra ord är diskriminanten icke-noll om och bara om polynomet är kvadratfritt .

Om r ₁ , r ₂ , r ₃ är de tre rötterna (inte nödvändigtvis distinkta eller verkliga ) för kubiken så är diskriminanten ${\ displaystyle ax^{3}+bx^{2}+cx+d,}$

${\ displaystyle a^{4} (r_ {1} -r_ {2})^{2} (r_ {1} -r_ {3})^{2} (r_ {2} -r_ {3})^ {2}.}$

Den deprimerade av den deprimerade kubiken är ${\ displaystyle t^{3}+pt+q}$

${\ displaystyle -\ left (4 \, p^{3} +27 \, q^{2} \ right).}$

Den allmänna kubikens diskriminant är ${\ displaystyle ax^{3}+bx^{2}+cx+d}$

${\ displaystyle 18 \, abcd-4 \, b^{3} d+b^{2} c^{2} -4 \, ac^{3} -27 \, a^{2} d^{2 }.}$

Det är produkten av och diskriminanten av motsvarande deprimerad kubik. Med hjälp av formeln för den allmänna kubiken och den associerade deprimerade kubiken innebär detta att diskriminanten för den allmänna kubiken kan skrivas som ${\ displaystyle a^{4}}$

${\ displaystyle {\ frac {4 (b^{2} -3ac)^{3}-(2b^{3} -9abc+27a^{2} d)^{2}} {27a^{2}} }.}$

Det följer att en av dessa två diskriminanter är noll om och bara om den andra också är noll, och om koefficienterna är verkliga , har de två diskriminerande samma tecken. Sammanfattningsvis kan samma information härledas från någon av dessa två diskriminanter.

För att bevisa de föregående formlerna kan man använda Vietas formler för att uttrycka allt som polynom i r ₁ , r ₂ , r ₃ och a . Beviset resulterar sedan i verifieringen av likheten mellan två polynom.

Rötternas natur

Om koefficienterna för ett polynom är reella tal , och dess diskriminant inte är noll, finns det två fall: ${\ displaystyle \ Delta}$

• Om kubiken har tre distinkta riktiga rötter${\ displaystyle \ Delta> 0,}$
• Om kubiken har en riktig rot och två icke-verkliga komplexa konjugerade rötter.${\ displaystyle \ Delta <0,}$

Detta kan bevisas enligt följande. För det första, om r är en rot till ett polynom med verkliga koefficienter, så är dess komplexa konjugat också en rot. Så de icke-riktiga rötterna, om några, förekommer som par av komplexa konjugerade rötter. Eftersom en kubisk polynom har tre rötter (inte nödvändigtvis distinkta) med grundsatsen om algebra , måste minst en rot vara verklig.

Som nämnts ovan, om r ₁ , r ₂ , r ₃ är kubikens tre rötter , så är diskriminanten ${\ displaystyle ax^{3}+bx^{2}+cx+d}$

${\ displaystyle \ Delta = a^{4} (r_ {1} -r_ {2})^{2} (r_ {1} -r_ {3})^{2} (r_ {2} -r_ {3 })^{2}}$

Om de tre rötterna är verkliga och distinkta, är den diskriminerande en produkt av positiva realer, det vill säga ${\ displaystyle \ Delta> 0.}$

Om bara en rot, säg r ₁ , är verklig, så är r ₂ och r ₃ komplexa konjugat, vilket innebär att r ₂ - r ₃ är ett rent imaginärt tal , och därmed att ( r ₂ - r ₃ ) ² är reellt och negativ. Å andra sidan är r ₁ - r ₂ och r ₁ - r ₃ komplexa konjugat, och deras produkt är verklig och positiv. Således är den diskriminerande produkten av ett enda negativt tal och flera positiva. Det är${\ displaystyle \ Delta <0.}$

Flera rot

Om diskriminanten för en kubik är noll, har kubiken en multipelrot . Om dess koefficienter dessutom är verkliga, så är alla dess rötter verkliga.

Den deprimerade av den deprimerade kubiken är noll om Om p också är noll, då är p = q = 0 , och 0 är en trippelrot av kubiken. Om och p ≠ 0 , har kubiken en enkel rot ${\ displaystyle \; t^{3}+pt+q \;}$${\ displaystyle 4p^{3}+27q^{2} = 0 \ ;.}$${\ displaystyle \; 4p^{3}+27q^{2} = 0 \ ;,}$

${\ displaystyle t_ {1} = {\ frac {\, 3q \,} {p}}}$

och en dubbelrot

${\ displaystyle t_ {2} = t_ {3} =-{\ frac {\, 3q \,} {2p}} ~.}$

Med andra ord,

${\ displaystyle t^{3}+pt+q = \ vänster (t-{\ frac {3q} {p}} \ höger) \ vänster (t+{\ frac {\, 3q \,} {2p}} \ höger)^{2} \ ;.}$

Detta resultat kan bevisas genom att expandera den senare produkten eller hämtas genom att lösa det ganska enkla ekvationssystemet som härrör från Vietas formler .

Genom att använda reduktionen av en deprimerad kubik kan dessa resultat utvidgas till den allmänna kubiken. Detta ger: Om kubikens diskriminant är noll, då ${\ displaystyle \; ax^{3}+bx^{2}+cx+d \;}$

• antingen om kubiken har en trippelrot${\ displaystyle b^{2} = 3ac \ ;,}$

${\ displaystyle x_ {1} = x_ {2} = x_ {3} =-{\ frac {b} {\, 3a \,}} ~,}$

och

${\ displaystyle ax^{3}+bx^{2}+cx+d = a \ vänster (x+{\ frac {b} {\, 3a \,}} \ höger)^{3}}$

• eller, om kubiken har en dubbelrot${\ displaystyle \; b^{2} \ neq 3ac \ ;,}$

${\ displaystyle x_ {2} = x_ {3} = {\ frac {9ad-bc} {\, 2 (b^{2} -3ac) \,}} ~,}$

och en enkel rot,

${\ displaystyle x_ {1} = {\ frac {\, 4abc-9a^{2} db^{3} \,} {a (b^{2} -3ac)}} ~.}$

och sålunda

${\ displaystyle ax^{3}+bx^{2}+cx+d = a \, \ left (x-x_ {1} \ right) \ left (x-x_ {2} \ right)^{2} ~.}$

Karakteristik 2 och 3

Ovanstående resultat är giltiga när koefficienterna tillhör ett fält av karakteristiska annat än två eller tre, men måste modifieras för karakteristisk 2 eller 3, på grund av de involverade divisioner med två och tre.

Reduktionen till en deprimerad kubik fungerar för karakteristik 2, men inte för karakteristik 3. Men i båda fallen är det enklare att fastställa och ange resultaten för den allmänna kubiken. Huvudverktyget för det är det faktum att en multipelrot är en gemensam rot till polynomet och dess formella derivat . I dessa egenskaper, om derivatet inte är en konstant, har det en enda rot, som är linjär i karakteristiken 3, eller kvadraten för ett linjärt polynom i karakteristiken 2. Detta gör det möjligt att beräkna multipelrot, och den tredje roten kan härledas från summan av rötterna, som tillhandahålls av Vietas formler .

En skillnad med andra egenskaper är att i karakteristik 2 innebär formeln för en dubbelrot en kvadratrot, och i karakteristiken 3 innebär formeln för en trippelrot en kubrot.

Cardanos formel

Gerolamo Cardano krediteras för att ha publicerat den första formeln för att lösa kubikekvationer, tillskriva den till Scipione del Ferro . Formeln gäller deprimerade kubik, men som visas i § Deprimerad kubik gör det möjligt att lösa alla kubiska ekvationer.

Cardanos resultat är att, if

${\ displaystyle t^{3}+pt+q = 0}$

är en kubisk ekvation så att p och q är reella tal så att ekvationen har den verkliga roten ${\ displaystyle 4p^{3}+27q^{2}> 0,}$

${\ displaystyle {\ sqrt [{3}] {-{\ frac {q} {2}}+{\ sqrt {{\ frac {q^{2}} {4}}+{\ frac {p^{ 3}} {27}}}}}}+{\ sqrt [{3}] {-{\ frac {q} {2}}-{\ sqrt {{\ frac {q^{2}} {4} }+{\ frac {p^{3}} {27}}}}}}}$

Se § Härledning av rötterna nedan för flera metoder för att få detta resultat.

Som visas i § Rötternas natur är de två andra rötterna icke-verkliga komplexa konjugerade tal, i detta fall. Det visades senare (Cardano visste inte komplexa tal ) att de två andra rötterna erhålls genom att multiplicera någon av kubrötterna med den primitiva kubroten av enhet och den andra kubroten med${\ displaystyle {\ frac {-1+i {\ sqrt {3}}} {2}},}$${\ displaystyle {\ frac {-1-i {\ sqrt {3}}} {2}}.}$

Om det finns tre verkliga rötter, men Galois -teorin gör det möjligt att bevisa att om det inte finns någon rationell rot kan rötterna inte uttryckas med ett algebraiskt uttryck som endast innefattar reella tal. Därför kan ekvationen inte lösas i detta fall med kunskap om Cardanos tid. Detta fall har alltså kallats casus irreducibilis , vilket betyder irreducerbart fall på latin. ${\ displaystyle 4p^{3}+27q^{2} <0,}$

I casus irreducibilis kan Cardanos formel fortfarande användas, men viss försiktighet krävs vid användning av kubrötter. En första metod är att definiera symbolerna och representera rotfunktionens huvudvärden (det är roten som har den största verkliga delen). Med denna konvention förblir Cardanos formel för de tre rötterna giltig, men är inte rent algebraisk, eftersom definitionen av en huvuddel inte är rent algebraisk, eftersom den innebär ojämlikheter för att jämföra verkliga delar. Användningen av huvudkubrot kan också ge ett felaktigt resultat om koefficienterna är icke-reella komplexa tal. Dessutom, om koefficienterna tillhör ett annat fält , definieras inte huvudkubrotet i allmänhet. ${\ displaystyle {\ sqrt {{~}^{~}}}}$${\ displaystyle {\ sqrt [{3}] {{~}^{~}}}}$

Det andra sättet att göra Cardanos formel alltid korrekt är att anmärka att produkten från de två kubrötterna måste vara - p / 3 . Det resulterar i att en rot i ekvationen är

${\ displaystyle C-{\ frac {p} {3C}} \ quad {\ text {med}} \ quad C = {\ sqrt [{3}] {-{\ frac {q} {2}}+{ \ sqrt {{\ frac {q^{2}} {4}}+{\ frac {p^{3}} {27}}}}}}}$

I denna formel, symbolerna och beteckna eventuell kvadratrot och vilken kubrot som helst. Ekvationens andra rötter erhålls antingen genom att byta kubrot eller, på motsvarande sätt, genom att multiplicera kubroten med en primitiv kubrot av enhet, det vill säga${\ displaystyle {\ sqrt {{~}^{~}}}}$${\ displaystyle {\ sqrt [{3}] {{~}^{~}}}}$${\ displaystyle \ textstyle {\ frac {-1 \ pm {\ sqrt {-3}}} {2}}.}$

Denna formel för rötterna är alltid korrekt utom när p = q = 0 , med förbehållet att om p = 0 , är kvadratroten vald så att C ≠ 0 . Formeln är dock värdelös i dessa fall eftersom rötterna kan uttryckas utan någon kubrot. På samma sätt är formeln också värdelös i de andra fallen där ingen kubrot behövs, det vill säga när och när det kubiska polynomet inte är oreducerbart . ${\ displaystyle 4p^{3}+27q^{2} = 0}$

Denna formel är också korrekt när p och q tillhör något fält av karakteristiska annat än två eller tre.

Allmän kubikformel

En kubikformel för rötterna i den allmänna kubikekvationen (med en ≠ 0 )

${\ displaystyle ax^{3}+bx^{2}+cx+d = 0}$

kan härledas från varje variant av Cardanos formel genom reduktion till en deprimerad kubik . Varianten som presenteras här gäller inte bara för verkliga koefficienter, utan också för koefficienterna a , b , c , d som tillhör alla områden av karakteristika som skiljer sig från 2 och 3.

Formeln är ganska komplicerad, det är värt att dela den i mindre formler.

Låta

${\ displaystyle {\ begin {align} \ Delta _ {0} & = b^{2} -3ac, \\\ Delta _ {1} & = 2b^{3} -9abc+27a^{2} d. \ end {align}}}$

(Både och kan uttryckas som resultat av kubiken och dess derivat: är${\ displaystyle \ Delta _ {0}}$${\ displaystyle \ Delta _ {1}}$${\ displaystyle \ Delta _ {1}}$−1/8agånger resultatet av kubiken och dess andra derivat, och är${\ displaystyle \ Delta _ {0}}$−1/12a gånger resultatet av det första och andra derivatet av det kubiska polynomet.)

Sedan

${\ displaystyle C = {\ sqrt [{3}] {\ frac {\ Delta _ {1} \ pm {\ sqrt {\ Delta _ {1}^{2} -4 \ Delta _ {0}^{3 }}}} {2}}},}$

där symbolerna och tolkas som någon kvadratroten och varje kubikroten, respektive. Tecknet " ± " före kvadratroten är antingen " + " eller " - "; valet är nästan godtyckligt, och att ändra det innebär att välja en annan kvadratrot. Men om ett val ger C = 0 , det vill säga om det andra tecknet måste väljas istället. Om båda alternativen ger C = 0 , det vill säga om en bråkdel${\ displaystyle {\ sqrt {{~}^{~}}}}$${\ displaystyle {\ sqrt [{3}] {{~}^{~}}}}$${\ displaystyle \ Delta _ {0} = 0,}$${\ displaystyle \ Delta _ {0} = \ Delta _ {1} = 0,}$0/0förekommer i följande formler, som måste tolkas som lika med noll (se slutet av detta avsnitt). Sedan är en av rötterna

${\ displaystyle x =-{\ frac {1} {3a}} \ vänster (b+C+{\ frac {\ Delta _ {0}} {C}} \ höger) {\ text {.}}}$

De andra två rötterna kan erhållas genom att ändra valet av kubrot i definitionen av C , eller, ekvivalent med att multiplicera C med en primitiv kubrot av enhet , det vill säga–1 ± √ –3/2. Med andra ord är de tre rötterna

${\ displaystyle x_ {k} =-{\ frac {1} {3a}} \ vänster (b+\ xi ^{k} C+{\ frac {\ Delta _ {0}} {\ xi ^{k} C} } \ höger), \ qquad k \ in \ {0,1,2 \} {\ text {,}}}$

där ξ =–1 + √ –3/2.

När det gäller specialfallet med en deprimerad kubik, gäller denna formel men är värdelös när rötterna kan uttryckas utan kubrötter. I synnerhet om formeln ger att de tre rötterna är lika vilket innebär att det kubiska polynomet kan räknas som En enkel beräkning gör det möjligt att verifiera att förekomsten av denna faktorisering är ekvivalent med${\ displaystyle \ Delta _ {0} = \ Delta _ {1} = 0,}$${\ displaystyle {\ frac {-b} {3a}},}$${\ displaystyle \ textstyle a (x+{\ frac {b} {3a}})^{3}.}$${\ displaystyle \ Delta _ {0} = \ Delta _ {1} = 0.}$

Trigonometriska och hyperboliska lösningar

Trigonometrisk lösning för tre riktiga rötter

När en kubikekvation med verkliga koefficienter har tre verkliga rötter, involverar formlerna som uttrycker dessa rötter i termer av radikaler komplexa tal. Galois teori gör det möjligt att bevisa att när de tre rötterna är verkliga, och ingen är rationell ( casus irreducibilis ), kan man inte uttrycka rötterna i termer av verkliga radikaler. Ändå kan rent verkliga uttryck för lösningarna erhållas med hjälp av trigonometriska funktioner , specifikt när det gäller cosinus och arccosines . Mer exakt, rötterna till den deprimerade kubiken

${\ displaystyle t^{3}+pt+q = 0}$

är

${\ displaystyle t_ {k} = 2 \, {\ sqrt {-{\ frac {p} {3}}}} \, \ cos \ left [\, {\ frac {1} {3}} \ arccos \ vänster ({\ frac {3q} {2p}} {\ sqrt {\ frac {-3} {p}}} \, \ höger)-{\ frac {2 \ pi k} {3}} \, \ höger ] \ qquad {\ text {för}} k = 0,1,2.}$

Denna formel beror på François Viète . Det är rent verkligt när ekvationen har tre verkliga rötter (det vill säga ). Annars är det fortfarande korrekt men involverar komplexa cosinus och arccosines när det bara finns en verklig rot, och det är meningslöst (division med noll) när p = 0 . ${\ displaystyle 4p^{3}+27q^{2} <0}$

Denna formel kan enkelt omvandlas till en formel för rötterna i en allmän kubikekvation, med hjälp av den bakre substitution som beskrivs i § Deprimerad kubik . Det kan bevisas enligt följande:

Utifrån ekvationen t ³ + pt + q = 0 , låt oss ställa in t = u cos  θ . Tanken är att välja u för att få ekvationen att sammanfalla med identiteten  

${\ displaystyle 4 \ cos ^{3} \ theta -3 \ cos \ theta -\ cos (3 \ theta) = 0.}$

För detta, välj och dela ekvationen med Detta ger ${\ displaystyle u = 2 \, {\ sqrt {-{\ frac {p} {3}}}} \ ,,}$${\ displaystyle {\ frac {u^{3}} {4}}.}$

${\ displaystyle 4 \ cos ^{3} \ theta -3 \ cos \ theta -{\ frac {3q} {2p}} \, {\ sqrt {\ frac {-3} {p}}} = 0.}$

I kombination med ovanstående identitet får man

${\ displaystyle \ cos (3 \ theta) = {\ frac {3q} {2p}} {\ sqrt {\ frac {-3} {p}}} \ ,,}$

och rötterna är alltså

${\ displaystyle t_ {k} = 2 \, {\ sqrt {-{\ frac {p} {3}}}} \, \ cos \ left [{\ frac {1} {3}} \ arccos \ left ( {\ frac {3q} {2p}} {\ sqrt {\ frac {-3} {p}}} \ höger)-{\ frac {2 \ pi k} {3}} \ höger] \ qquad {\ text {för}} k = 0,1,2.}$

Hyperbolisk lösning för en riktig rot

När det bara finns en riktig rot (och p ≠ 0 ) kan denna rot representeras på samma sätt med hjälp av hyperboliska funktioner , som

${\ displaystyle {\ begin {align} t_ {0} & =-2 {\ frac {| q |} {q}} {\ sqrt {-{\ frac {p} {3}}}} \ cosh \ left [{\ frac {1} {3}} \ operatorname {arcosh} \ vänster ({\ frac {-3 | q |} {2p}} {\ sqrt {\ frac {-3} {p}}} \ höger ) \ höger] \ qquad {\ text {if}} ~ 4p^{3}+27q^{2}> 0 ~ {\ text {och}} ~ p <0, \\ t_ {0} & =-2 {\ sqrt {\ frac {p} {3}}} \ sinh \ left [{\ frac {1} {3}} \ operatorname {arsinh} \ left ({\ frac {3q} {2p}} {\ sqrt {\ frac {3} {p}}} \ right) \ right] \ qquad {\ text {if}} ~ p> 0. \ end {align}}}$

Om p ≠ 0 och ojämlikheterna till höger inte uppfylls (fallet med tre riktiga rötter) förblir formlerna giltiga men involverar komplexa kvantiteter.

När p = ± 3 kallas ibland ovanstående värden för t ₀ Chebyshev -kubroten. Närmare bestämt definierar värdena som involverar cosinus och hyperboliska cosinus, när p = -3 , samma analytiska funktion betecknad C _1/3 ( q ) , som är den korrekta Chebyshev -kubroten. Värdet som involverar hyperboliska siner betecknas på samma sätt S _1/3 ( q ) , när p = 3 .

Geometriska lösningar

Omar Khayyáms lösning

För att lösa den kubiska ekvationen x ³ + m ² x = n där n > 0 , Omar Khayyám konstruerat parabeln y = x ² / m , den cirkel som har som en diameter på linjesegmentet [0, n / m ² ] på positivt x -axel och en vertikal linje genom punkten där cirkeln och parabolen skär varandra ovanför x -axeln. Lösningen ges av längden på det horisontella linjesegmentet från ursprunget till skärningspunkten mellan den vertikala linjen och x -axeln (se figuren).

Ett enkelt modernt bevis är följande. Multiplicering av ekvationen med x / m ² och omgruppering av termerna ger

${\ displaystyle {\ frac {x^{4}} {m^{2}}} = x \ vänster ({\ frac {n} {m^{2}}}-x \ höger).}$

Den vänstra sidan är värdet av y ² på parabolen. Ekvationen för cirkeln är y ² + x ( x -n/m ²) = 0 , höger sida är värdet av y ² på cirkeln.

Lösning med vinkeltrisektor

En kubikekvation med verkliga koefficienter kan lösas geometriskt med hjälp av kompass, raksträcka och en vinkeltrisektor om och bara om den har tre riktiga rötter.

En kubisk ekvation kan lösas genom kompass-och-räta konstruktion (utan trisektor) om och bara om den har en rationell rot. Detta innebär att de gamla problemen med vinkeltrisektion och fördubbling av kuben , fastställda av antika grekiska matematiker , inte kan lösas genom kompass-och-räta konstruktion.

Geometrisk tolkning av rötterna

Tre riktiga rötter

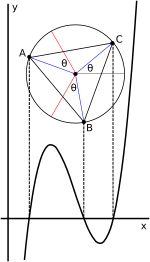
Viètes trigonometriska uttryck för rötterna i fallet med tre verkliga rötter lämpar sig för en geometrisk tolkning i form av en cirkel. När kubiken skrivs i nedtryckt form ( 2 ) , t ³ + pt + q = 0 , som visas ovan, kan lösningen uttryckas som

${\ displaystyle t_ {k} = 2 {\ sqrt {-{\ frac {p} {3}}}} \ cos \ left ({\ frac {1} {3}} \ arccos \ left ({\ frac { 3q} {2p}} {\ sqrt {\ frac {-3} {p}}} \ höger) -k {\ frac {2 \ pi} {3}} \ höger) \ quad {\ text {för}} \ quad k = 0,1,2 \ ,.}$

Här är en vinkel i enhetscirkeln; tar${\ displaystyle \ arccos \ vänster ({\ frac {3q} {2p}} {\ sqrt {\ frac {-3} {p}}} \ höger)}$1/3av den vinkeln motsvarar att ta en kubrot av ett komplext tal; lägga till - k2 π/3för k = 1, 2 hittar de andra kubrötterna; och multiplicera cosinus för dessa resulterande vinklar med korrigeringar för skalan. ${\ displaystyle 2 {\ sqrt {-{\ frac {p} {3}}}}}$

För de icke-deprimerade fallet ( 1 ) (visas i bifogad grafen), den nedtryckta fallet såsom tidigare angivits erhålles genom att definiera t sådant att x = t -b/3 aså t = x +b/3 a. Grafiskt motsvarar detta att helt enkelt flytta grafen horisontellt vid växling mellan variablerna t och x , utan att ändra vinkelförhållandena. Detta skift flyttar böjningspunkten och cirkelns mitt till y -axeln. Följaktligen är ekvationens rötter i t summa till noll.

En riktig rot

I det kartesiska planet

När grafen för en kubisk funktion är ritad i det kartesiska planet , om det bara finns en riktig rot, är det abscissen ( x -koordinat) för kurvens horisontella skärningspunkt (punkt R på figuren). Om de komplexa konjugerade rötterna dessutom skrivs som g ± hi , är den verkliga delen g abscissen för tangenspunkten H på tangentlinjen till kubik som passerar genom x -avsnitt R för kubiken (det är den signerade längden RM , negativt på figuren). De imaginära delarna ± h är kvadratrötterna hos tangenten i vinkeln mellan denna tangentlinje och den horisontella axeln.

I det komplexa planet

Med en verklig och två komplexa rötter kan de tre rötterna representeras som punkter i det komplexa planet, liksom de två rötterna i kubikens derivat. Det finns en intressant geometrisk relation mellan alla dessa rötter.

Punkterna i det komplexa planet som representerar de tre rötterna fungerar som hörn i en likbent triangel. (Triangeln är jämlik eftersom en rot är på den horisontella (verkliga) axeln och de andra två rötterna, som är komplexa konjugat, visas symmetriskt ovanför och under den verkliga axeln.) Mardens sats säger att punkterna som representerar rötterna till derivatet av kubik är fokus för triangelns Steiner -inellipse - den unika ellipsen som tangerar triangeln vid mitten av dess sidor. Om vinkeln vid hörnet på den verkliga axeln är mindre änπ/3då ligger ellipsens huvudaxel på den verkliga axeln, liksom dess foci och därmed rötterna till derivatet. Om den vinkeln är större änπ/3, huvudaxeln är vertikal och dess fokus, derivatets rötter, är komplexa konjugat. Och om den vinkeln ärπ/3, triangeln är liksidig, Steiner -inellipsen är helt enkelt triangelns cirkel, dess foci sammanfaller med varandra vid incenteret, som ligger på den verkliga axeln, och därmed har derivatet dubbletter av verkliga rötter.

Galois -gruppen

Med tanke på en kubisk oreducerbar polynom över ett fält k med karakteristik som skiljer sig från 2 och 3, är Galois -gruppen över k gruppen av fältautomorfismer som fixar k av den minsta förlängningen av k ( delningsfält ). Eftersom dessa automorfismer måste permutera rötterna av polynom, är denna grupp antingen gruppen S ₃ av alla sex permutationer av de tre rötter, eller gruppen A ₃ av de tre cirkulära permutationer.

Den diskriminerande Δ i kubiken är kvadraten av

${\ displaystyle {\ sqrt {\ Delta}} = a^{2} (r_ {1} -r_ {2}) (r_ {1} -r_ {3}) (r_ {2} -r_ {3}) ,}$

där a är den ledande koefficienten för kubiken, och r ₁ , r ₂ och r ₃ är kubikens tre rötter. Såsom förändringar av tecken om två rötter utbyts, fixeras av Galois gruppen endast om Galois gruppen är A ₃ . Med andra ord är Galois -gruppen A ₃ om och endast om diskriminanten är kvadraten för ett element av k . ${\ displaystyle {\ sqrt {\ Delta}}}$${\ displaystyle {\ sqrt {\ Delta}}}$

Eftersom de flesta heltal inte är kvadrater, när man arbetar över fältet Q för de rationella talen , är Galois -gruppen med de flesta oreducerbara kubiska polynomen gruppen S ₃ med sex element. Ett exempel på en Galois -grupp A ₃ med tre element ges av p ( x ) = x ³ - 3 x - 1 , vars diskriminant är 81 = 9 ² .

Avledning av rötterna

Detta avsnitt omgrupperar flera metoder för att härleda Cardanos formel .

Cardanos metod

Denna metod beror på Scipione del Ferro och Tartaglia , men är uppkallad efter Gerolamo Cardano som först publicerade den i sin bok Ars Magna (1545).

Denna metod gäller för en deprimerad kubisk t ³ + pt + q = 0 . Tanken är att införa två variabler u och v så att u + v = t och att ersätta detta med den deprimerade kubiken, vilket ger

${\ displaystyle u^{3}+v^{3}+(3uv+p) (u+v)+q = 0.}$

Vid denna tidpunkt ställde Cardano villkoret 3 uv + p = 0 . Detta tar bort den tredje termen i tidigare jämlikhet, vilket leder till ekvationssystemet

${\ displaystyle {\ begin {align} u^{3}+v^{3} & =-q \\ uv & =-{\ frac {p} {3}}. \ end {align}}}$

Genom att veta summan och produkten av u ³ och v ³ , kan man dra slutsatsen att de är de två lösningarna för den kvadratiska ekvationen

${\ displaystyle (xu^{3}) (xv^{3}) = x^{2}-(u^{3}+v^{3}) x+u^{3} v^{3} = x^{2}-(u^{3}+v^{3}) x+(uv)^{3} = 0,}$

så

${\ displaystyle x^{2}+qx-{\ frac {p^{3}} {27}} = 0,}$

Diskrimineraren i denna ekvation är , och förutsatt att den är positiv, verkliga lösningar på dessa ekvationer (efter vikning med 4 under kvadratroten): ${\ displaystyle \ Delta = q^{2}+{\ frac {4p^{3}} {27}}}$

${\ displaystyle -{\ frac {q} {2}} \ pm {\ sqrt {{\ frac {q^{2}} {4}}+{\ frac {p^{3}} {27}}} }.}$

Så (utan förlust av allmänhet när du väljer u eller v):

${\ displaystyle u = {\ sqrt [{3}] {-{\ frac {q} {2}}+{\ sqrt {{\ frac {q^{2}} {4}}+{\ frac {p ^{3}} {27}}}}}}.}$

${\ displaystyle v = {\ sqrt [{3}] {-{\ frac {q} {2}}-{\ sqrt {{\ frac {q^{2}} {4}}+{\ frac {p ^{3}} {27}}}}}}.}$

Som u + v = t är summan av kubrötterna i dessa lösningar en rot i ekvationen. Det är

${\ displaystyle t = {\ sqrt [{3}] {-{q \ over 2}+{\ sqrt {{q^{2} \ over 4}+{p^{3} \ over 27}}}} }+{\ sqrt [{3}] {-{q \ over 2}-{\ sqrt {{q^{2} \ over 4}+{p^{3} \ over 27}}}}}}}}$

är en rot till ekvationen; detta är Cardanos formel.

Detta fungerar bra när men, om kvadratroten som visas i formeln inte är verklig. Eftersom ett komplext tal har tre kubrötter, skulle Cardanos formel utan omsorg ge nio rötter, medan en kubikekvation inte kan ha mer än tre rötter. Detta klargjordes först av Rafael Bombelli i hans bok L'Algebra (1572). Lösningen är att använda det faktum att uv =${\ displaystyle 4p^{3}+27q^{2}> 0,}$${\ displaystyle 4p^{3}+27q^{2} <0,}$- sid/3, det är v =- sid/3 u. Detta innebär att endast en kubrot behöver beräknas och leder till den andra formeln som ges i § Cardanos formel .

Ekvationens andra rötter kan erhållas genom byte av kubrot, eller, på motsvarande sätt, genom att multiplicera kubroten med var och en av de två primitiva kubrötterna av enhet , som är${\ displaystyle {\ frac {-1 \ pm {\ sqrt {-3}}} {2}}.}$

Vietas byte

Vietas substitution är en metod som introducerades av François Viète (Vieta är hans latinska namn) i en text publicerad postumt 1615, som direkt tillhandahåller den andra formeln för § Cardanos metod , och undviker problemet med att beräkna två olika kubrötter.

Utgående från den nedtryckta kubiken t ³ + pt + q = 0 är Vietas substitution t = w -sid/3 w.

Substitutionen t = w -sid/3 w förvandlar den deprimerade kubiken till

${\ displaystyle w^{3}+q-{\ frac {p^{3}} {27w^{3}}} = 0.}$

Multiplicera med w ³ , en får en kvadratisk ekvation i w ³ :

${\ displaystyle (w^{3})^{2}+q (w^{3})-{\ frac {p^{3}} {27}} = 0.}$

Låta

${\ displaystyle W =-{\ frac {q} {2}} \ pm {\ sqrt {{\ frac {p^{3}} {27}}+{\ frac {q^{2}} {4} }}}}$

vara någon rotfri rot till denna kvadratiska ekvation. Om w ₁ , w ₂ och w ₃ är de tre kubrötterna till W , då är rötterna i den ursprungliga deprimerade kubiken w ₁ -sid/3 w ₁, w ₂ -sid/3 w ₂och w ₃ -sid/3 w ₃. Den andra roten i den kvadratiska ekvationen är Detta innebär att ändring av tecknet på kvadratrotsutbyten w _i och -${\ displaystyle \ textstyle -{\ frac {p^{3}} {27W}}.}$sid/3 w _iför i = 1, 2, 3 , och ändrar därför inte rötterna. Denna metod misslyckas bara när båda rötterna i den kvadratiska ekvationen är noll, det vill säga när p = q = 0 , i vilket fall är den enda roten till den deprimerade kubiken 0 .

Lagranges metod

I sitt papper Réflexions sur la résolution algébrique des équations ("Tankar om algebraisk lösning av ekvationer") introducerade Joseph Louis Lagrange en ny metod för att lösa ekvationer av låg grad på ett enhetligt sätt, i hopp om att han kunde generalisera det för högre grader. Denna metod fungerar bra för kubik- och kvartsekvationer , men Lagrange lyckades inte tillämpa den på en kvintisk ekvation , eftersom den kräver att man löser ett upplösande polynom med minst sex. Förutom att ingen tidigare lyckades lösa problemet, var detta den första indikationen på att det inte fanns någon algebraisk formel för grader 5 och högre; detta bevisades senare som Abel -Ruffini -satsen . Ändå är de moderna metoderna för att lösa lösbara kvintiska ekvationer huvudsakligen baserade på Lagranges metod.

När det gäller kubiska ekvationer ger Lagranges metod samma lösning som Cardanos. Lagranges metod kan tillämpas direkt på den allmänna kubiska ekvationen ax ³ + bx ² + cx + d = 0 , men beräkningen är enklare med den nedtryckta kubikekvationen, t ³ + pt + q = 0 .

Lagranges främsta idé var att arbeta med den diskreta Fouriertransformen av rötterna istället för med rötterna själva. Mer exakt, låt ξ vara en primitiv tredje rot av enhet , det vill säga ett tal så att ξ ³ = 1 och ξ ² + ξ + 1 = 0 (när man arbetar i komplexa tal , har man men denna komplexa tolkning är inte används här). Betecknar x ₀ , x ₁ och x ₂ de tre rötterna i kubikekvationen som ska lösas, låt ${\ displaystyle \ textstyle \ xi = {\ frac {-1 \ pm i {\ sqrt {3}}} {2}} = e^{2i \ pi /3},}$

${\ displaystyle {\ begin {align} s_ {0} & = x_ {0}+x_ {1}+x_ {2}, \\ s_ {1} & = x_ {0}+\ xi x_ {1}+ \ xi ^{2} x_ {2}, \\ s_ {2} & = x_ {0}+\ xi ^{2} x_ {1}+\ xi x_ {2}, \ end {align}}}$

vara den diskreta Fouriertransformen av rötterna. Om s ₀ , s ₁ och s ₂ är kända kan rötterna återvinnas från dem med den inversa Fourier -transformen som består av att invertera denna linjära transformation; det är,

${\ displaystyle {\ begin {align} x_ {0} & = {\ tfrac {1} {3}} (s_ {0}+s_ {1}+s_ {2}), \\ x_ {1} & = {\ tfrac {1} {3}} (s_ {0}+\ xi ^{2} s_ {1}+\ xi s_ {2}), \\ x_ {2} & = {\ tfrac {1} { 3}} (s_ {0}+\ xi s_ {1}+\ xi ^{2} s_ {2}). \ End {align}}}$

Enligt Vietas formler är s ₀ känt för att vara noll i fallet med en deprimerad kubik, och -b/aför den allmänna kubiken. Så bara s ₁ och s ₂ behöver beräknas. De är inte symmetriska funktioner hos rötterna (utbyte x ₁ och x ₂ utbyten också s ₁ och s ₂ ), men några enkla symmetriska funktioner för s ₁ och s ₂ är också symmetriska i rötterna i kubikekvationen som ska lösas. Sålunda kan uttryckas dessa symmetriska funktioner i termer av de (kända) koefficienterna för den ursprungliga kubiska, och detta gör det möjligt att så småningom uttrycker s _jag som rötterna av ett polynom med kända koefficienter. Detta fungerar bra för varje grad, men i grader högre än fyra, den resulterande polynom som har är _jag som rötter har en grad högre än den initiala polynomet och är därför föga för att lösa. Detta är anledningen till att Lagranges metod misslyckas i grader fem och högre.

När det gäller en kubisk ekvation, och är sådana symmetriska polynom (se nedan). Det följer att och är de två rötterna i den kvadratiska ekvationen Således kan upplösningen av ekvationen slutföras exakt som med Cardanos metod, med och i stället för u och v . ${\ displaystyle P = s_ {1} s_ {2},}$${\ displaystyle S = s_ {1}^{3}+s_ {2}^{3}}$${\ displaystyle s_ {1}^{3}}$${\ displaystyle s_ {2}^{3}}$${\ displaystyle z^{2} -Sz+P^{3} = 0.}$${\ displaystyle s_ {1}}$${\ displaystyle s_ {2}}$

När det gäller den deprimerade kubiken har man och medan vi i Cardanos metod har satt och sålunda, fram till utbytet av u och v , har vi och Med andra ord, i detta fall beräknar Cardanos metod och Lagranges metod exakt samma saker, upp till en faktor tre i hjälpvariablerna, den största skillnaden är att Lagranges metod förklarar varför dessa hjälpvariabler förekommer i problemet. ${\ displaystyle x_ {0} = {\ tfrac {1} {3}} (s_ {1}+s_ {2})}$${\ displaystyle s_ {1} s_ {2} =-3p,}$${\ displaystyle x_ {0} = u+v}$${\ displaystyle uv = {\ tfrac {1} {3}} s.}$${\ displaystyle s_ {1} = 3u}$${\ displaystyle s_ {2} = 3v.}$

Beräkning av S och P

En enkel beräkning med relationerna ξ ³ = 1 och ξ ² + ξ + 1 = 0 ger

${\ displaystyle {\ begin {align} P & = s_ {1} s_ {2} = x_ {0}^{2}+x_ {1}^{2}+x_ {2}^{2}-(x_ { 0} x_ {1}+x_ {1} x_ {2}+x_ {2} x_ {0}), \\ S & = s_ {1}^{3}+s_ {2}^{3} = 2 ( x_ {0}^{3}+x_ {1}^{3}+x_ {2}^{3})-3 (x_ {0}^{2} x_ {1}+x_ {1}^{2 } x_ {2}+x_ {2}^{2} x_ {0}+x_ {0} x_ {1}^{2}+x_ {1} x_ {2}^{2}+x_ {2} x_ {0}^{2})+12x_ {0} x_ {1} x_ {2}. \ End {align}}}$

Detta visar att P och S är symmetriska funktioner hos rötterna. Med hjälp av Newtons identiteter är det enkelt att uttrycka dem i termer av de elementära symmetriska funktionerna hos rötterna, vilket ger

${\ displaystyle {\ begin {align} P & = e_ {1}^{2} -3e_ {2}, \\ S & = 2e_ {1}^{3} -9e_ {1} e_ {2}+27e_ {3 }, \ end {align}}}$

med e ₁ = 0 , e ₂ = p och e ₃ = - q vid en deprimerad kubik och e ₁ = -b/a, e ₂ =c/aoch e ₃ = -d/a, i det allmänna fallet.

Ansökningar

Kubikekvationer uppstår i olika andra sammanhang.

I matematik

• Vinkeltrisektion och fördubbling av kuben är två gamla problem med geometri som har visat sig inte kunna lösas genom rakning och kompasskonstruktion , eftersom de motsvarar att lösa en kubikekvation.
• Mardens sats säger att fokusen för Steiner -inellipsen i vilken triangel som helst kan hittas med hjälp av den kubiska funktionen vars rötter är koordinaterna i det komplexa planet för triangelns tre hörn. Rötterna till det första derivatet av denna kubik är de komplexa koordinaterna för dessa foci.
• I området för en vanlig heptagon kan uttryckas i termer av rötterna i en kubisk. Vidare uppfyller förhållandena mellan den långa diagonalen till sidan, sidan till den korta diagonalen och den negativa av den korta diagonalen till den långa diagonalen alla en särskild kubikekvation. Dessutom är förhållandet mellan inradius och omkretsen för en heptagonal triangel en av lösningarna för en kubikekvation. Värdena för trigonometriska funktioner i vinklar relaterade till att tillfredsställa kubikekvationer.${\ displaystyle 2 \ pi /7}$
• Med tanke på cosinus (eller annan trigonometrisk funktion) för en godtycklig vinkel är cosinus för en tredjedel av den vinkeln en av rötterna i en kubik.
• Lösningen av den allmänna kvartsekvationen är beroende av lösningen av dess lösningsmedels -kubik .
• De egenvärden av en 3 x 3 matris är rötterna till en kubisk polynom som är det karakteristiska polynomet av matrisen.
• Den karakteristiska ekvationen för en tredje ordningens konstanta koefficienter eller Cauchy-Euler (jämviktiga variabelkoefficienter) linjär differentialekvation eller differensekvation är en kubisk ekvation.
• Skärningspunkterna mellan kubisk Bézier -kurva och rak linje kan beräknas med direkt kubikekvation som representerar Bézier -kurvan.
• Kritiska punkter i en kvartsfunktion hittas genom att lösa en kubisk ekvation (derivatuppsättningen lika med noll).
• Böjningspunkter för en kvintisk funktion är lösningen av en kubisk ekvation (den andra derivatuppsättningen lika med noll).

I andra vetenskaper

• Inom analytisk kemi kan Charlot -ekvationen , som kan användas för att hitta pH -värdet för buffertlösningar , lösas med en kubisk ekvation.
• I termodynamik är tillståndsekvationer (som relaterar tryck, volym och temperatur för ett ämne) kubiska i volymen.
• Kinematiska ekvationer som innefattar linjära accelerationshastigheter är kubik.
• Hastigheten på seismiska Rayleigh -vågor är en lösning av Rayleigh -vågens kubiska ekvation.

Anteckningar

Referenser

• Guilbeau, Lucye (1930), "The History of the Solution of the Cubic Equation", Mathematics News Letter , 5 (4): 8–12, doi : 10.2307/3027812 , JSTOR  3027812

Vidare läsning

• Anglin, WS; Lambek, Joachim (1995), "Mathematics in the Renaissance" , The Heritage of Thales , Springers, s. 125–131, ISBN 978-0-387-94544-6Ch. 24.
• Dence, T. (november 1997), "Cubics, chaos and Newton's method", Mathematical Gazette , Mathematical Association , 81 (492): 403–408, doi : 10.2307/3619617 , ISSN  0025-5572 , JSTOR  3619617
• Dunnett, R. (november 1994), "Newton – Raphson and the cubic", Mathematical Gazette , Mathematical Association , 78 (483): 347–348, doi : 10.2307/3620218 , ISSN  0025-5572 , JSTOR  3620218
• Jacobson, Nathan (2009), Basic algebra , 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1
• Mitchell, DW (november 2007), "Solving cubics by solving triangles", Mathematical Gazette , Mathematical Association , 91 : 514–516, doi : 10.1017/S0025557200182178 , ISSN  0025-5572
• Mitchell, DW (november 2009), "Powers of φ as roots of cubics", Mathematical Gazette , Mathematical Association , 93 , doi : 10.1017/S0025557200185237 , ISSN  0025-5572
• Tryck, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Avsnitt 5.6 Kvadratiska och kubiska ekvationer" , Numeriska recept: The Art of Scientific Computing (3: e upplagan), New York: Cambridge University Press, ISBN 978-0-521-88068-8
• Rechtschaffen, Edgar (juli 2008), "Real roots of cubics: Explicit formula for quasi-solutions", Mathematical Gazette , Mathematical Association , 92 : 268–276, doi : 10.1017/S0025557200183147 , ISSN  0025-5572
• Zucker, IJ (juli 2008), "The cubic equation-a new look at the irreducible case", Mathematical Gazette , Mathematical Association , 92 : 264–268, doi : 10.1017/S0025557200183135 , ISSN  0025-5572

externa länkar

• "Cardano formula" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Historia om kvadratiska, kubiska och kvartiska ekvationer på MacTutor -arkiv .
• 500 år av att INTE undervisa i KUBISK FORMULA. Vad tror de att du inte kan hantera? - YouTube -video av Mathologer om historien om kubikekvationer och Cardanos lösning, samt Ferraris lösning på kvartsekvationer