Kedjekomplex - Chain complex

I matematik är ett kedjekomplex en algebraisk struktur som består av en sekvens av abeliska grupper (eller moduler ) och en sekvens av homomorfismer mellan på varandra följande grupper så att bilden av varje homomorfism ingår i nästa kärna . Associerat till ett kedjekomplex är dess homologi , som beskriver hur bilderna ingår i kärnorna.

Ett kedjekomplex liknar ett kedjekomplex, förutom att dess homomorfier följer en annan konvention. Homologin för ett cochain-komplex kallas dess cohomology.

I algebraisk topologi konstrueras det singulära kedjekomplexet i ett topologiskt utrymme X med kontinuerliga kartor från en simplex till X, och kedjekomplexets homomorfier fångar upp hur dessa kartor begränsar sig till gränsen för simplex. Homologin för detta kedjekomplex kallas singular homology of X och är en vanligt förekommande invariant i ett topologiskt utrymme.

Kedjekomplex studeras i homologisk algebra , men används inom flera områden av matematik, inklusive abstrakt algebra , Galois-teori , differentiell geometri och algebraisk geometri . De kan definieras mer generellt i abeliska kategorier .

Definitioner

En kedja-komplex är en sekvens av abelian grupper eller moduler ..., A ₀ , A ₁ , A ₂ , A ₃ , A ₄ , ... anslutna genom homomorfismer (kallas gräns operatörer eller differentialer ) d _n : A _n → A _n₋₁ , så att sammansättningen av två kartor i följd är nollkartan. Skillnaderna uppfyller uttryckligen d _n ∘ d _n₊₁ = 0 , eller med index undertryckta, d ² = 0 . Komplexet kan skrivas ut enligt följande. ${\ displaystyle (A _ {\ bullet}, d _ {\ bullet})}$

{\ displaystyle \ cdots {\ xleftarrow {d_ {0}}} A_ {0} {\ xleftarrow {d_ {1}}} A_ {1} {\ xleftarrow {d_ {2}}} A_ {2} {\ xleftarrow {d_ {3}}} A_ {3} {\ xleftarrow {d_ {4}}} A_ {4} {\ xleftarrow {d_ {5}}} \ cdots}

Den cochain komplex är den dubbla tanken till en kedja komplex. Den består av en sekvens av abelian grupper eller moduler ..., A ⁰ , A ¹ , A ² , A ³ , A ⁴ , ... anslutna genom homomorfismer d ⁿ : A ⁿ → A ⁿ¹ uppfyller d ⁿ¹ ∘ d ⁿ = 0 . Cochain-komplexet kan skrivas ut på ett liknande sätt som kedjekomplexet. ${\ displaystyle (A ^ {\ bullet}, d ^ {\ bullet})}$

{\ displaystyle \ cdots {\ xrightarrow {d ^ {- 1}}} A ^ {0} {\ xrightarrow {d ^ {0}}} A ^ {1} {\ xrightarrow {d ^ {1}}} A ^ {2} {\ xrightarrow {d ^ {2}}} A ^ {3} {\ xrightarrow {d ^ {3}}} A ^ {4} {\ xrightarrow {d ^ {4}}} \ cdots}

Index n i antingen A _n eller A ⁿ refereras till som den grad (eller dimension ). Skillnaden mellan kedjekomplex och kedjekomplex är att skillnaderna i kedjekomplex minskar dimensionen, medan kedjekomplex ökar dimensionen. Alla begrepp och definitioner för kedjekomplex gäller för kedjekomplex, förutom att de följer denna olika konvention för dimension och ofta ges termer prefixet co- . I den här artikeln kommer definitioner att ges för kedjekomplex när skillnaden inte krävs.

Ett avgränsat kedjan komplex är ett i vilket nästan alla de A _n är 0; det vill säga ett ändligt komplex som utvidgas till vänster och höger med 0. Ett exempel är kedjekomplexet som definierar den enkla homologin för ett ändligt förenklat komplex . Ett kedjekomplex är avgränsat ovan om alla moduler över någon fast grad N är O, och avgränsas nedan om alla moduler under någon fast grad är 0. Det är uppenbart att ett komplex avgränsas både över och under om och endast om komplexet är avgränsat.

Elementen i de enskilda grupperna i ett (sam) kedjekomplex kallas (sam) kedjor . Elementen i kärnan i d kallas (co) cykler (eller slutna element), och elementen i bilden av d kallas (co) gränser (eller exakta element). Precis från definitionen av differentialen är alla gränser cykler. Den n : te (sam) homologi grupp H _n ( H ⁿ ) är den grupp av (sam) cykler modulo (sam) gränser i grad n , det vill säga,

{\ displaystyle H_ {n} = {\ frac {\ ker d_ {n}} {{\ mbox {im}} d_ {n + 1}}} \ quad \ left (H ^ {n} = {\ frac { \ ker d ^ {n}} {{\ mbox {im}} d ^ {n-1}}} höger)}

Exakta sekvenser

En exakt sekvens (eller exakt komplex) är ett kedjekomplex vars homologigrupper alla är noll. Detta betyder att alla slutna element i komplexet är exakta. En kort exakta sekvensen är en avgränsas exakt sekvens i vilken endast de grupper A _k , A _{k 1} , A _{k 2} kan vara skild från noll. Till exempel är följande kedjekomplex en kort exakt sekvens.

{\ displaystyle \ cdots {\ xrightarrow {}} \; 0 \; {\ xrightarrow {}} \; \ mathbf {Z} \; {\ xrightarrow {\ times p}} \; \ mathbf {Z} \ twoheadrightarrow \ mathbf {Z} / p \ mathbf {Z} \; {\ xrightarrow {}} \; 0 \; {\ xrightarrow {}} \ cdots}

I den mellersta gruppen är de slutna elementen elementen p Z ; dessa är helt klart de exakta elementen i denna grupp.

Kedjekartor

En kedjekarta f mellan två kedjekomplex och är en sekvens av homomorfismer för varje n som pendlar med gränsoperatorerna på de två kedjekomplexen, så . Detta skrivs ut i följande kommutativa diagram . ${\ displaystyle (A _ {\ bullet}, d_ {A, \ bullet})}$ ${\ displaystyle (B _ {\ bullet}, d_ {B, \ bullet})}$ ${\ displaystyle f _ {\ bullet}}$ ${\ displaystyle f_ {n}: A_ {n} \ rightarrow B_ {n}}$ ${\ displaystyle d_ {B, n} \ circ f_ {n} = f_ {n-1} \ circ d_ {A, n}}$

En kedjekarta skickar cykler till cykler och gränser till gränser och inducerar därmed en karta över homologi . ${\ displaystyle (f _ {\ bullet}) _ {*}: H _ {\ bullet} (A _ {\ bullet}, d_ {A, \ bullet}) \ rightarrow H _ {\ bullet} (B _ {\ bullet}, d_ {B, \ bullet})}$

En kontinuerlig karta f mellan topologiska rum X och Y inducerar en kedja karta mellan de singulära kedjan komplex av X och Y , och därmed inducerar en karta f _* mellan den singulära homologin för X och Y samt. När X och Y båda är lika med n- sfären definierar kartan inducerad av homologi graden av kartan f .

Begreppet kedjekarta minskar till gränsen genom konstruktionen av kedjekonens kon .

Kedjehomotopi

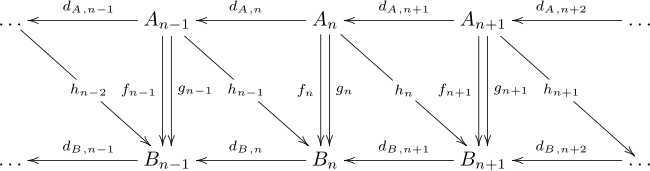
En kedjehomotopi erbjuder ett sätt att relatera två kedjekartor som inducerar samma karta på homologigrupper, även om kartorna kan vara olika. Med tanke på två kedjekomplex A och B och två kedjekartor f , g : A → B , är en kedjehomotopi en sekvens av homomorfismer h _n : A _n → B _{n +1} så att hd _A + d _B h = f - g . Kartorna kan skrivas ut i ett diagram enligt följande, men detta diagram är inte kommutativt.

Kartan hd _A + d _B h är lätt att verifiera för att inducera nollkartan på homologi, för alla h . Det följer omedelbart att f och g inducerar samma karta i homologin. Man säger att f och g är kedjehomotopiska (eller helt enkelt homotopiska ), och den här egenskapen definierar en ekvivalensrelation mellan kedjekartor.

Låt X och Y vara topologiska utrymmen. I fallet med singularhomologi inducerar en homotopi mellan kontinuerliga kartor f , g : X → Y en kedjehomotopi mellan kedjekartorna som motsvarar f och g . Detta visar att två homotopiska kartor inducerar samma karta i singular homologi. Namnet "chain homotopy" motiveras av detta exempel.

Exempel

Singular homologi

Låt X vara ett topologiskt utrymme. Definiera C _n ( X ) för att naturlig n ska vara den fria abeliska gruppen formellt genererad av singular n-enkelheter i X och definiera den gränsmapp som ska ${\ displaystyle \ partial _ {n}: C_ {n} (X) \ till C_ {n-1} (X)}$

{\ displaystyle \ partial _ {n}: \, (\ sigma: [v_ {0}, \ ldots, v_ {n}] \ to X) \ mapsto \ sum _ {i = 0} ^ {n} (- 1) ^ {i} (\ sigma: [v_ {0}, \ ldots, {\ hat {v}} _ {i}, \ ldots, v_ {n}] \ till X)}

där hatten utelämnar ett toppunkt . Det vill säga gränsen för en singular simplex är den alternerande summan av begränsningar för dess ansikten. Det kan visas att ∂ ² = 0, så är ett kedjekomplex; den singulär homologi är homologin av detta komplex. ${\ displaystyle (C _ {\ bullet}, \ partial _ {\ bullet})}$ ${\ displaystyle H _ {\ bullet} (X)}$

Singular homologi är en användbar invariant av topologiska utrymmen upp till homotopiekvivalens . Graden noll homologi gruppen är en fri abelsk grupp på väg-komponenterna av X .

de Rham kohomologi

Den differentiella k -formerna på någon slät grenröret M bildar en verklig vektorrum kallas Ω ^k ( M ) under tillsatsen. Det yttre derivatet d kartlägger Ω ^k ( M ) till Ω ^{k +1} ( M ), och d ² = 0 följer väsentligen från symmetri av andra derivat , så vektorutrymmena för k- formar tillsammans med det yttre derivatet är ett cochain-komplex.

{\ displaystyle \ Omega ^ {0} (M) \ {\ stackrel {d} {\ to}} \ \ Omega ^ {1} (M) \ to \ Omega ^ {2} (M) \ to \ Omega ^ {3} (M) \ till \ cdots}

Den Snittkohomologi av detta komplex kallas de rhamkohomologi av X . Homologin gruppen i dimension noll är isomorf med rymdvektor av lokalt konstanta funktioner från M till R . Sålunda för en kompakt grenrör, detta är den verkliga rymdvektor vars dimension är antalet anslutna komponenter hos M .

Släta kartor mellan grenrör inducerar kedjekartor, och släta homotopier mellan kartor inducerar kedjehomotopier.

Kategori av kedjekomplex

Kedjekomplex av K- moduler med kedjekartor bildar en kategori Ch _K , där K är en kommutativ ring.

Om V = V och W = W är kedjekomplex är deras tensorprodukt ett kedjekomplex med grad n- element som ges av ${\ displaystyle {} _ {*}}$ ${\ displaystyle {} _ {*}}$ ${\ displaystyle V \ otimes W}$

{\ displaystyle (V \ otimes W) _ {n} = \ bigoplus _ {\ {i, j | i + j = n \}} V_ {i} \ otimes W_ {j}}

och differentiell som ges av

{\ displaystyle \ partial (a \ otimes b) = \ partial a \ otimes b + (- 1) ^ {\ left | a \ right |} a \ otimes \ partial b}

där a och b är två homogena vektorer i V respektive W , och betecknar graden a . ${\ displaystyle \ left | a \ right |}$

Denna tensorprodukt gör kategorin Ch _K till en symmetrisk monoid kategori . Identitetsobjektet med avseende på denna monoida produkt är basringen K betraktad som ett kedjekomplex i grad 0. Flätningen ges på enkla tensorer av homogena element av

{\ displaystyle a \ otimes b \ mapsto (-1) ^ {\ left | a \ right | \ left | b \ right |} b \ otimes a}

Tecknet är nödvändigt för att flätningen ska vara en kedjekarta.

Dessutom har kategorin av kedjekomplex av K- moduler också inre Hom : givna kedjekomplex V och W , det inre Hom av V och W , betecknat Hom ( V , W ), är kedjekomplexet med grad n- element som ges av och differentiell som ges av ${\ displaystyle \ Pi _ {i} {\ text {Hom}} _ {K} (V_ {i}, W_ {i + n})}$