Vägbredd - Pathwidth

I grafteori , en väg nedbrytning av en graf G är informellt, en representation av G som en "förtjockad" väg diagram och pathwidth av G är ett nummer som mäter hur mycket vägen var förtjockade att bilda G . Mer formellt är en vägnedbrytning en sekvens av delmängder av G- hörn så att slutpunkterna för varje kant visas i en av delmängderna och så att varje toppunkt visas i en sammanhängande följd av delmängderna, och vägbredden är en mindre än storleken på den största uppsättningen i en sådan sönderdelning. Pathwidth är också känd som intervall tjocklek (en mindre än det maximala klick storlek i ett intervall supergraph av G ), vertex separationsnummer , eller nod sökningsnummer .

Vägbredd och nedbrytning av vägar är nära analoga med nedbrytning av trädbredd och träd . De spelar en nyckelroll i teorin om mindreåriga : familjerna till grafer som är stängda under mindreåriga och inte inkluderar alla skogar kan karakteriseras som att de har begränsad vägbredd och "virvlarna" som förekommer i den allmänna strukturteorin för mindre- stängda diagramfamiljer har begränsat vägbredd. Pathwidth, och grafer över begränsad pathwidth, har också tillämpningar inom VLSI- design, grafritning och beräkningslingvistik .

Det är NP-svårt att hitta vägbredden för godtyckliga grafer, eller till och med att approximera den exakt. Problemet är emellertid en fast parameter som kan hanteras : att testa om en graf har banbredd k kan lösas på en tid som beror linjärt på storleken på diagrammet men superexponentiellt på k . Dessutom, för flera speciella klasser av grafer, såsom träd , kan vägbredden beräknas i polynomtid utan beroende av k . Många problem i grafalgoritmer kan lösas effektivt på grafer med avgränsad banbredd genom att använda dynamisk programmering vid en bannedbrytning av grafen. Bannedbrytning kan också användas för att mäta rymdkomplexiteten hos dynamiska programmeringsalgoritmer på grafer med avgränsad träbredd .

Definition

Ett exempel på diagram G med banbredd 2 och dess vägnedbrytning av bredd 2. Bildens nedre del är samma graf och bannedbrytning med färg som läggs till för betoning. (Detta exempel är en anpassning av diagrammet som presenteras i, betoning lagt till)

I den första av sina berömda pappersserier om mindreåriga , definierar Neil Robertson och Paul Seymour ( 1983 ) en vägnedbrytning av en graf G för att vara en sekvens av delmängder X _i hörn av G , med två egenskaper:

För varje kant av G , det finns ett i sådant att båda ändpunkter kanten tillhör undergrupp X _i , och
För vart tredje index i ≤ j ≤ k , X _i ∩ X _k ⊆ X _j .

Den andra av dessa två egenskaper är ekvivalent med att kräva att delmängderna som innehåller ett visst toppunkt bildar en sammanhängande följd av hela sekvensen. På de senare tidningarna i Robertson och Seymours grafminorserie är en vägnedbrytning en trädnedbrytning ( X , T ) där det bakomliggande trädet T för nedbrytningen är en bandiagram .

Bredden på en vägnedbrytning definieras på samma sätt som för trädnedbrytning, som max _i | X _i | - 1, och pathwidth av G är bredden på någon väg-sönderdelning av minst G . Subtraktion av en från storleken på Xi _i denna definition gör liten skillnad i de flesta tillämpningar av banbredd, men används för att göra banbredden för ett bandiagram lika med ett.

Alternativa karakteriseringar

Som Bodlaender (1998) beskriver kan vägbredd karakteriseras på många likvärdiga sätt.

Limningssekvenser

En bana sönderdelning kan beskrivas som en sekvens av grafer G _i att limmas ihop genom att identifiera par av hörn från konsekutiva grafer i sekvensen, så att resultatet av att utföra alla dessa gluings är G . Kurvorna G _jag kan tas som de inducerade subgrafer i uppsättningarna X _i i den första definitionen av path sönderdelningar, med två hörn i successiva inducerade subgrafer som limmas ihop när de induceras av samma hörn i G , och i den andra riktningen man kan återhämta sig uppsättningarna X _jag som vertex uppsättningar av kurvorna G _i . Bredden på banan nedbrytningen är då ett mindre än det maximala antalet hörn i en av graferna G _i .

Intervalltjocklek

Ett intervalldiagram med vägbredd två, en mindre än kardinaliteten för dess fyra maximala klick ABC , ACD , CDE och CDF .

Banbredden för ett diagram G är lika med ett mindre än det minsta klickantalet i ett intervalldiagram som innehåller G som ett subgraf. Det vill säga, för varje bannedbrytning av G kan man hitta ett intervallsupergraf av G , och för varje intervall supergraf av G kan man hitta en bannedbrytning av G , så att nedbrytningens bredd är en mindre än klickantalet på intervalldiagram.

Antag att en vägnedbrytning av G ges i en riktning. Då kan man representera sönderdelningens noder som punkter på en linje (i banordning) och representera varje toppunkt v som ett slutet intervall med dessa punkter som slutpunkter. På detta sätt motsvarar vägnedbrytningsnoder som innehåller v motsvarande punkter i intervallet för v . Den skärnings graf av intervallen bildade från hörnen av G är ett intervall graf som innehåller G som en subgraf. Dess maximala klickarna ges av uppsättningarna av intervall innehållande de representativa punkter, och dess maximala klick storlek är en plus pathwidth av G .

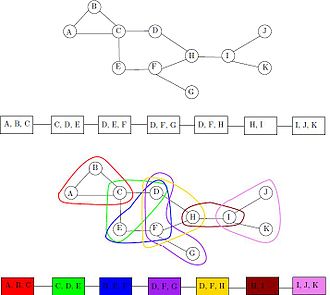
I den andra riktningen, om G är en subgraf av ett intervalldiagram med klickantal p + 1, har G en bannedbrytning av bredd p vars noder ges av de maximala klickarna i intervalldiagrammet. Exempelvis har intervalldiagrammet som visas med dess intervallrepresentation i figuren en vägnedbrytning med fem noder, motsvarande dess fem maximala klick ABC , ACD , CDE , CDF och FG ; den maximala klickstorleken är tre och bredden på denna vägnedbrytning är två.

Denna ekvivalens mellan vägbredd och intervalltjocklek är nära analog med ekvivalensen mellan trebredd och minsta klickantal (minus en) i ett ackorddiagram, av vilket den angivna grafen är en subgraf. Intervalldiagram är ett speciellt fall av ackorddiagram, och ackorddiagram kan representeras som korsningsdiagram för underträd i ett vanligt träd som generaliserar hur intervalldiagram är korsningsdiagram för delvägar till en bana.

Vertex separationsnummer

Antag att topparna i ett diagram G är linjärt ordnade . Då är vertex-separationsantalet G det minsta antalet s så att för varje vertex v , högst s- hörn är tidigare än v i ordningen men som har v eller ett senare hörn som granne. Vertex separations antalet G är det lägsta vertex separations antal av någon linjär ordning av G . Vertex separationsnummer definierades av Ellis, Sudborough & Turner (1983) , och är lika med den pathwidth av G . Detta följer av den tidigare ekvivalensen med intervallgrafklicknummer: om G är en undergraf av ett intervalldiagram I , representerad (som i figuren) på ett sådant sätt att alla intervalländpunkter är distinkta, då ordningen av de vänstra ändpunkterna för intervall i har vertex separation nummer ett mindre än klick antalet jag . Och i den andra riktningen kan man från en linjär ordning av G härleda en intervallrepresentation där den vänstra ändpunkten för intervallet för ett toppunkt v är dess position i ordningen och den högra ändpunkten är positionen för grannen till v som kommer sist i beställningen.

Nodsökningsnummer

Nodsökningsspelet i en graf är en form av strävan att undvika där en uppsättning sökare samarbetar för att spåra en flyktig gömd i en graf. Sökarna placeras på kurvorna i diagrammet medan den flyktande kan befinna sig i vilken kant av grafen som helst och flyktingens plats och rörelser är dolda för sökarna. I varje tur kan några eller alla sökare röra sig (godtyckligt, inte nödvändigtvis längs kanter) från ett toppunkt till ett annat, och sedan kan flyktingen röra sig längs vilken väg som helst i diagrammet som inte passerar genom ett sökarupptaget toppunkt. Flyktingen fångas när båda slutpunkterna i hans kant ockuperas av sökare. Nodsökningsnumret i en graf är det minsta antal sökare som behövs för att säkerställa att flyktingen kan garanteras fångas, oavsett hur han rör sig. Som Kirousis & Papadimitriou (1985) visar är nodsökningsnumret i en graf lika med dess intervalltjocklek. Den optimala strategin för sökarna är att flytta sökarna så att de i på varandra följande vändningar bildar separationsuppsättningarna i en linjär ordning med minimalt vertex-separationsnummer.

Gräns

Ett larvträd , en maximal graf med vägbredd.

Varje n -vertex graf med pathwidth k har som mest k ( n - k + ( k - 1) / 2) kanter, och den maximala pathwidth- k grafer (grafer till vilket ingen fler kanter kan läggas utan att öka pathwidth) har exakt så många kanter. En maximal pathwidth- k kurva måste vara antingen en k -path eller k -caterpillar två speciella typer av k -träd. Ett k- träd är ett ackorddiagram med exakt n - k maximala klick , var och en innehållande k + 1 hörn; i ett k- träd som inte i sig är en ( k + 1) -klick , separerar varje maximal klick antingen diagrammet i två eller flera komponenter, eller så innehåller den ett enda blad, en topp som bara tillhör en enda maximal klick. En k- stig är ett k- träd med högst två blad, och en k- kateral är ett k- träd som kan delas upp i en k- stig och en uppsättning k- löv vardera intill en separator k- klick av den k -path. I synnerhet är de maximala kurvorna för vägbredd en exakt larvträd .

Eftersom vägnedbrytning är ett speciellt fall av nedbrytning av träd, är banbredden för vilken graf som helst större än eller lika med dess trebredd . Banbredden är också mindre än eller lika med skärbredden , det minsta antalet kanter som korsar varje skärning mellan lägre och högre numrerade toppar i ett optimalt linjärt arrangemang av kurvorna i en graf; detta följer eftersom toppseparationsnumret, antalet lägre numrerade toppar med högre numrerade grannar, högst kan motsvara antalet kapade kanter. Av liknande skäl är skärbredden högst vägbredden gånger den maximala graden för hörn i en given graf.

Varje n- vertikal skog har vägbredd O (log n ). För i en skog kan man alltid hitta ett konstant antal hörn vars avlägsnande lämnar en skog som kan delas in i två mindre underskogar med högst 2 n / 3 hörn vardera. Ett linjärt arrangemang bildat genom att rekursivt partitionera var och en av dessa två underskogar, placera de separerande topparna mellan dem, har logaritmiskt vertexsökningsnummer. Samma teknik, tillämpad på en trädnedbrytning av en graf, visar att om trebredden för ett n- vertikalt diagram G är t , så är banbredden för G O ( t log n ). Eftersom yttre plana grafer , serie – parallella grafer och Halin-grafer alla har avgränsat trebredd har de alla också högst logaritmisk banbredd.

Samt dess förbindelser till treewidth är pathwidth också relaterad till clique-bredd och cutwidth , via linjediagram ; linjediagrammet L ( G ) för en graf G har ett toppunkt för varje kant av G och två hörn i L ( G ) ligger intill när motsvarande två kanter av G delar en slutpunkt. Varje familj av grafer har avgränsat banbredd om och endast om dess linjediagram har avgränsat linjär klickbredd, där linjär klickbredd ersätter den ojämna sammanslutningsoperationen från klickbredd med funktionen att angränsa till en enda ny topp. Om en ansluten graf med tre eller flera hörn har maximal grad tre, är dess skärbredd lika med vertexseparationsnumret för linjediagrammet.

I alla plana diagram är vägbredden högst proportionell mot kvadratroten av antalet hörn. Ett sätt att hitta en vägnedbrytning med denna bredd är (på samma sätt som den logaritmiska breddens nedbrytning av skogar som beskrivs ovan) att använda den plana avskiljningssatsen för att hitta en uppsättning O ( √ n ) vertikaler vars avlägsnande skiljer grafer i två underbilder med högst 2 n / 3 hörn vardera och sammanfoga rekursivt konstruerade bannedbrytningar för vart och ett av dessa två underbilder. Samma teknik gäller för alla klasser av diagram som en liknande avgränsningssats har. Eftersom graferna i alla fasta mindre stängda graffamiljer, som plana grafer, har separatorer av storlek O ( √ n ), följer det att kurvens vägbredd i en fast mindre stängd familj igen är O ( √ n ). För vissa klasser av plana grafer måste kurvens vägbredd och banbredden för dess dubbla graf ligga inom en konstant faktor av varandra: gränser för denna form är kända för tvåanslutna yttre plana grafer och för polyhedrala grafer. För 2-anslutna plana grafer är banbredden för den dubbla grafen mindre än banbredden för linjediagrammet. Det förblir öppet huruvida en plan graf och dess dubbla alltid är inom en konstant faktor av varandra i de återstående fallen.

I vissa klasser av grafer har det bevisats att vägbredden och trebredden alltid är lika med varandra: detta gäller för grafer , permutationsdiagram , komplement till jämförbarhetsdiagram och jämförbarhetsdiagram för intervallordningar .

Olöst problem i matematik :

Vad är den största möjliga banbredden för en kubisk graf i en vertikal ? ${\ displaystyle n}$

(mer olösta problem i matematik)

I vilket kubiskt diagram som helst , eller mer generellt i ett diagram med maximal vertexgrad tre, är banbredden högst n / 6 + o ( n ), där n är antalet hörn i diagrammet. Det finns kubiska diagram med vägbredd 0,082 n , men det är inte känt hur man kan minska detta gap mellan denna nedre gräns och den övre gränsen n / 6.

Beräkning av vägnedbrytning

Det är NP-komplett för att avgöra om banbredden för en given graf högst är k , när k är en variabel som ges som en del av ingången. De mest kända värsta fallgränserna för beräkning av vägbredden för godtyckliga n- vertikala grafer är av formen O (2 ⁿ n ^c ) för någon konstant c . Icke desto mindre är flera algoritmer kända för att beräkna vägnedbrytningar mer effektivt när vägbredden är liten, när klassen av inmatningsdiagram är begränsad eller ungefär.

Färdiga parametrar

Pathwidth är en fast parameter som kan spåras : för alla konstanta k är det möjligt att testa om pathwidth är högst k , och om så är fallet att hitta en bannedbrytning av bredden k , i linjär tid. I allmänhet fungerar dessa algoritmer i två faser. I den första fasen används antagandet att grafen har vägbredd k för att hitta en vägnedbrytning eller trädnedbrytning som inte är optimal men vars bredd kan begränsas som en funktion av k . I den andra fasen tillämpas en dynamisk programmeringsalgoritm på denna sönderdelning för att hitta optimal sönderdelning. Emellertid, de tids gränserna för kända algoritmer av denna typ är exponentiell i k ² , opraktisk utom för de minsta värdena av k . För fallet k = 2 ges en uttrycklig linjär tidsalgoritm baserad på en strukturell sönderdelning av banbredd-2-grafer av de Fluiter (1997) .

Särskilda klasser av grafer

Bodlaender (1994) harvtxt-fel: flera mål (2 ×): CITEREFBodlaender1994 ( hjälp ) undersöker komplexiteten i att beräkna vägbredden på olika specialklasser av grafer. Att avgöra om sökvägen för ett diagram G högst är k förblir NP-komplett när G är begränsad till avgränsade grafer, plana grafer , plana grafer med avgränsad grad, ackorddiagram , ackorddominoer, komplement till jämförbarhetsdiagram och avstånd från två delar ärftliga grafer . Det följer omedelbart att det också är NP-komplett för graffamiljerna som innehåller tvåpartsavstånds-ärftliga grafer, inklusive tvåpartsdiagram, ackordbipartitdiagram, avstånd-ärftliga grafer och cirkeldiagram .

Dock kan vägbredden beräknas linjärt för träd och skogar. Det kan också beräknas i polynomtid för grafer med avgränsad trebredd inklusive serie – parallella grafer , yttre plana grafer och Halin-grafer , liksom för delade grafer , för komplement till ackorddiagram, för permutationsdiagram , för grafer , för cirkulära- bågediagram , för jämförbarhetsdiagrammen för intervallordningar och naturligtvis för själva intervalldiagram , eftersom i så fall är banbredden bara en mindre än det maximala antalet intervall som täcker någon punkt i en intervallrepresentation av grafen.

Ungefärliga algoritmer

Det är NP-svårt att approximera kurvens vägbredd till en additivkonstant. Det mest kända approximationsförhållandet för en polynom-tids approximationsalgoritm för banbredd är O ((log n ) ^3/2 ). För tidigare approximeringsalgoritmer för banbredd, se Bodlaender et al. (1992) och Guha (2000) . För approximationer för begränsade klasser av grafer, se Kloks & Bodlaender (1992) .

Mindreåriga

En mindre av ett diagram G är en annan graf som bildas av G genom att dra ihop kanter, ta bort kanter och ta bort hörn. Mindreåriga har en djup teori där flera viktiga resultat involverar vägbredd.

Exkluderar en skog

Om en familj F av diagram stängs under åtagande av minderåriga (varje minderårig av en medlem av F är också i F ), så kan satsen F av Robertson – Seymour karakteriseras som graferna som inte har någon mindre i X , där X är en begränsad uppsättning förbjudna minderåriga . Till exempel säger Wagners teorem att de plana graferna är de grafer som varken har hela grafen K ₅ eller den fullständiga bipartitgrafen K _3,3 som minderåriga. I många fall är egenskaperna hos F och egenskaperna hos X nära besläktade, och det första resultatet av denna typ var av Robertson & Seymour (1983) och relaterar avgränsad vägbredd med förekomsten av en skog i familjen förbjudna minderåriga . Definiera specifikt en familj F av grafer som har avgränsad vägbredd om det finns en konstant p så att varje graf i F har högst vägbredd p . Sedan har en mindre stängd familj F begränsat banbredden om och bara om uppsättningen X av förbjudna minderåriga för F innehåller minst en skog.

I en riktning är detta resultat enkelt att bevisa: om X inte innehåller minst en skog, har de X- mindre fria graferna inte begränsad banbredd. För i det här fallet inkluderar de X- mindre fria graferna alla skogar, och i synnerhet inkluderar de perfekta binära träd . Men ett perfekt binärt träd med 2 k + 1-nivåer har vägbredd k , så i detta fall har X -minor-fria grafer obegränsad sökbredd. I den andra riktningen, om X innehåller en n- vertikal skog, har de X- minderfria graferna högst vägbredd n - 2.

Hinder för begränsad banbredd

De förbjudna minderåriga för kurvor för vägbredd 1.

Egenskapen med att ha en vägbredd som mest p är i sig stängd under åtagande av minderåriga: om G har en vägnedbrytning med bredden högst p , förblir samma vägnedbrytning giltig om någon kant avlägsnas från G och varje topp kan avlägsnas från G och från dess nedbrytning utan att öka bredden. Kontraktion av en kant kan också åstadkommas utan att bryta sönderdelningens bredd genom att slå samman delvägarna som representerar de två slutpunkterna för den kontraherade kanten. Därför, de grafer av pathwidth högst p kan kännetecknas av en uppsättning X _p över uteslutna minderåriga.

Även om X _p innefattar nödvändigtvis minst en skog, är det inte sant att alla grafer i X _p är skogar: till exempel, X ₁ består av två grafer, en sju-vertex trädet och triangeln K ₃ . Träduppsättningen i X _p kan emellertid exakt karaktäriseras: dessa träd är exakt de träd som kan bildas av tre träd i X _{p - 1} genom att ansluta ett nytt rotpunktskant med en kant till ett godtyckligt valt toppspets i vart och ett av tre mindre träd. Till exempel bildas sju-vertex-trädet i X ₁ på detta sätt från två-vertex-trädet (en enda kant) i X ₀ . Baserat på denna konstruktion kan antalet förbjudna minderåriga i X _p visas att vara minst ( p !) ² . Hela uppsättningen X ₂ av förbjudna minderåriga för kurvor för vägbredd-2 har beräknats; den innehåller 110 olika grafer.

Strukturteori

Den grafstruktur theorem för mindre-sluten graf familjer anges att, för varje sådan familj F , kurvorna i F kan delas upp i klicksummor av grafer som kan inbäddade på ytor av avgränsas släktet , tillsammans med en begränsad antal spetsar och virvlar för varje komponent i klicksumman. En topp är ett toppunkt som kan ligga intill vilket annat toppunkt som helst i dess komponent, medan en virvel är en graf över avgränsad banbredd som limmas in i en av ansiktena på det avgränsade släktets inbäddning av en komponent. Den cykliska ordningen av topparna runt ansiktet i vilken en virvel är inbäddad måste vara kompatibel med virvelnedbrytning av virveln, i den meningen att bryta cykeln för att bilda en linjär ordning måste leda till en ordning med avgränsat vertexseparationsnummer. Denna teori, där vägbredd är nära kopplad till godtyckliga mindre stängda graffamiljer, har viktiga algoritmiska applikationer.

Applikationer

VLSI

I VLSI- design studerades vertexseparationsproblemet ursprungligen som ett sätt att dela kretsar i mindre delsystem, med ett litet antal komponenter på gränsen mellan delsystemen.

Ohtsuki et al. (1979) använder intervalltjocklek för att modellera antalet spår som behövs i en endimensionell layout för en VLSI-krets, bildad av en uppsättning moduler som behöver sammankopplas av ett nätsystem. I sin modell bildar man ett diagram där vertikalerna representerar nät och i vilka två vertikaler är förbundna med en kant om deras nät båda ansluter till samma modul; det vill säga om modulerna och näten tolkas som att de bildar noderna och hyperkanterna för en hypergraf, så är grafen som bildas av dem dess linjediagram . En intervallrepresentation av en supergraf av denna linjediagram, tillsammans med en färgning av supergrafen, beskriver ett arrangemang av näten längs ett system med horisontella spår (ett spår per färg) på ett sådant sätt att modulerna kan placeras längs spåren i linjär ordning och anslut till lämpliga nät. Det faktum att intervalldiagram är perfekta diagram innebär att antalet färger som behövs, i ett optimalt arrangemang av denna typ, är samma som klickantalet för intervallets slutförande av nätdiagrammet.

Portmatrislayout är en specifik stil för CMOS VLSI-layout för booleska logiska kretsar. I grindmatrislayouter förökas signaler längs "linjer" (vertikala linjesegment) medan varje grind i kretsen bildas av en sekvens av anordningsegenskaper som ligger längs ett horisontellt linjesegment. Således måste det horisontella linjesegmentet för varje grind korsa de vertikala segmenten för var och en av de linjer som bildar in- eller utgångar från grinden. Som i layouterna av Ohtsuki et al. (1979) , en layout av denna typ som minimerar antalet vertikala spår på vilka linjerna ska ordnas kan hittas genom att beräkna banbredden för en graf som har linjerna som sina hörn och par av linjer som delar en grind som sin kanter. Samma algoritmiska tillvägagångssätt kan också användas för att modellera vikproblem i programmerbara logiska matriser .

Diagramritning

Pathwidth har flera applikationer för att rita ritningar :

De minimala graferna som har ett visst korsningsnummer har sökbredd som begränsas av en funktion av deras korsningsnummer.
Antalet parallella linjer på vilka ett träds hörn kan dras utan kantkorsningar (under olika naturliga begränsningar för hur intilliggande hörn kan placeras med avseende på linjesekvensen) är proportionellt med trädets vägbredd.
En k- korsning av h- skikt av en graf G är en placering av G- hörnens på h distinkta horisontella linjer, med kanter dirigerade som monotona polygonala banor mellan dessa linjer, på ett sådant sätt att det högst finns k- korsningar. Diagrammen med sådana ritningar har banbredd som begränsas av en funktion av h och k . Därför, när både h och k är konstanta, är det möjligt i linjär tid att avgöra om ett diagram har en k- korsning av h- skikt.
En graf med n hörn och banbredd p kan inbäddas i ett tredimensionellt rutnät av storlek p × p × n på ett sådant sätt att inga två kanter (representerade som raka linjesegment mellan rutnätpunkter) skär varandra. Således har grafer över begränsad banbredd inbäddningar av denna typ med linjär volym.

Kompilator design

Vid sammanställningen av programmeringsspråk på hög nivå uppstår sökbredd i problemet med att ordna om sekvenser av linjär kod (det vill säga kod utan kontrollflödesgrenar eller slingor) på ett sådant sätt att alla värden som beräknas i koden kan placeras i maskinregister istället för att behöva spillas i huvudminnet. I den här applikationen representerar en koden som ska kompileras som en riktad acyklisk graf i vilken noderna representerar ingångsvärdena till koden och de värden som beräknas av operationerna i koden. En kant från nod x till nod y i denna DAG representerar det faktum att värdet x är en av ingångarna till operation y . En topologisk ordning av hörnpunkterna i denna DAG representerar en giltig omordning av koden, och antalet register som behövs för att utvärdera koden i en given ordning ges av ordningens vertekseparationsnummer.

För vilket fast antal w maskinregister som helst är det möjligt att bestämma linjärt om en bit linjär kod kan ordnas om på ett sådant sätt att den kan utvärderas med högst w- register. För, om toppunktavskiljningsnumret för en topologisk ordning är högst w , kan den minsta vertekseparationen mellan alla ordningar inte vara större, så den riktade grafen som bildas genom att ignorera riktningarna för DAG som beskrivs ovan måste ha en bana med högst w . Det är möjligt att testa om detta är fallet med de kända algoritmerna för fasta parametrar som kan spåras för vägbredd, och om så är fallet att hitta en vägnedbrytning för den riktade grafen, i linjär tid med tanke på antagandet att w är en konstant. När en vägsnedbrytning har hittats kan en topologisk ordning av bredden w (om en finns) hittas med hjälp av dynamisk programmering, återigen i linjär tid.

Lingvistik

Kornai & Tuza (1992) beskriver en tillämpning av vägbredd i naturlig språkbehandling . I den här applikationen modelleras meningar som diagram, där hörnpunkterna representerar ord och kanterna representerar förhållanden mellan ord; till exempel om ett adjektiv ändrar ett substantiv i meningen så skulle grafen ha en kant mellan dessa två ord. På grund av den begränsade kapaciteten hos det mänskliga korttidsminnet hävdar Kornai och Tuza att den här grafen måste ha begränsat vägbredd (mer specifikt hävdar de, högst sex vägbredder), för annars skulle människor inte kunna analysera tal korrekt.

Exponentiella algoritmer

Många problem i grafalgoritmer kan lösas effektivt på grafer med låg banbredd, genom att använda dynamisk programmering vid en bannedbrytning av grafen. Till exempel, om en linjär ordning av hörnpunkterna i en n- vertikalgraf G ges, med vertexseparationsnummer w , är det möjligt att hitta den maximala oberoende uppsättningen G i tid O (2 ^w n ). På grafer över begränsad sökbredd leder detta tillvägagångssätt till algoritmer med fasta parametrar, parametriserade av sökbredden. Sådana resultat återfinns inte ofta i litteraturen eftersom de sammanfattas av liknande algoritmer parametriserade av träbredden. emellertid uppstår vägbredd även i trebreddsbaserade dynamiska programmeringsalgoritmer vid mätning av rymdkomplexiteten hos dessa algoritmer.

Samma dynamiska programmeringsmetod kan också tillämpas på grafer med obegränsad banbredd, vilket leder till algoritmer som löser oparametrierade grafproblem under exponentiell tid . Att till exempel kombinera detta dynamiska programmeringssätt med det faktum att kubiska grafer har vägbredd n / 6 + o ( n ) visar att den maximala oberoende uppsättningen i en kubisk graf kan konstrueras i tid O (2 ^{n / 6 + o ( n )} ), snabbare än tidigare kända metoder. Ett liknande tillvägagångssätt leder till förbättrade exponentiella tidsalgoritmer för maximal klippning och minimala dominerande uppsättningsproblem i kubiska diagram och för flera andra NP-hårda optimeringsproblem.

Se även

Boxicitet , ett annat sätt att mäta komplexiteten hos en godtycklig graf i termer av intervalldiagram
Träddjup , ett tal som är begränsat till en mindre stängd graffamilj om och endast om familjen utesluter en sökväg
Degeneracy , ett mått på sparsiteten i en graf som högst är lika med dess banbredd
Grafbandbredd , ett annat NP-komplett optimeringsproblem med linjära layouter av grafer
Strahler-nummer , ett mått på komplexiteten hos rotade träd som definieras på samma sätt som stigbredden hos orörda träd

Anteckningar

Referenser

Alon, Noga ; Seymour, Paul ; Thomas, Robin (1990), "En separatorsats för grafer med en utesluten minor och dess tillämpningar", Proc. 22: e ACM-symp. on Theory of Computing (STOC 1990) , s. 293–299, doi : 10.1145 / 100216.100254 , ISBN 0897913612, S2CID 17521329.
Amini, Omid; Huc, Florian; Pérennes, Stéphane (2009), "On the path-width of planar grafer", SIAM Journal on Discrete Mathematics , 23 (3): 1311–1316, doi : 10.1137 / 060670146.
Arnborg, Stefan (1985), "Effektiva algoritmer för kombinatoriska problem på grafer med begränsad nedbrytbarhet - En undersökning", BIT , 25 (1): 2–23, doi : 10.1007 / BF01934985 , S2CID 122263659.
Arnborg, Stefan; Corneil, Derek G .; Proskurowski, Andrzej (1987), "Komplexitet för att hitta inbäddningar i ett $k-$ träd", SIAM Journal on Algebraic and Discrete Methods , 8 (2): 277–284, doi : 10.1137 / 0608024.
Aspvall, Bengt; Proskurowski, Andrzej; Telle, Jan Arne (2000), "Minneskrav för bords beräkningar i partiell k -träd algoritmer", Algorithmica , 27 (3): 382-394, doi : 10,1007 / s004530010025 , S2CID 9.690.525.
Berge, Claude (1967), "Några klasser av perfekta grafer", Grafteori och teoretisk fysik , New York: Academic Press, s. 155–165.
Bienstock, Dan; Robertson, Neil ; Seymour, Paul ; Thomas, Robin (1991), "Snabbt exkluderar en skog", Journal of Combinatorial Theory, serie B , 52 (2): 274–283, doi : 10.1016 / 0095-8956 (91) 90068-U.
Björklund, Andreas; Husfeldt, Thore (2008), "Exakt algoritmer för exakt satisfierbarhet och antal perfekta matchningar" Algorithmica , 52 (2): 226-249, doi : 10,1007 / s00453-007-9149-8 , S2CID 37.693.881.
Bodlaender, Hans L. (1994), "En turistguide genom trädbredd", i Dassow, Jürgen; Kelemenová, Alisa (red.), Utvecklingen inom teoretisk datavetenskap (Proc. 7: e internationella mötet för unga datavetare, Smolenice, 16–20 november 1992) , Ämnen i datematematik, 6 , Gordon and Breach, s. 1–20.
Bodlaender, Hans L. (1996), "En linjär tidsalgoritm för att hitta trädnedbrytning av liten trädbredd", SIAM Journal on Computing , 25 (6): 1305–1317, doi : 10.1137 / S0097539793251219 , hdl : 1874/16670.
Bodlaender, Hans L. (1998), "A partial k- barboretum of charts with bounded treewidth", Theoretical Computer Science , 209 (1–2): 1–45, doi : 10.1016 / S0304-3975 (97) 00228-4.
Bodlaender, Hans L .; Fomin, Fedor V. (2002), "tillnärmning av pathwidth av outerplanar grafer", Journal of Algorithms , 43 (2): 190-200, doi : 10,1016 / S0196-6774 (02) 00.001-9.
Bodlaender, Hans L .; Gilbert, John R .; Hafsteinsson, Hjálmtýr; Kloks, Ton (1992), "Approximating treewidth, pathwidth, and minimum elimination tree height", Graph-Theoretic Concepts in Computer Science , Lecture Notes in Computer Science , 570 , s. 1–12, doi : 10.1007 / 3-540- 55121-2_1 , hdl : 1874/17927 , ISBN 978-3-540-55121-8.
Bodlaender, Hans L .; Gustedt, Jens; Telle, Jan Arne (1998), "Linjetidsregistrering för ett fast antal register", Proc. 9: e ACM – SIAM-symposiet om diskreta algoritmer (SODA '98) (PDF) , s. 574–583.
Bodlaender, Hans L .; Kloks, Ton (1996), "Effektiva och konstruktiva algoritmer för pathwidth och treewidth av grafer", Journal of Algorithms , 21 (2): 358-402, doi : 10,1006 / jagm.1996.0049 , hdl : 1874/16538.
Bodlaender, Hans L .; Kloks, Ton; Kratsch, Dieter (1993), "Trewidth and pathwidth of permutation charts", Proc. 20th International Colloquium on Automata, Languages and Programming (ICALP 1993) , Lecture Notes in Computer Science, 700 , Springer-Verlag, s. 114–125, doi : 10.1007 / 3-540-56939-1_66 , hdl : 1874/16657 , ISBN 978-3-540-56939-8.
Bodlaender, Hans L .; Möhring, Rolf H. (1990), "Cografernas vägbredd och trebredd", Proc. 2: a Scandinavian Workshop on Algorithm Theory , Lecture Notes in Computer Science, 447 , Springer-Verlag, s. 301–309, doi : 10.1007 / 3-540-52846-6_99 , hdl : 1874/16625 , ISBN 978-3-540-52846-3.
Cattell, Kevin; Dinneen, Michael J .; Fellows, Michael R. (1996), "En enkel linjär tidsalgoritm för att hitta vägnedbrytning av liten bredd", Information Processing Letters , 57 (4): 197–203, arXiv : math / 9410211 , doi : 10.1016 / 0020 -0190 (95) 00190-5 , S2CID 2442557.
Coudert, David; Huc, Florian; Mazauric, Dorian (2012), "A distribuerad algoritm för beräkning av Node Söknummer i Trees" (PDF) , Algorithmica , 63 (1): 158-190, doi : 10,1007 / s00453-011-9524-3.
Coudert, David; Huc, Florian; Sereni, Jean-Sébastien (2007), "Pathwidth of outerplanar charts" (PDF) , Journal of Graph Theory , 55 (1): 27–41, doi : 10.1002 / jgt.20218.
Diestel, Reinhard (1995), "Graph Minors I: a short proof of the path-width theorem", Combinatorics, Probability and Computing , 4 (1): 27–30, doi : 10.1017 / S0963548300001450.
Diestel, Reinhard; Kühn, Daniela (2005), "Graph minor hierarchies", Discrete Applied Mathematics , 145 (2): 167–182, doi : 10.1016 / j.dam.2004.01.010.
Demaine, Erik D .; Hajiaghayi, MohammadTaghi ; Kawarabayashi, Ken-ichi (2005), "Algoritmisk graf mindre teori: nedbrytning, approximering och färgning", Proc. 46: e IEEE Symposium on Foundations of Computer Science (FOCS 2005) , s. 637–646, doi : 10.1109 / SFCS.2005.14 , ISBN 0-7695-2468-0, S2CID 13238254.
Downey, Rod G .; Fellows, Michael R. (1999), Parameterized Complexity , Springer-Verlag, ISBN 0-387-94883-X.
Dujmović, V .; Fellows, MR ; Kitching, M .; Liotta, G .; McCartin, C .; Nishimura, N .; Ragde, P .; Rosamond, F .; Whitesides, S .; Trä, David R. (2008), "På det parametriserade komplexitet skiktad grafritning", Algorithmica , 52 (2): 267-292, doi : 10,1007 / s00453-007-9151-1 , S2CID 2.298.634.
Dujmović, Vida ; Morin, Pat ; Wood, David R. (2003), "Banbredd och tredimensionella rätlinjiga ritningar av grafer" (PDF) , Proc. 10: e internationella symposiet om grafritning (GD 2002) , föreläsningsanteckningar inom datavetenskap, 2528 , Springer-Verlag, s. 42–53.
Ellis, JA; Sudborough, IH; Turner, JS (1983), "Grafavgränsning och söknummer", Proc. 1983 Allerton Conf. om kommunikation, kontroll och databehandling. Som citerats av Monien & Sudborough (1988) .
Ellis, JA; Sudborough, IH; Turner, JS (1994), "The vertex separation and search number of a tree", Information and Computation , 113 (1): 50–79, doi : 10.1006 / inco.1994.1064.
Feige, Uriel ; Hajiaghayi, Mohammadtaghi ; Lee, James R. (2005), "Improved approximation algorithms for minimum-weight vertex separators", Proc. 37: e ACM Symposium on Theory of Computing (STOC 2005) , s. 563–572, doi : 10.1145 / 1060590.1060674 , ISBN 1581139608, S2CID 14097859.
Fellows, Michael R .; Langston, Michael A. (1989), "On search decision and the efficiency of polynomial-time algorithms", Proc. 21st ACM Symposium on Theory of Computing , s. 501–512, doi : 10.1145 / 73007.73055 , ISBN 0897913078, S2CID 1854173.
Ferreira, Afonso G .; Song, Siang W. (1992), "Att uppnå optimalitet för gate-matrislayout och PLA-vikning: en grafteoretisk strategi", Proc. 1: a latinamerikanska symposiet om teoretisk informatik (LATIN '92) , föreläsningsanteckningar inom datavetenskap, 583 , Springer-Verlag, s. 139–153, doi : 10.1007 / BFb0023825 , hdl : 10068/43314 , ISBN 3-540-55284-7.
de Fluiter, Babette (1997), Algorithms for Graphs of Small Treewidth (PDF) , Ph.D. avhandling, Utrecht University , ISBN 90-393-1528-0, arkiverad från originalet (PDF) 2011-07-24 , hämtad 2010-05-06.
Fomin, Fedor V. (2003), "Pathwidth of planar and line charts", Grafer och kombinatorik , 19 (1): 91–99, doi : 10.1007 / s00373-002-0490-z , S2CID 43123449.
Fomin, Fedor V .; Høie, Kjartan (2006), "Pathwidth of cubic charts and exact algorithms", Information Processing Letters , 97 (5): 191–196, doi : 10.1016 / j.ipl.2005.10.012.
Fomin, Fedor V .; Kratsch, Dieter; Todinca, Ioan; Villanger, Yngve (2008), "Exakta algoritmer för trebredd och minimiutfyllning", SIAM Journal on Computing , 38 (3): 1058–1079, doi : 10.1137 / 050643350 , hdl : 1956/1151.
Fomin, Fedor V .; Thilikos, Dimitrios M. (2007), "On self duality of pathwidth in polyhedral graph embeddings", Journal of Graph Theory , 55 (1): 42-54, doi : 10.1002 / jgt.20219.
Garbe, Renate (1995), "Trädbredd och banbredd för jämförbarhetsdiagram över intervallbeställningar", Proc. 20th International Workshop Graph-Theoretic Concepts in Computer Science (WG'94) , Lecture Notes in Computer Science, 903 , Springer-Verlag, s. 26–37, doi : 10.1007 / 3-540-59071-4_35 , ISBN 978-3-540-59071-2.
Golovach, PA (1993), "Grafens skärbredd och linjediagrets vertexseparationsnummer ", Discrete Mathematics and Applications , 3 (5): 517-522, doi : 10.1515 / dma.1993.3.5.517 , S2CID 120745961.
Guha, Sudipto (2000), "Nestad graf dissektion och approximationsalgoritmer", Proc. 41. IEEE-symposiet om grunden för datavetenskap (FOCS 2000) , s. 126, doi : 10.1109 / SFCS.2000.892072 , ISBN 0-7695-0850-2, S2CID 9854056.
Gurski, Frank; Wanke, Egon (2007), "Linjediagram över avgränsad klickbredd", Diskret matematik , 307 (22): 2734-2754, doi : 10.1016 / j.disc.2007.01.020.
Gustedt, Jens (1993), "On the pathwidth of chordal charts", Discrete Applied Mathematics , 45 (3): 233–248, doi : 10.1016 / 0166-218X (93) 90012-D.
Habib, Michel; Möhring, Rolf H. (1994), "Trebredd för samfördelningsdiagram och en ny ordningsteoretisk parameter", Order , 11 (1): 47–60, doi : 10.1007 / BF01462229 , S2CID 2648030.
Hliněny, Petr (2003), "Crossing-number critical graphs have bounded path-width", Journal of Combinatorial Theory, Series B , 88 (2): 347–367, doi : 10.1016 / S0095-8956 (03) 00037-6.
Kashiwabara, T .; Fujisawa, T. (1979), "NP-fullständighet av problemet med att hitta ett intervalldiagram med minimiklicknummer som innehåller en given graf som en subgraf", Proc. Internationellt symposium om kretsar och system , s. 657–660.
Kinnersley, Nancy G. (1992), "Kodens separationsnummer för en graf är lika med dess banbredd", Information Processing Letters , 42 (6): 345–350, doi : 10.1016 / 0020-0190 (92) 90234-M.
Kinnersley, Nancy G .; Langston, Michael A. (1994), "Obstruktionsisolering för gate-matrislayoutproblemet", Diskret tillämpad matematik , 54 (2–3): 169–213, doi : 10.1016 / 0166-218X (94) 90021-3.
Kirousis, Lefteris M .; Papadimitriou, Christos H. (1985), "Intervalldiagram och sökning" (PDF) , Diskret matematik , 55 (2): 181–184, doi : 10.1016 / 0012-365X (85) 90046-9 , arkiverad från originalet ( PDF) den 2011-07-21.
Kloks, Ton; Bodlaender, Hans L. (1992), "Approximating treewidth and pathwidth of some classes of perfect charts", Proc. 3: e internationella symposiet om algoritmer och beräkning (ISAAC'92) , föreläsningsanteckningar inom datavetenskap, 650 , Springer-Verlag, s. 116–125, doi : 10.1007 / 3-540-56279-6_64 , hdl : 1874/16672 , ISBN 978-3-540-56279-5.
Kloks, T .; Bodlaender, H .; Müller, H .; Kratsch, D. (1993), "Computing treewidth and minimum fill-in: all you need is the minimal separators", Proc. 1: a europeiska symposiet om algoritmer (ESA'93) (Föreläsningsanteckningar inom datavetenskap) , 726 , Springer-Verlag, s. 260–271, doi : 10.1007 / 3-540-57273-2_61.
Kloks, Ton; Kratsch, Dieter; Müller, H. (1995), "Dominoes", Proc. 20: e internationella workshopen Grafteoretiska begrepp inom datavetenskap (WG'94) , föreläsningsanteckningar inom datavetenskap, 903 , Springer-Verlag, s. 106–120, doi : 10.1007 / 3-540-59071-4_41 , ISBN 978-3-540-59071-2.
Kneis, Joachim; Mölle, Daniel; Richter, Stefan; Rossmanith, Peter (2005), "Algoritmer baserade på träbredden för glesa grafer", Proc. 31: a internationella workshop om grafteoretiska begrepp inom datavetenskap (WG 2005) , föreläsningsanteckningar inom datavetenskap, 3787 , Springer-Verlag, s. 385–396, doi : 10.1007 / 11604686_34 , ISBN 978-3-540-31000-6.
Korach, Efraim; Solel, Nir (1993), "Trädbredd, stigbredd och skärbredd", Diskret tillämpad matematik , 43 (1): 97–101, doi : 10.1016 / 0166-218X (93) 90171-J.
Kornai, András; Tuza, Zsolt (1992), "Smalhet, vägbredd och deras tillämpning vid naturlig språkbehandling", Diskret tillämpad matematik , 36 (1): 87–92, doi : 10.1016 / 0166-218X (92) 90208-R.
Lengauer, Thomas (1981), "Svartvita småsten och grafavskiljning", Acta Informatica , 16 (4): 465–475, doi : 10.1007 / BF00264496 , S2CID 19415148.
Lopez, Alexander D .; Law, Hung-Fai S. (1980), "En tät grindmatrislayoutmetod för MOS VLSI", IEEE-transaktioner på elektronenheter , ED-27 (8): 1671–1675, Bibcode : 1980ITED ... 27.1671L , doi : 10.1109 / T-ED.1980.20086 , S2CID 64469353 , Även i den gemensamma utgåvan, IEEE Journal of Solid-State Circuits 15 (4): 736–740, 1980.
Miller, George A. (1956), "The Magical Number Seven, Plus or Minus Two" , Psychological Review , 63 (2): 81–97, doi : 10.1037 / h0043158 , hdl : 11858 / 00-001M-0000-002C -4646-B , PMID 13310704.
Möhring, Rolf H. (1990), "Grafproblem relaterade till grindmatrislayout och PLA-vikning", i Tinhofer, G .; Mayr, E .; Noltemeier, H .; et al. (red.), Computational Graph Theory , Computing Supplementum, 7 , Springer-Verlag, s. 17–51, ISBN 3-211-82177-5.
Monien, B .; Sudborough, IH (1988), "Min klippning är NP-komplett för kantviktade träd", Teoretisk datavetenskap , 58 (1–3): 209–229, doi : 10.1016 / 0304-3975 (88) 90028-X.
Ohtsuki, Tatsuo; Mori, Hajimu; Kuh, Ernest S .; Kashiwabara, Toshinobu; Fujisawa, Toshio (1979), "One-dimensional logic gate assignment and interval charts", IEEE Transactions on Circuits and Systems , 26 (9): 675–684, doi : 10.1109 / TCS.1979.1084695.
Peng, Sheng-Lung; Ho, Chin-Wen; Hsu, Tsan-sheng; Ko, Ming-Tat; Tang, Chuan Yi (1998), "En linjär tidsalgoritm för att konstruera en optimal nodsökningsstrategi för ett träd", Proc. 4: e Int. Konf. Computing and Combinatorics (COCOON'98) , Lecture Notes in Computer Science, 1449 , Springer-Verlag, s. 197–205.
Proskurowski, Andrzej; Telle, Jan Arne (1999), "Grafklasser med begränsade intervallmodeller" (PDF) , Diskret matematik och teoretisk datavetenskap , 3 : 167–176, arkiverad från originalet (PDF) 2011-06-06 , hämtad 2010 -05-06.
Robertson, Neil ; Seymour, Paul (1983), "Diagram mindreåriga. I. Exkluderar en skog", Journal of Combinatorial Theory, serie B , 35 (1): 39–61, doi : 10.1016 / 0095-8956 (83) 90079-5.
Robertson, Neil ; Seymour, Paul (2003), "Diagram minderåriga. XVI. Exkluderar en icke-plan graf", Journal of Combinatorial Theory, serie B , 89 (1): 43–76, doi : 10.1016 / S0095-8956 (03) 00042- X.
Robertson, Neil ; Seymour, Paul D. (2004), "Graph Minors. XX. Wagners antagande", Journal of Combinatorial Theory, serie B , 92 (2): 325–357, doi : 10.1016 / j.jctb.2004.08.001.
Scheffler, Petra (1990), "A linear algorithm for the pathwidth of trees", i Bodendiek, R .; Henn, R. (red.), Ämnen i kombinatorik och grafteori , Physica-Verlag, s. 613–620.
Scheffler, Petra (1992), "Optimal inbäddning av ett träd i ett intervalldiagram på linjär tid", i Nešetřil, Jaroslav ; Fiedler, Miroslav (red.), Fjärde tjeckoslovakiska symposiet om kombinatorik, diagram och komplexitet , Elsevier.
Skodinis, Konstantin (2000), "Beräkna optimala linjära layouter av träd i linjär tid", Proc. 8th European Symposium on Algorithms (ESA 2000) , Lecture Notes in Computer Science, 1879 , Springer-Verlag, s. 403–414, doi : 10.1007 / 3-540-45253-2_37 , ISBN 978-3-540-41004-1.
Skodinis, Konstantin (2003), "Konstruktion av linjära träd layouter som är optimala med avseende på vertex separation i linjär tid", Journal of Algorithms , 47 (1): 40-59, doi : 10,1016 / S0196-6774 (02) 00225-0.
Suchan, Karol; Todinca, Ioan (2007), "Pathwidth of circle-arc charts", Proc. 33: e internationella workshop om grafteoretiska begrepp inom datavetenskap (WG 2007) , föreläsningsanteckningar inom datavetenskap, 4769 , Springer-Verlag, s. 258–269, doi : 10.1007 / 978-3-540-74839-7_25.
Suderman, Matthew (2004), "Pathwidth and skiktade ritningar av träd" (PDF) , International Journal of Computational Geometry and Applications , 14 (3): 203–225, doi : 10.1142 / S0218195904001433 , arkiverad från originalet (PDF) på 2003-05-03.
Takahashi, Atsushi; Ueno, Shuichi; Kajitani, Yoji (1994), "Minsta acykliska förbjudna minderåriga för familjen av grafer med avgränsad vägbredd", Diskret matematik , 127 (1–3): 293–304, doi : 10.1016 / 0012-365X (94) 90092- 2.

Languages

In other projects