Cograph - Cograph

Den Turán graf T (13,4), ett exempel på en cograph

I grafteori , en cograph , eller komplement reducerbar graf , eller P ₄ -fri graf , är en graf som kan genereras från den enkelsträn vertex graf K ₁ genom komplemente och disjunkta unionen . Det vill säga, att familjen av cographs är den minsta klassen av grafer som inkluderar K ₁ och är stängd under komplettering och ojämn förening.

Grafer har upptäckts oberoende av flera författare sedan 1970-talet; tidiga referenser inkluderar Jung (1978) , Lerchs (1971) , Seinsche (1974) och Sumner (1974) . De har också kallats D * -grafer , ärftliga Dacey-grafer (efter det relaterade arbetet av James C. Dacey Jr. om ortomodulära gitter ) och 2-paritetsdiagram . De har en enkel strukturell sönderdelning med ojämn förening och kompletterar grafoperationer som kan representeras kortfattat av ett märkt träd, och används algoritmiskt för att effektivt lösa många problem, såsom att hitta den maximala klick som är svår för mer generella grafklasser.

Särskilda fall för graferna inkluderar kompletta grafer , kompletta tvåpartsdiagram , klusterdiagram och tröskeldiagram . Graferna är i sin tur speciella fall av avstånds-ärftliga grafer , permutationsdiagram , jämförbarhetsdiagram och perfekta grafer .

Definition

Rekursiv konstruktion

Vilken cograf som helst kan konstrueras enligt följande regler:

1. varje enskild vertexgraf är en graf;
2. om är en graf, så är dess komplementdiagram ;${\ displaystyle G}$ ${\ displaystyle {\ overline {G}}}$
3. om och är grafer, så är deras ojämna förening .${\ displaystyle G}$${\ displaystyle H}$${\ displaystyle G \ cup H}$

Graferna kan definieras som graferna som kan konstrueras med hjälp av dessa operationer, med utgångspunkt från kurvorna med en enda topp. Alternativt, istället för att använda komplementoperationen, kan man använda sammanfogningsoperationen, som består av att bilda den ojämna föreningen och sedan lägga till en kant mellan varje par av ett toppunkt från och ett toppunkt från . ${\ displaystyle G \ cup H}$${\ displaystyle G}$${\ displaystyle H}$

Andra karakteriseringar

Flera alternativa karakteriseringar av grafer kan ges. Bland dem:

• En cograph är en graf som inte innehåller den bana P ₄ på 4 vertex (och följaktligen av längd 3) som en inducerad subgraf . Det vill säga, en graf är en graf om och endast om det finns några hörn , om och är kanter av diagrammet, så är åtminstone en av eller också en kant.${\ displaystyle v_ {1}, v_ {2}, v_ {3}, v_ {4}}$${\ displaystyle \ {v_ {1}, v_ {2} \}, \ {v_ {2}, v_ {3} \}}$${\ displaystyle \ {v_ {3}, v_ {4} \}}$${\ displaystyle \ {v_ {1}, v_ {3} \}, \ {v_ {1}, v_ {4} \}}$${\ displaystyle \ {v_ {2}, v_ {4} \}}$
• En graf är en graf vars alla framkallade underbilder har den egenskapen att varje maximal klick skär varje maximal oberoende uppsättning i ett enda toppunkt.
• En graf är en graf i vilken varje icke-privat inducerad subgraf har minst två hörn med samma stadsdelar.
• En graf är en graf där varje ansluten inducerad subgraf har ett frånkopplat komplement.
• En graf är en graf vars alla anslutna inducerade underbilder har en diameter som högst 2.
• En graf är en graf där varje ansluten komponent är en avstånds-ärftlig graf med en diameter som högst 2.
• En cograph är ett diagram med klick-bredd som mest 2.
• En cograph är en jämförelse graf av en serie-parallell partiell ordning .
• En graf är ett permutationsdiagram för en separerbar permutation .
• En graf är en graf vars minimala ackorduppfyllelser är trivialt perfekta grafer .
• En graf är en ärftligt välfärgad graf , en graf så att varje girig färgning av varje inducerad subgraf använder ett optimalt antal färger.
• En graf är en cograph om och endast om varje vertex ordning grafen är en perfekt ordning , eftersom inte har någon P ₄ innebär att inga hinder för en perfekt ordning kommer att finnas i varje vertex ordning.

Cotrees

En cotree och motsvarande cograph. Varje kant ( u , v ) i grafen har en matchande färg till den minst gemensamma förfadern till u och v i cotree.

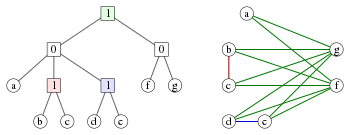
Ett cotree är ett träd i vilket de inre noderna är märkta med siffrorna 0 och 1. Varje cotree T definierar en graf G med bladen av T som hörn, och i vilken subtree rotad vid varje nod av T motsvarar den inducerade subgrafen i G definierad av uppsättningen blad som kommer ned från den noden:

• Ett underträd som består av en enda bladnod motsvarar en inducerad subgraf med ett enda toppunkt.
• Ett underträd rotat vid en nod märkt 0 motsvarar föreningen av underbilderna som definieras av barnen i den noden.
• Ett underträd rotat vid en nod märkt 1 motsvarar sammanfogningen av underbilderna som definieras av barnen i den noden; det vill säga vi bildar unionen och lägger till en kant mellan varannan hörn som motsvarar löv i olika underträd. Alternativt kan sammanfogningen av en uppsättning grafer ses som bildad genom att komplettera varje graf, bilda sammansättningen av komplementen och sedan komplettera den resulterande kopplingen.

Ett likvärdigt sätt att beskriva grafen som bildats av en cotree är att två hörn är förbundna med en kant om och endast om den lägsta gemensamma förfadern för motsvarande blad är märkt med 1. Omvänt kan varje cograph representeras på detta sätt av en cotree . Om vi ​​kräver att etiketterna på vilken som helst rotblad i detta träd växlar mellan 0 och 1, är denna representation unik.

Beräkningsegenskaper

Grafografier kan kännas igen linjärt och en cotree-representation konstrueras med hjälp av modulär sönderdelning , partitionsförfining , LexBFS eller delad sönderdelning . När en cotree-representation väl har konstruerats kan många bekanta grafproblem lösas via enkla bottom-up-beräkningar på cotrees.

Till exempel, för att hitta den maximala klicket i en graf, beräkna i botten-upp-ordning den maximala klicken i varje subgraf som representeras av ett underträd i cotree. För en nod märkt 0 är den maximala klicken det högsta bland de klick som beräknas för den nodens barn. För en nod märkt 1 är den maximala klicken föreningen av de klick som beräknas för den nodens barn och har storleken lika med summan av barnens klickstorlekar. Således, genom att växelvis maximera och summera värden lagrade vid varje nod i cotree, kan vi beräkna den maximala klickstorleken, och genom att växelvis maximera och ta fackföreningar, kan vi konstruera den maximala klicken själv. Liknande trädberäkningar från nedifrån och upp gör det möjligt att beräkna den maximala oberoende uppsättningen , vertexfärgningsantalet , maximalt klickomslag och Hamiltonicitet (det vill säga förekomsten av en Hamilton-cykel ) linjärt från en cotree-representation av en graf. Eftersom grafer har begränsat klickbredd kan Courcelles teorem användas för att testa alla egenskaper i monadisk andra ordningens grafiklogik (MSO ₁ ) på grafer i linjär tid.

Problemet med att testa huruvida ett visst diagram är k vertikalt bort och / eller t kanter bort från en graf är fast-parameter dragbar . Avgöra om en graf kan vara k -edge-utgår till en cograph kan lösas i O ^* (2,415 ^k ) tid, och k -edge-utformats en cograph i O ^* (4,612 ^k ). Om den största inducerade grafografiska undergrafen i en graf kan hittas genom att ta bort k- hörn från diagrammet, kan den hittas i O ^* (3.30 ^k ) tid.

Två grafer är isomorfa om och bara om deras cotrees (i kanonisk form utan två intilliggande hörn med samma etikett) är isomorfa. På grund av denna likvärdighet kan man i linjär tid avgöra om två grafer är isomorfa, genom att konstruera sina cotrees och tillämpa ett linjärt isomorfismtest för märkta träd.

Om H är en inducerad underbild av en graf G , är H i sig en graf; Cotree för H kan bildas genom att ta bort några av bladen från Cotree för G och sedan undertrycka noder som bara har ett barn. Det följer av Kruskals trädsättning att förhållandet att vara en inducerad subgraf är en väl kvasi-ordning på graferna. Således, om en underfamilj av tecknen (såsom de plana tecknen) stängs under inducerade subgrafoperationer, har den ett begränsat antal förbjudna inducerade underbilder . Beräkningsmässigt betyder detta att testa medlemskap i en sådan underfamilj kan utföras linjärt genom att använda en nedifrån och upp-beräkning på cotree i en given graf för att testa om den innehåller någon av dessa förbjudna underbilder. Men när storleken på två grafer är variabla är det NP-komplett att testa om den ena är en inducerad underbild av den andra .

Grafer spelar en nyckelroll i algoritmer för att känna igen läsfunktioner .

Uppräkning

Antalet anslutna grafer med n hörn, för n = 1, 2, 3, ..., är:

1, 1, 2, 5, 12, 33, 90, 261, 766, 2312, 7068, 21965, 68954, ... (sekvens A000669 i OEIS )

För n > 1 finns samma antal frånkopplade grafer, för exakt en av dem eller dess komplementdiagram är ansluten för varje graf .

Relaterade diagramfamiljer

Underklasser

Varje komplett graf K _n är en cograph, med en cotree bestående av en enda en-nod och n blad. På samma sätt varje komplett bipartit graf K _{a , b} är en cograph. Dess cotree är rotad i en 1-nod som har två 0-nod barn, en med en blad barn och en med b blad barn. En Turán-graf kan bildas genom sammanfogning av en familj av lika stora oberoende uppsättningar; sålunda är det också en cograf, med en cotree rotad vid en 1-nod som har en underlig 0-nod för varje oberoende uppsättning.

Varje tröskeldiagram är också en graf. En tröskeldiagram kan bildas genom att upprepade gånger lägga till ett toppunkt, antingen kopplat till alla tidigare vertikaler eller till ingen av dem; varje sådan operation är en av den ojämna fackföreningen eller gå med i operationer genom vilken en cotree kan bildas.

Superklasser

Karaktäriseringen av grafer med egenskapen att varje klick och maximal oberoende uppsättning har en icke-korsande skärningspunkt är en starkare version av den definierande egenskapen för starkt perfekta grafer , där varje inducerad subgraf innehåller en oberoende uppsättning som skär alla maximala klick. I en graf korsar varje maximal oberoende uppsättning alla maximala klick. Således är varje graf starkt perfekt.

Det faktum att cographs är P ₄ fri innebär att de är helt beställningsbar . I själva verket är varje toppordning av en graf en perfekt ordning som ytterligare innebär att maxklickfynd och minfärgning kan hittas i linjär tid med någon girig färgning och utan behov av en nedbrytning av cotree.

Varje graf är en avstånds-ärftlig graf , vilket betyder att varje inducerad väg i en graf är en kortaste väg . Graferna kan karakteriseras bland de avstånds-ärftliga graferna som att de har en diameter två i varje ansluten komponent. Varje graf är också ett jämförbarhetsdiagram för en serieparallell partiell ordning , erhållen genom att ersätta den ojämna facket och gå med i operationer genom vilka cografen konstruerades genom en oregelbunden förening och ordinarie summanoperationer på partiella beställningar. Eftersom starkt perfekta grafer, perfekt beställbara grafer, avstånds-ärftliga grafer och jämförelsegrafer är perfekta grafer , är grafer också perfekta.

Anteckningar

Referenser

externa länkar

• "Grafdiagram" , informationssystem om grafklassinkluderingar
• Weisstein, Eric W. "Cograph" . MathWorld .