Metoden för mekaniska satser -The Method of Mechanical Theorems

Metoden för mekaniska satser ( grekiska : Περὶ μηχανικῶν θεωρημάτων πρὸς Ἐρατοσθένη ἔφοδος ), även kallad The Method , anses vara ett av de stora överlevande verken av den antika grekiska polymat Archimedes . Metoden har formen av ett brev från Archimedes till Eratosthenes , huvudbibliotekarien vid biblioteket i Alexandria , och innehåller den första bevisade uttryckliga användningen av odelbara (ibland felaktigt kallade oändliga ). Arbetet trodde ursprungligen att vara förlorat, men 1906 återupptäcktes det i den berömda Archimedes Palimpsest . Palimpsest inkluderar Archimedes redogörelse för den "mekaniska metoden", så kallad eftersom den bygger på mitten av figurernas vikter ( centroid ) och spaken , som först demonstrerades av Archimedes i On the Equilibrium of Planes .

Arkimedes erkände inte metoden för odelbara som en del av rigorös matematik och publicerade därför inte hans metod i de formella avhandlingar som innehåller resultaten. I dessa avhandlingar bevisar han samma satser genom utmattning och hittar strikta övre och nedre gränser som båda överensstämmer med det svar som krävs. Ändå var den mekaniska metoden vad han använde för att upptäcka de relationer som han senare gav strikta bevis för.

Område av en parabel

För att förklara Archimedes metod idag är det bekvämt att använda lite kartesisk geometri, även om detta naturligtvis inte var tillgängligt vid den tiden. Hans idé är att använda hävstångens lag för att bestämma figurernas områden från den kända massan för andra figurer. Det enklaste exemplet i det moderna språket är parabolens område. Archimedes använder en mer elegant metod, men på kartesiskt språk beräknar hans metod integralen

{\ displaystyle \ int _ {0}^{1} x^{2} \, dx = {\ frac {1} {3}},}

som enkelt kan kontrolleras numera med hjälp av elementär integralkalkyl .

Tanken är att mekaniskt balansera parabolen (det krökta området som integreras ovan) med en viss triangel som är gjord av samma material. Parabolen är området i planet mellan -axeln och kurvan som varierar från 0 till 1. Triangeln är regionen i samma plan mellan -axeln och linjen , också som varierar från 0 till 1. ${\ displaystyle (x, y)}$ ${\ displaystyle x}$ ${\ displaystyle y = x^{2}}$ ${\ displaystyle x}$ ${\ displaystyle x}$ ${\ displaystyle y = x}$ ${\ displaystyle x}$

Skär parabolen och triangeln i vertikala skivor, en för varje värde av . Föreställ dig att -axeln är en spak, med en stödpunkt vid . Den lag av hävarmen anges att två föremål på motsatta sidor av hävstångsstödet kommer att balansera om vardera har samma vridmoment , där ett objekts vridmoment är lika med dess vikt gånger dess avstånd till stödpunkten. För varje värde av har skivan av triangeln i position en massa som är lika med dess höjd och ligger på ett avstånd från stödpunkten; så det skulle balansera motsvarande segment av parabolen, av höjd , om den senare flyttades till , på ett avstånd av 1 på andra sidan av stödpunkten. ${\ displaystyle x}$ ${\ displaystyle x}$ ${\ displaystyle x = 0}$ ${\ displaystyle x}$ ${\ displaystyle x}$ ${\ displaystyle x}$ ${\ displaystyle x}$ ${\ displaystyle x^{2}}$ ${\ displaystyle x = -1}$

Balanserad triangel och parabolisk spandrel med metoden

Eftersom varje par skivor balanserar, flyttar hela parabolen till skulle balansera hela triangeln. Det betyder att om den ursprungliga oklippta parabolen hängs upp av en krok från punkten (så att hela parabelns massa fästs vid den punkten), kommer den att balansera triangeln som sitter mellan och . ${\ displaystyle x = -1}$ ${\ displaystyle x = -1}$ ${\ displaystyle x = 0}$ ${\ displaystyle x = 1}$

Massans centrum för en triangel kan lätt hittas med följande metod, även på grund av Arkimedes. Om en medianlinje dras från någon av hörnen i en triangel till motsatt kant , kommer triangeln att balansera på medianen, betraktad som en stödpunkt. Orsaken är att om triangeln är uppdelad i oändliga ridsegment parallellt med , har varje segment lika lång längd på motsatta sidor av medianen, så balans följer med symmetri. Detta argument kan lätt göras rigoröst genom utmattning genom att använda små rektanglar istället för oändliga linjer, och detta är vad Archimedes gör i On the Equilibrium of Planes . ${\ displaystyle E}$ ${\ displaystyle E}$

Så massans centrum för en triangel måste vara vid skärningspunkten för medianerna. För triangeln i fråga är en median linjen , medan en andra median är linjen . När vi löser dessa ekvationer ser vi att skärningspunkten mellan dessa två medianer är över punkten , så att triangelns totala effekt på spaken är som om triangelns totala massa pressade ner på (eller hängde från) denna punkt. Det totala vridmomentet som triangeln utövar är dess area, 1/2, gånger avståndet 2/3 av dess masscentrum från stödpunkten vid . Detta vridmoment på 1/3 balanserar parabolen, som ligger på avstånd 1 från stödpunkten. Därför måste parabolens area vara 1/3 för att ge den motsatt vridmoment. ${\ displaystyle y = x/2}$ ${\ displaystyle y = 1-x}$ ${\ displaystyle x = 2/3}$ ${\ displaystyle x = 0}$

Denna typ av metod kan användas för att hitta området för en godtycklig sektion av en parabel, och liknande argument kan användas för att hitta integralen i vilken kraft som helst , även om högre makter blir komplicerade utan algebra. Arkimedes gick bara så långt som integralen av , som han använde för att hitta masscentrum för ett halvklot, och i annat arbete, masscentrum för en parabel. ${\ displaystyle x}$ ${\ displaystyle x^{3}}$

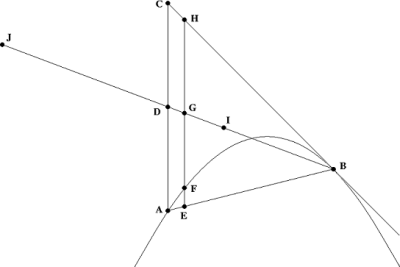
Första propositionen i palimpsest

Tänk på parabolen i figuren till höger. Välj två punkter på parabeln och kalla dem A och B .

Antag att linjesegmentet AC är parallellt med parabelns symmetriaxel. Vidare anta att de linjesegment BC ligger på en linje som är tangent till parabeln vid B . Det första förslaget säger:

Ytan på triangeln ABC är exakt tre gånger det område som avgränsas av parabolen och sekantlinjen AB .

Bevis :

Låt D vara mittpunkten för AC . Konstruera en linjesegment JB genom D , där avståndet från J till D är lika med avståndet från B till D . Vi kommer att tänka på segmentet JB som en "hävstång" med D som stödpunkt. Som Arkimedes tidigare visat är triangelns masscentrum vid punkten I på "spaken" där DI : DB = 1: 3. Därför är det tillräckligt att visa att om hela vikten av det inre av triangeln vilar på I , och hela vikten av delen av parabolen vid J , är spaken i jämvikt.

Tänk på ett oändligt litet tvärsnitt av triangeln som ges av segmentet HE , där punkten H ligger på BC , punkten E ligger på AB , och HE är parallell med parabelns symmetriaxel. Call korsningen av HE och parabeln F och skärningspunkten mellan HE och spaken G . Om hela triangelns vikt vilar på I , utövar den samma vridmoment på spaken JB som på HE . Således vill vi visa att om vikten av tvärsnittet HE vilar på G och vikten av tvärsnittet EF för parabolens sektion vilar på J , är spaken i jämvikt. Med andra ord räcker det med att visa att EF : GD = EH : JD . Men det är en rutinmässig följd av parabelns ekvation. QED

Sfärens volym

Återigen, för att belysa den mekaniska metoden är det bekvämt att använda lite koordinatgeometri. Om en sfär med radie 1 placeras med dess centrum vid x = 1, ges den vertikala tvärsnittsradien vid ett x mellan 0 och 2 med följande formel: ${\ displaystyle \ rho _ {S}}$

{\ displaystyle \ rho _ {S} (x) = {\ sqrt {x (2-x)}}.}

Massan av detta tvärsnitt, för balansering på en spak, är proportionell mot ytan:

{\ displaystyle \ pi \ rho _ {S} (x)^{2} = 2 \ pi x- \ pi x^{2}.}

Arkimedes övervägde sedan att rotera det triangulära området mellan y = 0 och y = x och x = 2 på x - y -planet runt x -axeln för att bilda en kon. Tvärsnittet av denna kon är en cirkel av radie ${\ displaystyle \ rho _ {C}}$

{\ displaystyle \ rho _ {C} (x) = x}

och området för detta tvärsnitt är

{\ displaystyle \ pi \ rho _ {C}^{2} = \ pi x^{2}.}

Så om skivor av konen och sfären båda ska vägas tillsammans, är den kombinerade tvärsnittsytan:

{\ displaystyle M (x) = 2 \ pi x.}

Om de två skivorna placeras ihop på avstånd 1 från stödpunkten, skulle deras totala vikt exakt balanseras av en områdescirkel på ett avstånd x från stödpunkten på andra sidan. Detta innebär att konen och sfären tillsammans, om allt material flyttades till x = 1 , skulle balansera en cylinder med basradie 1 och längd 2 på andra sidan. ${\ displaystyle 2 \ pi}$

Eftersom x sträcker sig från 0 till 2, kommer cylindern att ha ett tyngdpunkt på ett avstånd 1 från stödpunkten, så hela cylinderns vikt kan anses vara i position 1. Balansvillkoret säkerställer att konens volym plus sfärens volym är lika med cylinderns volym.

Cylinderns volym är tvärsnittsområdet, gånger höjden, som är 2, eller . Arkimedes kunde också hitta volymen av konen med hjälp av den mekaniska metoden, eftersom den integrerade delen i modern termer är exakt densamma som den för parabolens yta. Konens volym är 1/3 av dess basyta gånger höjden. Konens bas är en cirkel med radie 2, med area , medan höjden är 2, så är området . Att dra konens volym från cylinderns volym ger sfärens volym: ${\ displaystyle 2 \ pi}$ ${\ displaystyle 4 \ pi}$ ${\ displaystyle 4 \ pi}$ ${\ displaystyle 8 \ pi /3}$

{\ displaystyle V_ {S} = 4 \ pi -{8 \ over 3} \ pi = {4 \ over 3} \ pi.}

Beroendet av sfärens volym på radien är uppenbart från skalning, även om det inte heller var trivialt att göra strikt då. Metoden ger sedan den välkända formeln för volymen i en sfär . Genom att skala dimensionerna linjärt utvidgade Archimedes lätt volymresultatet till sfäroider .

Argimedes argument är nästan identiskt med argumentet ovan, men hans cylinder hade en större radie, så att konen och cylindern hängde på ett större avstånd från stödpunkten. Han ansåg att detta argument var hans största prestation och begärde att den medföljande figuren av den balanserade sfären, konen och cylindern skulle graveras på hans gravsten.

Ytan på en sfär

För att hitta sfärens ytarea argumenterade Archimedes att precis som cirkelns yta skulle kunna tänkas vara oändligt många oändliga högra trianglar som går runt omkretsen (se Cirkelmätning ), kunde sfärens volym tänkas på uppdelad i många kottar med höjd lika med radien och basen på ytan. Kottarna har alla samma höjd, så deras volym är 1/3 av basytan gånger höjden.

Arkimedes säger att sfärens totala volym är lika med volymen för en kon vars bas har samma ytarea som sfären och vars höjd är radien. Det finns inga detaljer för argumentet, men den uppenbara orsaken är att konen kan delas upp i oändliga kottar genom att dela upp basytan, och varje kon gör ett bidrag enligt sin basyta, precis som i sfären .

Låta ytan av sfären vara S . Volymen av kon med basen område S och höjden r är , vilket måste vara lika med volymen av sfären: . Därför måste sfärens ytarea vara , eller "fyra gånger dess största cirkel". Archimedes bevisar detta noggrant i On the Sphere and Cylinder . ${\ displaystyle Sr/3}$ ${\ displaystyle 4 \ pi r^{3}/3}$ ${\ displaystyle 4 \ pi r^{2}}$

Kurviga linjer med rationella volymer

En av de anmärkningsvärda sakerna med metoden är att Archimedes hittar två former definierade av sektioner av cylindrar, vars volym inte involverar , trots att formerna har kurvlinjära gränser. Detta är en central punkt i undersökningen - vissa kurvlinjära former kan korrigeras med linjal och kompass, så att det finns icke -rationella relationer mellan volymerna som definieras av skärningspunkten mellan geometriska fasta ämnen. ${\ displaystyle \ pi}$

Archimedes betonar detta i början av avhandlingen och uppmanar läsaren att försöka återge resultaten med någon annan metod. Till skillnad från de andra exemplen beräknas volymen av dessa former inte noggrant i något av hans andra verk. Av fragment i palimpsest verkar det som att Archimedes skrev in och omskrev former för att visa strikta gränser för volymen, även om detaljerna inte har bevarats.

De två formerna han anser är skärningspunkten mellan två cylindrar i rät vinkel ( bicylindern ), vilket är området för ( x , y , z ) att lyda:

{\ displaystyle x^{2}+y^{2} <1, \ quad y^{2}+z^{2} <1,}

och det cirkulära prisma, som är regionen som lyder:

{\ displaystyle x^{2}+y^{2} <1, \ quad 0 <z <y.}

Båda problemen har en skivning som ger en enkel integrering för den mekaniska metoden. För det cirkulära prisma, skär upp x -axeln i skivor. Området i y - z -planet vid vilket x som helst är det inre av en höger triangel med sidolängd vars yta är , så att den totala volymen är:

{\ displaystyle {\ sqrt {1-x^{2}}}}

{\ displaystyle {1 \ över 2} (1-x^{2})}

{\ displaystyle \ displaystyle \ int _ {-1}^{1} {1 \ över 2} (1-x^{2}) \, dx}

som enkelt kan åtgärdas med hjälp av den mekaniska metoden. Lägga till varje triangulär sektion en sektion av en triangulär pyramid med area balanserar ett prisma vars tvärsnitt är konstant.

{\ displaystyle x^{2}/2}

För skärningspunkten mellan två cylindrar går skivan förlorad i manuskriptet, men den kan rekonstrueras på ett självklart sätt parallellt med resten av dokumentet: om xz -planet är snittriktningen, ger ekvationerna för cylindern det samtidigt , som definierar ett område som är en kvadrat i x - z -planet med sidolängd , så att den totala volymen är: ${\ displaystyle x^{2} <1-y^{2}}$ ${\ displaystyle z^{2} <1-y^{2}}$ ${\ displaystyle 2 {\ sqrt {1-y^{2}}}}$

{\ displaystyle \ displaystyle \ int _ {-1}^{1} 4 (1-å^{2}) \, dy.}

Och detta är samma integral som för föregående exempel. Jan Hogendijk hävdar att förutom volymen på bicylindern kände Archimedes dess yta , vilket också är rationellt.

Andra propositioner i palimpsest

En rad geometriska propositioner bevisas i palimpsest av liknande argument. En sats är att placeringen av ett masscentrum i ett halvklot ligger 5/8 av vägen från polen till centrum av sfären. Detta problem är anmärkningsvärt, eftersom det utvärderar en kubisk integral.

Languages

In other projects