Median graf - Median graph

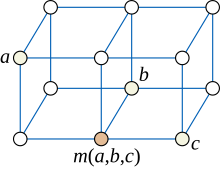
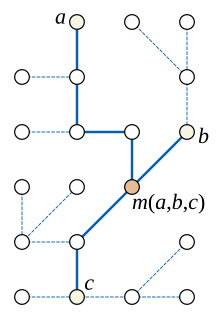
Medianen för tre hörn i en median graf

I grafteori , en division av matematiken , en median graf är en oriktad graf i vilken varje tre hörn en , b och c har en unik median : en vertex m ( a , b , c ) som tillhör kortaste vägar mellan varje par av a , b och c .

Begreppet mediangrafer har länge studerats, till exempel av Birkhoff & Kiss (1947) eller (mer uttryckligen) av Avann (1961) , men det första dokumentet som kallade dem "mediangrafer" verkar vara Nebeský (1971) . Som Chung , Graham och Saks skriver, "mediangrafer uppstår naturligt i studien av ordnade uppsättningar och diskreta distributiva galler , och har en omfattande litteratur". Inom fylogenetik är Buneman -grafen som representerar alla maximala parsimon evolutionära träd ett median diagram. Mediangrafer uppstår också i sociala valteorin : om en uppsättning alternativ har strukturen av en mediangraf, är det möjligt att på ett entydigt sätt härleda en majoritetspreferens bland dem.

Ytterligare undersökningar av mediangrafer ges av Klavžar & Mulder (1999) , Bandelt & Chepoi (2008) och Knuth (2008) .

Exempel

Medianen för tre hörn i ett träd, som visar delträdet som bildas genom föreningen av kortaste vägar mellan hörnen.

Varje träd är en median graf. För att se detta, observera att i ett träd är föreningen mellan de tre kortaste vägarna mellan paren i de tre hörnen a , b och c antingen själv en väg eller ett subtree som bildas av tre banor som möts vid en enda central nod med grad tre. Om föreningen mellan de tre vägarna själv är en väg, är medianen m ( a , b , c ) lika med en av a , b eller c , vilket av dessa tre hörn som är mellan de två andra i vägen. Om delträdet som bildas av föreningen mellan de tre vägarna inte är en väg, är medianen för de tre hörnen den centrala graden-tre-noden i delträdet.

Ytterligare exempel på mediangrafer tillhandahålls av rutdiagrammen . I ett rutdiagram kan koordinaterna för medianen m ( a , b , c ) hittas som medianen för koordinaterna för a , b och c . Omvänt visar det sig att man i varje mediangraf kan märka hörnen med punkter i ett heltalsgitter på ett sådant sätt att medianer kan beräknas koordinatmässigt på detta sätt.

En kvadrat .

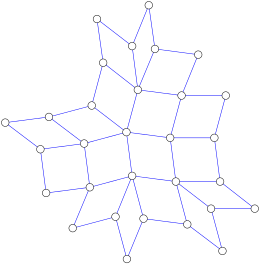
Kvadratgrafer , plana grafer där alla inre ytor är fyrkantiga och alla inre hörn har fyra eller flera infallande kanter, är en annan underklass av mediangraferna. En polyomino är ett specialfall av en kvadrat och bildar därför också en median graf.

Den simplex graf κ ( G ) hos en godtycklig oriktad graf G har ett vertex för varje klick (komplett delgraf) hos G ; två hörn av κ ( G ) är förenade genom en kant, om de motsvarande klickarna skiljer sig med en spets hos G . Simplexdiagrammet är alltid en mediangraf, där medianen för en given trippel av klickningar kan bildas genom att använda majoritetsregeln för att bestämma vilka hörn av klickarna som ska inkluderas.

Inga cykeldiagram med längre längd än fyra kan vara ett mediandiagram. Varje sådan cykel har tre hörn a , b och c så att de tre kortaste banorna sveper hela vägen runt cykeln utan att ha en gemensam korsning. För en sådan trippel av hörn kan det inte finnas någon median.

Motsvarande definitioner

I ett godtyckligt diagram, för varje två hörn a och b , kallas det minimala antalet kanter mellan dem deras avstånd , betecknat med d ( x , y ). Det intervall av hörn som ligger på kortaste vägar mellan en och b definieras som

I ( a , b ) = { v | d ( a , b ) = d (a, v) + d (v, b) }.

Ett mediandiagram definieras av egenskapen att för varje tre hörn a , b och c , skär dessa intervall i en enda punkt:

För alla a , b och c , | I ( a , b ) ∩ I ( a , c ) ∩ I ( b , c ) | = 1.

På motsvarande sätt kan man för varje tre hörn a , b och c hitta en toppunkt m ( a , b , c ) så att de ovägda avstånden i grafen uppfyller likheterna

d ( a , b ) = d ( a , m ( a , b , c )) + d ( m ( a , b , c ), b )
d ( a , c ) = d ( a , m ( a , b , c )) + d ( m ( a , b , c ), c )
d ( b , c ) = d ( b , m ( a , b , c )) + d ( m ( a , b , c ), c )

och m ( a , b , c ) är det enda hörnet för vilket detta är sant.

Det är också möjligt att definiera mediangrafer som lösningsuppsättningar för problem med 2-tillfredsställelse , som hyperkubernas indragningar , som graferna över ändliga medianalgebror , som Buneman-graferna för Helly-delade system och som graferna för windex 2; se avsnitten nedan.

Distributiva gitter och medianalgebror

Diagrammet över ett distributivt gitter, ritat som ett Hasse -diagram .

I gitterteorin har grafen för ett ändligt galler ett hörn för varje gitterelement och en kant för varje elementpar i täckförhållandet för gitteret. Gitter presenteras vanligen visuellt via Hasse -diagram , som är ritningar av grafer över galler. Dessa grafer, särskilt när det gäller distributiva gitter , visar sig vara nära besläktade med mediangrafer.

I ett distributivt gitter, Birkhoffs själv-dubbla ternära medianoperation

m ( a , b , c ) = ( a ∧ b ) ∨ ( a ∧ c ) ∨ ( b ∧ c ) = ( a ∨ b ) ∧ ( a ∨ c ) ∧ ( b ∨ c ),

uppfyller vissa nyckelaxiom, som den delar med den vanliga medianen av tal i intervallet från 0 till 1 och med medianalgebror mer allmänt:

Idempotens : m (a, a, b) = a för alla a och b .
Kommutativitet : m ( a , b , c ) = m (a, c, b) = m (b, a, c) = m (b, c, a) = m (c, a, b) = m (c , b, a) för alla a , b och c .
Distribution : m (a, m (b, c, d), e) = m (m (a, b, e), c, m (a, d, e)) för alla a , b , c , d , och e .
Identitetselement : m (0, a , 1) = a för alla a .

Den distributiva lagen kan ersättas av en associerad lag:

Associativitet : m ( x , w , m ( y , w , z )) = m ( m ( x , w , y ), w , z )

Medianoperationen kan också användas för att definiera en uppfattning om intervall för distributiva gitter:

I ( a , b ) = { x | m (a, x, b) = x } = { x | a ∧ b ≤ x ≤ a ∨ b }.

Diagrammet över ett ändligt distributivt gitter har en kant mellan hörnen a och b när jag ( a , b ) = { a , b }. För varje två hörn a och b i denna graf består intervallet I ( a , b ) definierat i gitterteoretiska termer ovan av hörnen på kortaste vägar från a till b , och sammanfaller således med de grafteoretiska intervall som definierats tidigare. För varje tre gitterelement är a , b och c , m ( a , b , c ) den unika skärningspunkten mellan de tre intervallen I ( a , b ), I ( a , c ) och I ( b , c ). Därför är diagrammet för ett godtyckligt ändligt distributivt gitter ett mediandiagram. Omvänt, om en median graf G innehåller två hörn 0 och 1 så att varannan toppunkt ligger på den kortaste vägen mellan de två (ekvivalent, m (0, a , 1) = a för alla a ), så kan vi definiera en distributiv galler där a ∧ b = m ( a , 0, b ) och a ∨ b = m ( a , 1, b ), och G kommer att vara grafen för detta gitter.

Duffus & Rival (1983) karakteriserar grafer över distributiva galler direkt som diametervarande inmatningar av hyperkubar. Mer allmänt ger varje mediangraf upphov till en ternär operation m som tillfredsställer idempotens, kommutativitet och distributivitet, men möjligen utan identitetselementen i ett distributivt gitter. Varje ternär operation på en ändlig uppsättning som uppfyller dessa tre egenskaper (men som inte nödvändigtvis har 0 och 1 element) ger på samma sätt upphov till en median graf.

Konvexa set och Helly -familjer

I en median graf, en uppsättning S är av vertex sägs vara konvex , om, för varje två hörn a och b tillhör S , hela intervallet I ( a , b är) en delmängd av S . Ekvivalent, med tanke på de två definitionerna av intervaller ovan, S är konvex om den innehåller varje kortaste vägen mellan två av dess hörn, eller om det innehåller medianen av varje uppsättning av tre punkter åtminstone två av dessa är från S . Observera att skärningspunkten mellan varje par konvexa uppsättningar i sig är konvex.

De konvexa uppsättningarna i en median graf har Helly-egenskapen : om F är en godtycklig familj av parvis korsande konvexa uppsättningar, så har alla uppsättningar i F en gemensam skärning. För om F bara har tre konvexa uppsättningar S , T och U i sig, med a i skärningspunkten mellan paret S och T , b i skärningspunkten mellan paret T och U , och c i skärningspunkten mellan paret S och U , då måste varje kortaste väg från a till b ligga inom T genom konvexitet, och på samma sätt måste varje kortaste väg mellan de två andra paren av hörn ligga inom de andra två uppsättningarna; men m ( a , b , c ) tillhör banor mellan alla tre hörnpar, så det ligger inom alla tre uppsättningarna och utgör en del av deras gemensamma skärningspunkt. Om F har mer än tre konvexa uppsättningar i det, följer resultatet genom induktion av antalet uppsättningar, för man kan ersätta ett godtyckligt par uppsättningar i F med deras skärningspunkt, med hjälp av resultatet för tripplar av uppsättningar för att visa att den ersatta familjen korsar fortfarande parvis.

En särskilt viktig familj av konvexa uppsättningar i ett mediandiagram, som spelar en roll som liknar halvrumsrum i det euklidiska rummet, är uppsättningarna

W _uv = { w | d ( w , u ) < d ( w , v )}

definieras för varje kant uv i grafen. Med ord består W _uv av hörnen närmare u än v , eller motsvarande hörnen w så att någon kortaste väg från v till w går genom u . För att visa att W _uv är konvext, låt w ₁w ₂ ... w _k vara en godtycklig kortaste väg som börjar och slutar inom W _uv ; då måste w ₂ också ligga inom W _uv , för annars kan de två punkterna m ₁ = m ( u , w ₁ , w _k ) och m ₂ = m ( m ₁ , w ₂ ... w _k ) visas (med med tanke på de möjliga avstånden mellan hörnen) för att vara distinkta medianer för u , w ₁ och w _k , vilket motsäger definitionen av en mediangraf som kräver att medianer är unika. Varje på varandra följande toppunkt på en kortaste väg mellan två hörn av W _uv ligger också inom W _uv , så W _uv innehåller alla kortaste vägar mellan dess noder, en av definitionerna av konvexitet.

Egenskapen Helly för uppsättningarna W _uv spelar en nyckelroll i karakteriseringen av mediangrafer som lösningen på 2-tillfredsställelseinstanser nedan.

2-tillfredsställelse

Mediangrafer har en nära koppling till lösningsuppsättningarna för problem med 2-tillfredsställelse som kan användas både för att karakterisera dessa grafer och för att relatera dem till kartor över hyperkubor som bevarar varandra.

En 2-tillfredsställelse-instans består av en samling booleska variabler och en samling klausuler , begränsningar för vissa variabelpar som kräver att dessa två variabler undviker vissa kombinationer av värden. Vanligtvis uttrycks sådana problem i konjunktiv normal form , där varje klausul uttrycks som en disjunktion och hela uppsättningen av begränsningar uttrycks som en konjunktion av klausuler, som t.ex.

{\ displaystyle (x_ {11} \ lor x_ {12}) \ land (x_ {21} \ lor x_ {22}) \ land \ cdots \ land (x_ {n1} \ lor x_ {n2}) \ land \ cdots.}

En lösning på en sådan instans är en tilldelning av sanningsvärden till de variabler som uppfyller alla klausuler, eller motsvarande som orsakar det konjunktiva normalformsuttrycket för instansen att bli sann när variabelvärdena ersätts med den. Familjen av alla lösningar har en naturlig struktur som en medianalgebra, där medianen av tre lösningar bildas genom att välja varje sanningvärde för att vara majoritetsfunktionen för värdena i de tre lösningarna; det är enkelt att verifiera att denna medianlösning inte kan bryta mot någon av klausulerna. Således bildar dessa lösningar en mediangraf, där granne till varje lösning bildas genom att negera en uppsättning variabler som alla är begränsade till att vara lika eller ojämlika med varandra.

Omvänt kan varje median graf G representeras på detta sätt som lösningen inställd på en 2-tillfredsställelse instans. För att hitta en sådan representation, skapa en 2-tillfredsställelse-instans där varje variabel beskriver orienteringen av en av kanterna i grafen (en tilldelning av en riktning till kanten som gör att grafen blir riktad snarare än oriktad) och varje begränsning tillåter två kanter för att dela ett par orienteringar endast när det finns en toppunkt v så att båda riktningarna ligger längs de kortaste banorna från andra hörn till v . Varje toppunkt v av G motsvarar en lösning på denna 2-tillfredsställelse-instans där alla kanter är riktade mot v . Varje lösning på instansen måste komma från någon toppunkt v på detta sätt, där v är den gemensamma skärningspunkten mellan uppsättningarna W _uw för kanter riktade från w till u ; denna gemensamma korsning existerar på grund av Helly -egenskapen för uppsättningarna W _uw . Därför överensstämmer lösningarna på denna 2-tillfredsställelse-instans en-mot-en med G- hörnen .

Returer av hyperkubar

Tillbakadragning av en kub på en sex-vertex subgraf.

En indragning av en graf G är en närliggande bevarande karta från G till en av dess undergrafer. Mer exakt är det grafhomomorfism φ från G till sig själv så att φ ( v ) = v för varje hörn v i subgrafen φ (G). Bilden av indragning kallas indragnings av G . Retraktioner är exempel på metriska kartor : avståndet mellan φ ( v ) och φ ( w ), för varje v och w , är högst lika med avståndet mellan v och w , och är lika när v och w båda tillhör φ ( G ). Därför måste en indragnings vara en isometrisk subgraf av G : avstånd i indragnings lika de i G .

Om G är en mediangraf, och a , b och c är en godtycklig tre hörn av en indragning φ ( G ), måste φ ( m ( a , b , c )) vara medianen av a , b och c , och så måste vara lika med m ( a , b , c ). Därför innehåller φ ( G ) medianer för alla tripplar av dess hörn och måste också vara en mediangraf. Med andra ord stängs familjen mediangrafer under indragningsoperationen.

En hyperkubgraf , där hörnen motsvarar alla möjliga k -bit bitvektorer och där två hörn ligger intill varandra när motsvarande bitvektorer skiljer sig åt endast i en enda bit, är ett specialfall för en k -dimensionell rutnätgraf och är därför en median Graf. Medianen för tre bitvektorer a , b och c kan beräknas genom att i varje bitposition beräkna majoritetsfunktionen för bitarna a , b och c . Eftersom mediangrafer stängs under indragning och inkluderar hyperkuberna, är varje indragning av en hyperkub ett mediandiagram.

Omvänt måste varje mediangraf vara en indragning av en hyperkub. Detta kan ses från sambandet, beskrivet ovan, mellan mediangrafer och 2-tillfredsställelse: låt G vara grafen över lösningar för en 2-tillfredsställelse-instans; utan förlust av generalitet kan denna instans formuleras på ett sådant sätt att inga två variabler alltid är lika eller alltid ojämlika i varje lösning. Då bildar utrymmet för alla sanningstilldelningar till variablerna i denna instans en hyperkub. För varje klausul, som bildas som en disjunktion av två variabler eller deras komplement, kan man i 2-tillfredsställelse-instansen bilda en återdragning av hyperkuben där sanningsuppgifter som bryter mot denna klausul mappas till sanningstilldelningar där båda variablerna uppfyller klausulen, utan att ändra de andra variablerna i sanningstilldelningen. Sammansättningen av indragningarna som bildas på detta sätt för var och en av klausulerna ger en indragning av hyperkuben till instansens lösningsutrymme och ger därför en representation av G som en hyperkubs indragning. I synnerhet är mediangrafer isometriska subgrafer av hyperkubar och är därför partiella kuber . Men inte alla partiella kuber är mediangrafer; till exempel är en sex-vertex cykeldiagram en partiell kub men är inte en median graf.

Som Imrich & Klavžar (2000) beskriver kan en isometrisk inbäddning av en mediangraf i en hyperkub konstrueras i tiden O ( m log n ), där n och m är antalet hörn respektive kanter på grafen.

Triangelfria grafer och igenkänningsalgoritmer

Konvertera en triangelfri graf till en median graf.

Problemen med att testa om en graf är en mediangraf och om en graf är triangelfri hade båda studerats väl när Imrich, Klavžar & Mulder (1999) observerade att de i någon mening är beräkningsekvivalenta. Därför gäller den mest kända tidsgränsen för att testa om en graf är triangelfri, O ( m ^1,41 ), liksom för att testa om en graf är en mediangraf, och eventuella förbättringar av mediangraftestalgoritmer skulle också leda till en förbättring i algoritmer för att detektera trianglar i grafer.

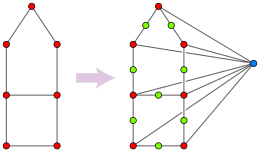
I en riktning, anta att en ges som inmatning av en graf G och måste testa om G är triangelfritt. Från G , konstruera en ny graf H , vilken som vertex varje uppsättning av noll, ett, eller två angränsande hörn av G . Två sådana uppsättningar ligger intill varandra i H när de skiljer sig åt med exakt en toppunkt. En ekvivalent beskrivning av H är att den bildas genom att dela varje kant av G till en stig av två kanter, och lägga till en ny toppunkt ansluten till alla de ursprungliga hörn av G . Denna graf H är genom konstruktion en partiell kub, men det är en mediangraf endast när G är triangelfritt: om a , b och c bildar en triangel i G , då { a , b }, { a , c }, och { b , c } har ingen medianen i H , för en sådan median skulle behöva motsvarar uppsättningen { a , b , c }, men uppsättningar av tre eller flera hörn i G inte bildar hörn i H . Därför är G triangelfritt om och bara om H är ett median diagram. Om G är triangelfritt är H dess simplexdiagram . En algoritm för att effektivt testa om H är ett median diagram kan med denna konstruktion också användas för att testa om G är triangelfritt. Denna omvandling bevarar beräkningskomplexiteten av problemet, för storleken på H är proportionell mot den för G .

Minskningen i den andra riktningen, från triangeldetektering till mediangrafprovning, är mer involverad och beror på den tidigare mediangrafigenkänningsalgoritmen för Hagauer, Imrich & Klavžar (1999) , som testar flera nödvändiga förutsättningar för mediangrafer i nära linjär tid . Det viktiga nya steget innebär att man använder en bredd första sökning för att dela upp grafens hörn i nivåer enligt deras avstånd från någon godtyckligt vald rotpunkt, bilda en graf från varje nivå där två hörn är intilliggande om de delar en gemensam granne i föregående nivå och söker efter trianglar i dessa grafer. Medianen för en sådan triangel måste vara en gemensam granne till de tre triangelns hörn; om denna gemensamma granne inte existerar är grafen inte ett mediandiagram. Om alla trianglar som finns på detta sätt har medianer, och den tidigare algoritmen finner att grafen uppfyller alla andra villkor för att vara en mediangraf, måste det faktiskt vara en mediangraf. Denna algoritm kräver inte bara möjligheten att testa om det finns en triangel, utan en lista över alla trianglar i nivådiagrammet. I godtyckliga grafer kräver listning av alla trianglar ibland Ω ( m ^3/2 ) tid, eftersom vissa grafer har så många trianglar, men Hagauer et al. visa att antalet trianglar som uppstår i nivågraferna för deras reduktion är nära linjärt, vilket gör att Alon et al. snabb matrismultiplikationsbaserad teknik för att hitta trianglar som ska användas.

Evolutionära träd, Buneman -grafer och Helly split -system

Buneman -grafen för fem typer av mus.

Fylogeni är slutsatsen av evolutionära träd från observerade egenskaper hos arter ; ett sådant träd måste placera arten på distinkta hörn och kan ha ytterligare latenta hörn , men de latenta hörnen måste ha tre eller flera infallande kanter och måste också märkas med egenskaper. En egenskap är binär när den bara har två möjliga värden, och en uppsättning arter och deras egenskaper uppvisar perfekt fylogeni när det finns ett evolutionärt träd där hörnen (arter och latenta hörn) märkta med något särskilt karakteristiskt värde bildar ett sammanhängande delträd. Om ett träd med perfekt fylogeni inte är möjligt, är det ofta önskvärt att hitta ett som uppvisar maximal parsimon , eller på motsvarande sätt, minimera antalet gånger ändpunkterna för en trädkant har olika värden för en av egenskaperna, summerade över alla kanter och alla egenskaper.

Buneman (1971) beskrev en metod för att utläsa perfekta fylogenier för binära egenskaper, när de finns. Hans metod generaliserar naturligtvis till konstruktionen av en mediangraf för alla typer av arter och binära egenskaper, som har kallats mediannätverket eller Buneman -grafen och är en typ av fylogenetiskt nätverk . Varje evolutionsträd för maximalt parsimonium inbäddat i Buneman -grafen, i den bemärkelsen att trädkanter följer banor i grafen och antalet karakteristiska värdeförändringar på trädkanten är samma som antalet i motsvarande sökväg. Buneman -grafen blir ett träd om och bara om det finns en perfekt fylogeni; detta händer när det inte finns två inkompatibla egenskaper för vilka alla fyra kombinationer av karakteristiska värden observeras.

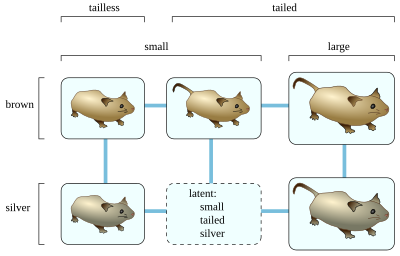
För att bilda Buneman -grafen för en uppsättning arter och egenskaper, eliminerar du först redundanta arter som inte går att skilja från vissa andra arter och redundanta egenskaper som alltid är desamma som någon annan egenskap. Därefter bildar du en latent toppunkt för varje kombination av karakteristiska värden så att varannan av värdena finns i några kända arter. I exemplet som visas finns det små bruna svansfria möss, små silverfria svansfria möss, små bruna svansmöss, stora bruna svansmöss och stora möss av silverhalv; Buneman -grafmetoden skulle bilda en latent toppunkt som motsvarar en okänd art av små silversvansade möss, eftersom varje parvis kombination (liten och silver, liten och stjärt och silver och stjärt) observeras hos några andra kända arter. Metoden skulle emellertid inte utgå från att det finns stora bruna svanslösa möss, eftersom det inte är känt att några möss har både de stora och de svanslösa egenskaperna. När de latenta hörnen har bestämts bildar du en kant mellan varje artpar eller latenta hörn som skiljer sig åt i en enda egenskap.

Man kan likvärdigt beskriva en samling av binära egenskaper som ett delat system , en familj av uppsättningar som har den egenskapen att komplementuppsättningen för varje uppsättning i familjen också är i familjen. Detta delade system har en uppsättning för varje karakteristiskt värde, bestående av de arter som har det värdet. När de latenta hörnen ingår har det resulterande delningssystemet Helly -egenskapen : varje parvis korsande underfamilj har en gemensam skärningspunkt. På något sätt kännetecknas mediangrafer som kommer från Helly split -system: paren ( W _uv , W _vu ) definierade för varje kant uv i en median graf bildar ett Helly split system, så om man tillämpar Buneman -grafkonstruktionen på detta system ingen latenta hörn kommer att behövas och resultatet blir detsamma som startdiagrammet.

Bandelt et al. (1995) och Bandelt, Macaulay & Richards (2000) beskriver tekniker för förenklad handberäkning av Buneman -grafen och använder denna konstruktion för att visualisera mänskliga genetiska samband.

Ytterligare fastigheter

Den kartesiska produkten av grafer bildar ett mediandiagram från två mindre mediangrafer.

Den kartesiska produkten av vartannat mediandiagram är en annan mediangraf. Medianer i produktdiagrammet kan beräknas genom att oberoende hitta medianerna i de två faktorerna, precis som medianer i rutdiagram kan beräknas genom att oberoende hitta medianen i varje linjär dimension.
Den windex av en graf mäter mängden av framåtblicks behövs för att optimalt lösa ett problem där en ges en sekvens av grafvertex s _i , och måste hitta som utmatning en annan sekvens av vertex t _jag minimera summan av avstånden $d (s i, t i)$ och $d (t i - 1, t i)$ . Mediangrafer är exakt de grafer som har windex 2. I en mediangraf är det optimala valet att ställa in $t i = m (t i - 1, s i, s i + 1)$ .
Egenskapen att ha en unik median kallas också den unika Steiner point -egenskapen . Ett optimalt Steiner -träd för tre hörn a , b och c i en median graf kan hittas som föreningen av tre kortaste vägar, från a , b och c till m ( a , b , c ). Bandelt & Barthélémy (1984) studerar mer allmänt problemet med att hitta toppunkten och minimera summan av avstånd till var och en av en uppsättning hörn, och visar att den har en unik lösning för alla udda antal hörn i en mediangraf. De visar också att denna medianen av en uppsättning S av hörn i en median graf tillfredsställer Condorcet kriteriet för vinnaren av ett val : jämfört med någon annan vertex, det är närmare en majoritet av hörnen i S .
Som med partiella kuber mer allmänt har varje mediangraf med n hörn högst ( n /2) log ₂ n kanter. Antalet kanter kan dock inte vara för litet: Klavžar, Mulder & Škrekovski (1998) bevisar att ojämlikheten $2 n - m - k \leq 2$ i varje mediangrafik håller, där m är antalet kanter och k är dimensionen av hyperkuben som grafen är en indragning av. Denna ojämlikhet är en jämlikhet om och bara om mediangrafen inte innehåller några kuber. Detta är en konsekvens av en annan identitet för mediangrafer: Euler-karaktäristiken Σ (-1) ^{dim ( Q )} är alltid lika med en, där summan tas över alla hyperkubunderdiagrammer Q i det angivna mediangrafen.
De enda vanliga mediangraferna är hyperkuberna.
Varje mediangraf är en modulär graf . De modulära graferna är en klass av grafer där varje trippel av hörn har en median men medianerna behöver inte vara unika.

Anteckningar

Referenser

Alon, Noga ; Yuster, Raphael; Zwick, Uri (1995), "Färgkodning", Journal of the ACM , 42 (4): 844–856, doi : 10.1145/210332.210337 , MR 1411787 , S2CID 208936467.
Avann, SP (1961), "Metric ternary distributive semi-gattices", Proceedings of the American Mathematical Society , 12 (3): 407–414, doi : 10.2307/2034206 , JSTOR 2034206 , MR 0125807.
Bandelt, Hans-Jürgen (1984), "Retracts of hypercubes", Journal of Graph Theory , 8 (4): 501–510, doi : 10.1002/jgt.3190080407 , MR 0766499.
Bandelt, Hans-Jürgen; Barthélémy, Jean-Pierre (1984), "Medianer i mediangrafer", Diskret tillämpad matematik , 8 (2): 131–142, doi : 10.1016/0166-218X (84) 90096-9 , MR 0743019.
Bandelt, Hans-Jürgen; Chepoi, Victor (2008), "Metric graph theory and geometry: a survey" (PDF) , Surveys on Discrete and Computational Geometry , Contemporary Mathematics, 453 , Providence, RI: American Mathematical Society, s. 49–86, doi : 10.1090 /conm/453/08795 , ISBN 9780821842393, MR 2405677.
Bandelt, Hans-Jürgen; Forster, P .; Sykes, BC; Richards, Martin B. (1 oktober 1995), "Mitokondriella porträtt av mänskliga populationer med mediana nätverk" , Genetics , 141 (2): 743–753, PMC 1206770 , PMID 8647407.
Bandelt, Hans-Jürgen; Forster, P .; Rohl, Arne (1 januari 1999), "Median-joining-nätverk för slutsatser om intraspecifika fylogenier" , Molecular Biology and Evolution , 16 (1): 37–48, doi : 10.1093/oxfordjournals.molbev.a026036 , PMID 10331250 , arkiverat från originalet den 27 december 2005.
Bandelt, Hans-Jürgen; Macaulay, Vincent; Richards, Martin B. (2000), "Median -nätverk: snabb konstruktion och girig minskning, en simulering och två fallstudier från human mtDNA", Molecular Phylogenetics and Evolution , 16 (1): 8–28, CiteSeerX 10.1.1.128. 3232 , doi : 10.1006/mpev.2000.0792 , PMID 10877936.
Barthélémy, Jean-Pierre (1989), "Från kopirhypergrafer till mediangrafer med latenta hörn", Diskret matematik , 76 (1): 9–28, doi : 10.1016/0012-365X (89) 90283-5 , MR 1002234.
Barthélemy, J.-P .; Leclerc, B .; Monjardet, B. (1986), "Om användningen av ordnade uppsättningar i jämförelseproblem och konsensus om klassificeringar", Journal of Classification , 3 (2): 187–224, doi : 10.1007/BF01894188 , S2CID 6092438.
Birkhoff, Garrett ; Kiss, SA (1947), "A ternary operation in distributive gitter" , Bulletin of the American Mathematical Society , 53 (1): 749–752, doi : 10.1090/S0002-9904-1947-08864-9 , MR 0021540.
Buneman, P. (1971), "Återhämtning av träd från mått på olikheter", i Hodson, FR; Kendall, DG; Tautu, PT (red.), Mathematics in the Archaeological and Historical Sciences , Edinburgh University Press, s. 387–395.
Chepoi, V .; Dragan, F .; Vaxès, Y. (2002), "Center- och diameterproblem vid plana fyrkantningar och trianguleringar", Proc. 13th ACM-SIAM Symposium on Discrete Algorithms , Soda '02, s. 346–355 , ISBN 9780898715132.
Chepoi, V .; Fanciullini, C .; Vaxès, Y. (2004), "Medianproblem i vissa plan trianguleringar och kvadranguleringar", Computational Geometry: Theory & Applications , 27 (3): 193–210, doi : 10.1016/j.comgeo.2003.11.002.
Chiba, N .; Nishizeki, T. (1985), "Arboricity and subgraph listing algoritms", SIAM Journal on Computing , 14 : 210–223, doi : 10.1137/0214017 , MR 0774940.
Chung, FRK ; Graham, RL ; Saks, ME (1987), "Dynamisk sökning i grafer", i Wilf, H. (red.), Diskreta algoritmer och komplexitet (Kyoto, 1986) (PDF) , Perspectives in Computing, 15 , New York: Academic Press, pp. 351–387, MR 0910939.
Chung, FRK ; Graham, RL ; Saks, ME (1989), "Ett dynamiskt platsproblem för grafer" (PDF) , Combinatorica , 9 (2): 111–132, doi : 10.1007/BF02124674 , S2CID 5419897.
Day, William HE; McMorris, FR (2003), Axiomatic Consensus Theory in Group Choice and Bioinformatics , Society for Industrial and Applied Mathematics, s. 91–94, ISBN 978-0-89871-551-4.
Klänning, A .; Hendy, M .; Huber, K .; Moulton, V. (1997), "Om antalet hörn och kanter på Buneman -grafen", Annals of Combinatorics , 1 (1): 329–337, doi : 10.1007/BF02558484 , MR 1630739 , S2CID 120716928.
Klänning, A .; Huber, K .; Moulton, V. (1997), "Några variationer på ett tema av Buneman", Annals of Combinatorics , 1 (1): 339–352, doi : 10.1007/BF02558485 , MR 1630743 , S2CID 122966547.
Duffus, Dwight ; Rival, Ivan (1983), "Graphs orientable as distributive gitter", Proceedings of the American Mathematical Society , 88 (2): 197–200, doi : 10.2307/2044697 , JSTOR 2044697.
Feder, T. (1995), Stabila nätverk och produktgrafer , Memoirs of the American Mathematical Society, 555.
Hagauer, Johann; Imrich, Wilfried; Klavžar, Sandi (1999), "Recognizing median graphs in subquadratic time", Theoretical Computer Science , 215 (1–2): 123–136, doi : 10.1016/S0304-3975 (97) 00136-9 , MR 1678773.
Hell, Pavol (1976), "Graph retractions", Colloquio Internazionale sulle Teorie Combinatorie (Roma, 1973), Tomo II , Atti dei Convegni Lincei, 17 , Rome: Accad. Naz. Lincei, s. 263–268, MR 0543779.
Imrich, Wilfried; Klavžar, Sandi (1998), "A convexity lemma and expansion procedures for bipartite graphs", European Journal of Combinatorics , 19 (6): 677–686, doi : 10.1006/eujc.1998.0229 , MR 1642702.
Imrich, Wilfried; Klavžar, Sandi (2000), Product Graphs: Structure and Recognition , Wiley, ISBN 978-0-471-37039-0, MR 0788124.
Imrich, Wilfried; Klavžar, Sandi; Mulder, Henry Martyn (1999), "Mediangrafer och triangelfria grafer", SIAM Journal on Discrete Mathematics , 12 (1): 111–118, CiteSeerX 10.1.1.28.5906 , doi : 10.1137/S0895480197323494 , MR 1666073.
Itai, A .; Rodeh, M. (1978), "Hitta en minimikrets i ett diagram", SIAM Journal on Computing , 7 (4): 413–423, doi : 10.1137/0207033 , MR 0508603.
Jha, Pranava K .; Slutzki, Giora (1992), "Konvexa expansionsalgoritmer för igenkänning och isometrisk inbäddning av mediangrafer", Ars Combinatoria , 34 : 75–92, MR 1206551.
Klavžar, Sandi; Mulder, Henry Martyn (1999), "Median grafer: characterizations, location theory and related structure" , Journal of Combinatorial Mathematics and Combinatorial Computing , 30 : 103–127, MR 1705337.
Klavžar, Sandi; Mulder, Henry Martyn; Škrekovski, Riste (1998), "En formel av Euler-typ för mediangrafer", Diskret matematik , 187 (1): 255–258, doi : 10.1016/S0012-365X (98) 00019-3 , MR 1630736.
Klavžar, Sandi; Škrekovski, Riste (2000), "On median graphs and median grid graphs", Discrete Mathematics , 219 (1–3): 287–293, doi : 10.1016/S0012-365X (00) 00085-6 , MR 1761732.
Knuth, Donald E. (2008), "Median algebras and median graphs", The Art of Computer Programming , IV, Fascicle 0: Introduction to Combinatorial Algorithms and Boolean Functions, Addison-Wesley, s. 64–74, ISBN 978-0-321-53496-5.
Mulder, Henry Martyn (1980), " $n$ -kuber och mediangrafer", Journal of Graph Theory , 4 (1): 107–110, doi : 10.1002/jgt.3190040112 , MR 0558458.
Mulder, Henry Martyn; Schrijver, Alexander (1979), "Median grafer and Helly hypergraphs" , Diskret matematik , 25 (1): 41–50, doi : 10.1016/0012-365X (79) 90151-1 , MR 0522746.
Nebeský, Ladislav (1971), "Median grafer", Commentationes Mathematicae Universitatis Carolinae , 12 : 317–325, MR 0286705.
Škrekovski, Riste (2001), "Två relationer för mediangrafer", Diskret matematik , 226 (1): 351–353, doi : 10.1016/S0012-365X (00) 00120-5 , MR 1802603.
Soltan, P .; Zambitskii, D .; Prisăcaru, C. (1973), extrema problem på grafer och algoritmer för deras lösning (på ryska), Chişinău: Ştiinţa.

externa länkar

Mediangrafer , informationssystem för grafklassinnehåll.
Nätverk , gratis fylogenetisk nätverksprogramvara. Nätverket genererar evolutionära träd och nätverk från genetiska, språkliga och andra data.
PhyloMurka , öppen källkodsprogramvara för mediana nätverksberäkningar från biologiska data.

Languages

In other projects