Kepler triangel -Kepler triangle

En Keplertriangel är en speciell rätvinklig triangel med kantlängder i geometrisk progression . Förhållandet mellan progressionen är var är det gyllene snittet , och progressionen kan skrivas: , eller ungefär . Kvadrater på kanterna av denna triangel har områden i en annan geometrisk progression, . Alternativa definitioner av samma triangel kännetecknar den i termer av de tre Pythagoras medel av två tal, eller via inradius av likbenta trianglar . ${\displaystyle {\sqrt {\varphi }}}$${\displaystyle \varphi =(1+{\sqrt {5}})/2}$${\displaystyle 1:{\sqrt {\varphi }}:\varphi }$${\displaystyle 1:1.272:1.618}$${\displaystyle 1:\varphi :\varphi ^{2}}$

Denna triangel är uppkallad efter Johannes Kepler , men kan hittas i tidigare källor. Även om vissa källor hävdar att forntida egyptiska pyramider hade proportioner baserade på en Kepler-triangel, tror de flesta forskare att det gyllene snittet inte var känt för egyptisk matematik och arkitektur.

Historia

Keplertriangeln är uppkallad efter den tyske matematikern och astronomen Johannes Kepler (1571–1630), som skrev om denna form i ett brev från 1597. Två begrepp som kan användas för att analysera denna triangel, Pythagoras sats och det gyllene snittet, var båda av intresse för Kepler, som han skrev någon annanstans:

Geometri har två stora skatter: den ena är Pythagoras sats, den andra uppdelningen av en linje i extrem och medeltal. Den första kan vi jämföra med en massa guld, den andra kan vi kalla en dyrbar juvel.

Kepler var dock inte den första som beskrev denna triangel. Kepler själv krediterade det till "en musikprofessor vid namn Magirus". Samma triangel förekommer tidigare i en bok om arabisk matematik , Liber mensurationum of Abû Bekr, känd från en 1100-talsöversättning av Gerard av Cremona till latin, och i Practica geometriae  [ it ] av Fibonacci (publicerad 1220–1221) , som definierade det på ett liknande sätt som Kepler. Lite tidigare än Kepler skrev Pedro Nunes om den 1567, och den har "sannolikt varit utbredd i senmedeltida och renässansmanuskripttraditioner". Den har också självständigt återupptäckts flera gånger, senare än Kepler.

Enligt vissa författare beskriver en gyllene pyramid med en fördubblad Kepler-triangel som sitt tvärsnitt exakt utformningen av egyptiska pyramider som den stora pyramiden i Giza ; en källa till denna teori är en felläsning av Herodotus från 1800-talet av pyramidologen John Taylor. Många andra teorier om proportioner har föreslagits för samma pyramid, utan samband med Keplertriangeln. Eftersom dessa olika teorier är väldigt lika i de numeriska värden de får, och på grund av felaktigheter i mätningen, delvis orsakade av förstörelsen av pyramidens yttre yta, är sådana teorier svåra att lösa baserat på rent fysiska bevis. Matchningen i proportioner till Kepler-triangeln kan mycket väl vara en numerisk slump: enligt forskare som har undersökt detta förhållande kände de forntida egyptierna med största sannolikhet inte till eller använde det gyllene snittet i sin matematik eller arkitektur. Istället kan pyramidens proportioner förklaras adekvat med hjälp av heltalsförhållanden, baserat på en rätvinklig triangel med sidorna 11 och 14.

Namnet "Keplertriangel" för denna form användes av Roger Herz-Fischler, baserat på Keplers brev från 1597, redan 1979. Ett annat namn för samma triangel, som användes av Matila Ghyka i sin bok från 1946 om det gyllene snittet, The Geometry of Art and Life , är "pristriangeln", efter pyramidologen WA Price.

Definitioner

Keplertriangeln är unikt definierad av egenskaperna att vara en rätvinklig triangel och att ha sina sidlängder i geometrisk progression, eller motsvarande ha kvadraterna på sina sidor i geometrisk progression. Förhållandet mellan sidolängdernas progression är , där är det gyllene snittet , och progressionen kan skrivas: , eller ungefär 1 : 1,272 : 1,618. Kvadrater på kanterna av denna triangel har områden i en annan geometrisk progression, . Att triangeln med dessa proportioner är en rätvinklig triangel följer av det faktum att, för kvadratiska kantlängder med dessa proportioner, det definierande polynomet för det gyllene snittet är detsamma som formeln som ges av Pythagoras sats för de kvadratiska kantlängderna av en rätvinklig triangel: ${\displaystyle {\sqrt {\varphi }}}$${\displaystyle \varphi =(1+{\sqrt {5}})/2}$${\displaystyle 1:{\sqrt {\varphi }}:\varphi }$${\displaystyle 1:\varphi :\varphi ^{2}}$

Eftersom denna ekvation är sann för det gyllene snittet, följer dessa tre längder Pythagoras sats och bildar en rätvinklig triangel. Omvänt, i varje rät triangel vars kvadratiska kantlängder är i geometrisk progression med något förhållande , antyder Pythagoras sats att detta förhållande lyder identiteten . Därför måste förhållandet vara den unika positiva lösningen till denna ekvation, det gyllene snittet, och triangeln måste vara en Kepler-triangel. ${\displaystyle \rho }$${\displaystyle \rho ^{2}=\rho +1}$

De tre kantlängderna och är det harmoniska medelvärdet , det geometriska medelvärdet och det aritmetiska medelvärdet av de två siffrorna . Dessa tre sätt att kombinera två tal studerades alla i den antika grekiska matematiken och kallas för pytagoreiska medel . Omvänt kan detta tas som en alternativ definition av Keplertriangeln: det är en rätvinklig triangel vars kantlängder är de tre pytagoreiska medelvärdena av några två tal. De enda trianglarna för vilka detta är sant är Kepler-trianglarna. ${\displaystyle 1}$${\displaystyle {\sqrt {\varphi }}}$${\displaystyle \varphi }$${\displaystyle \varphi \pm 1}$

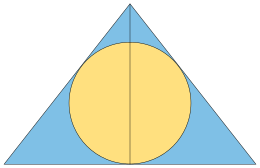
Ett tredje, ekvivalent sätt att definiera denna triangel kommer från ett problem med att maximera inradien av likbenta trianglar . Bland alla likbenta trianglar med ett fast val av längden på de två lika sidorna men med en variabel baslängd, är den med den största inradien bildad av två kopior av Keplertriangeln, reflekterade över deras kortaste kant från varandra. Därför kan Kepler-triangeln definieras som den räta triangeln som, bland alla räta trianglar med samma hypotenusa, med sin reflektion bildar den likbenta triangeln med maximal inradius. När Kepler-triangeln reflekteras på den längre av dess två vinkelräta sidor, bildar den istället den likbenta triangeln som, för en given omkrets, innehåller den största möjliga halvcirkeln .

Egenskaper

Om kortsidan av en Keplertriangel har längd , kommer de andra sidorna att ha längder och . Arean kan beräknas med standardformeln för arean av rätvinkliga trianglar (halva produkten av de två kortsidorna) som . Cosinus för den största av de två icke-räta vinklarna är förhållandet mellan den intilliggande sidan (den kortare av de två sidorna) och hypotenusan, , varav det följer att de två icke-räta vinklarna är ${\displaystyle s}$${\displaystyle s{\sqrt {\varphi }}}$${\displaystyle s\varphi }$${\displaystyle {\tfrac {s^{2}}{2}}{\sqrt {\varphi }}}$${\displaystyle \varphi }$

och

Jerzy Kocik har observerat att den största av dessa två vinklar också är den vinkel som bildas av centra för trippel av på varandra följande cirklar i Coxeters loxodromic sekvens av tangentcirklar .

Se även

• Automedian triangel , en triangel vars kvadratiska sidolängder bildar en aritmetisk progression, inklusive den räta triangeln med sidolängder${\displaystyle 1:{\sqrt {2}}:{\sqrt {3}}}$
• Gyllene triangel , en likbent triangel vars förhållande mellan bas och sidlängd är det gyllene snittet.

Referenser