Dominerande uppsättning - Dominating set

I grafteori , en dominerande uppsättning för en graf G  = ( V ,  E är) en delmängd D av V så att varje vertex inte i D är intill åtminstone en medlem av D . Den dominans nummer γ ( G ) är antalet hörn i den minsta dominerande uppsättning för  G .

Det dominerande uppsättningsproblemet gäller att testa om γ ( G ) ≤  K för en given graf G och ingång K ; det är ett klassiskt NP-komplett beslutsproblem i beräkningskomplexitetsteori . Det antas därför att det inte finns någon effektiv algoritm som hittar en minsta dominerande uppsättning för alla grafer, även om det finns effektiva approximationsalgoritmer, liksom både effektiva och exakta algoritmer för vissa grafklasser.

Figurerna (a) - (c) till höger visar tre exempel på dominerande uppsättningar för en graf. I varje exempel gränsar varje vit topp till åtminstone ett rött toppunkt, och det sägs att det vita toppunktet domineras av det röda toppunktet. Dominansnumret för denna graf är 2: exemplen (b) och (c) visar att det finns en dominerande uppsättning med två hörn, och det kan kontrolleras att det inte finns någon dominerande uppsättning med bara 1 toppunkt för denna graf.

Historia

Dominansproblemet studerades från 1950-talet och framåt, men graden av forskning om dominans ökade markant i mitten av 1970-talet. År 1972, Richard Karp bevisade inställda täck problem att vara NP-fullständigt . Detta hade omedelbara konsekvenser för det dominerande uppsättningsproblemet, eftersom det finns enkla toppar att sätta och kanta till icke-ojämn korsning mellan de två problemen. Detta visade att det dominerande uppsättningsproblemet också var NP-komplett .

Dominerande uppsättningar är av praktiskt intresse inom flera områden. I trådlöst nätverk används dominerande uppsättningar för att hitta effektiva rutter inom ad hoc-mobilnät. De har också använts i dokumentsammanfattning och vid utformning av säkra system för elnät.

Dominerande och oberoende uppsättningar

Dominerande uppsättningar är nära besläktade med oberoende uppsättningar : en oberoende uppsättning är också en dominerande uppsättning om och endast om det är en maximal oberoende uppsättning , så varje maximal oberoende uppsättning i en graf är nödvändigtvis också en minimal dominerande uppsättning.

Dominans av oberoende uppsättningar

En dominerande uppsättning kan eller inte vara en oberoende uppsättning. Till exempel visar figurerna (a) och (b) ovan oberoende dominerande uppsättningar, medan figur (c) illustrerar en dominerande uppsättning som inte är en oberoende uppsättning.

Det oberoende dominansnumret i ( G ) för en graf G är storleken på den minsta dominerande uppsättningen som är en oberoende uppsättning. På motsvarande sätt är det storleken på den minsta maximala oberoende uppsättningen. Ett minimum för i ( G ) övertas mindre element (endast de oberoende uppsättningar anses), så γ ( G ) ≤  i ( G ) för alla grafer G .

Ojämlikheten kan vara strikt - det finns diagram G för vilka γ ( G ) <  i ( G ). Låt till exempel G vara det dubbla stjärndiagrammet som består av hörn x ₁ , ..., x _p , a , b , y ₁ , ..., y _q , där p , q > 1. Kanterna på G definieras enligt följande: varje x _i ligger i anslutning till en , en ligger i anslutning till b , och b är intill varje b _j . Då är γ ( G ) = 2 eftersom { a , b } är en minsta dominerande uppsättning. Om p  ≤  q är i ( G ) = p + 1 eftersom { x ₁ , ..., x _p , b} är en minsta dominerande uppsättning som också är oberoende (det är en minsta maximala oberoende uppsättning).

Det finns diagramfamiljer där γ ( G ) =  i ( G ), det vill säga varje minsta maximala oberoende uppsättning är ett minimum dominerande uppsättning. Till exempel γ ( G ) =  i ( G ) om G är ett klofritt diagram .

En graf G kallas en dominans-perfekt graf om γ ( H ) =  i ( H ) i varje inducerad subgraf H av G . Eftersom en inducerad undergraf av ett klofritt diagram är klofritt följer det att varje klofria diagram också är dominans-perfekt.

För varje graf G är dess linjediagram L ( G ) klofri, och följaktligen är en minsta maximal oberoende uppsättning i L ( G ) också ett minimum dominerande uppsättning i L ( G ). En oberoende uppsättning i L ( G ) motsvarar en matchning i G , och en dominerande uppsättning i L ( G ) motsvarar en kant dominerar uppsättning i G . Därför har en minimal maximal matchning samma storlek som en minsta kantdominerande uppsättning.

Dominans av oberoende uppsättningar

Den oberoende dominans nummer iγ ( G ) hos en graf G är den maximala, över alla oberoende uppsättningar A av G , för den minsta uppsättningen dominerar A . Dominerar delmängder av vertex kräver potentiellt färre vertex än dominerar alla vertex, så iγ ( G ) ≤  y ( G ) för alla grafer G .

Ojämlikheten kan vara strikt - det finns diagram G för vilka γ ( G ) <  γ ( G ). Till exempel, för vissa heltal n , låt G vara ett diagram där hörnpunkterna är raderna och kolumnerna på ett n- by- n- kort, och två sådana hörn är anslutna om och bara om de skär varandra. De enda oberoende uppsättningarna är uppsättningar med endast rader eller uppsättningar med endast kolumner, och var och en av dem kan domineras av ett enda toppunkt (en kolumn eller en rad), så iγ ( G ) = 1. För att dominera alla hörn behöver vi dock minst en rad och en kolumn, så γ ( G ) = 2. Dessutom kan förhållandet mellan y ( G ) / iy ( G ) vara godtyckligt stort. Till exempel om hörnpunkterna i G är alla delmängder av kvadrater på ett n- by- n- kort, är fortfarande iγ ( G ) = 1, men γ ( G ) = n .

Den bi-oberoende dominans nummer iγi ( G ) hos en graf G är den maximala, över alla oberoende uppsättningar A av G , för den minsta oberoende uppsättning dominerar A . Följande förhållanden gäller för alla diagram G :

Algoritmer och beräkningskomplexitet

Problemet med set cover är ett välkänt NP-hårt problem - beslutsversionen av set cover var ett av Karps 21 NP-kompletta problem . Det finns ett par L-minskningar av polynomtid mellan det minsta dominerande uppsättningsproblemet och uppsättningsproblemet . Dessa minskningar ( se nedan ) visar att en effektiv algoritm för det minsta dominerande uppsättningsproblemet skulle ge en effektiv algoritm för uppsättningsproblemet och vice versa. Dessutom bevarar minskningarna approximationsförhållandet : för vilken som helst a, skulle en polynom-tid-a-approximationsalgoritm för minimala dominerande uppsättningar ge en polynom-a-approximationsalgoritm för uppsättningsomslagsproblemet och vice versa. Båda problemen är faktiskt Log-APX-kompletta .

Ungefärligheten för uppsättningen täcker också väl: en logaritmisk approximationsfaktor kan hittas med hjälp av en enkel girig algoritm och att hitta en sublogaritmisk approximationsfaktor är NP-hård. Mer specifikt ger den giriga algoritmen en faktor 1 + -logg | V | approximation av en minsta dominerande uppsättning och ingen polynom-tidsalgoritm kan uppnå en approximationsfaktor bättre än c  log | V | för vissa c  > 0 om inte P = NP .

L-minskningar

Följande två reduktioner visar att det minsta dominerande uppsättningsproblemet och uppsättningsproblemet är ekvivalenta under L-minskningar : givet en instans av ett problem kan vi konstruera en motsvarande instans av det andra problemet.

Från dominerande set till set cover. Givet ett diagram G  = ( V ,  E ) med V  = {1, 2, ...,  n }, konstruera en uppsättning täckningsinstans ( U ,  S ) enligt följande: universum U är V och familjen av underuppsättningar är S  = { S ₁ , S ₂ , ..., S _n } så att S _v består av vertex v och alla vertex intill v i G .

Om D nu är en dominerande uppsättning för G , är C  = { S _v  :  v  ∈  D } en möjlig lösning på problemet med uppsättning täckning, med | C | = | D |. Omvänt, om C  = { S _v  :  v  ∈  D } är en möjlig lösning på uppsättningen täckproblem, så är D en dominerande uppsättning för G , med | D | = | C |.

Därför är storleken på ett minsta dominerande set för G lika med storleken på ett minimum set cover för ( U ,  S ). Dessutom finns det en enkel algoritm som mappar en dominerande uppsättning till en uppsättning av samma storlek och vice versa. I synnerhet ger en effektiv a-approximationsalgoritm för uppsättningstäckning en effektiv a-approximationsalgoritm för minimala dominerande uppsättningar.

Till exempel, med tanke på diagrammet G som visas till höger, konstruerar vi en uppsättning täckningsinstans med universum U  = {1, 2, ..., 6} och delmängderna S ₁  = {1, 2, 5}, S ₂  = {1, 2, 3, 5}, S ₃  = {2, 3, 4, 6}, S ₄  = {3, 4}, S ₅  = {1, 2, 5, 6} och S ₆  = {3, 5, 6}. I det här exemplet är D  = {3, 5} en dominerande uppsättning för G - detta motsvarar uppsättningskåpan C  = { S ₃ ,  S ₅ }. Till exempel, vertex 4 ∈  V domineras av vertex 3 ∈  D , och elementet 4 ∈  U ingår i uppsättningen S ₃  ∈  C .

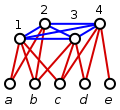
Från setskydd till dominerande set. Låt ( S ,  U ) vara en förekomst av uppsättningen täckproblem med universum U och familjen av underuppsättningar S  = { S _i  :  i  ∈  I }; vi antar att U och indexuppsättningen I är osammanhängande. Konstruera en graf G  = ( V ,  E ) enligt följande: uppsättningen av hörn är V  =  I  ∪  U , det finns en kant { i ,  j } ∈  E mellan varje par i ,  j  ∈  I , och det finns också en kant { i ,  u } för varje i  ∈  I och u  ∈  S _i . Det vill säga, G är en delad graf : I är en klick och U är en oberoende uppsättning .

Nu om C  = { S _i  :  i  ∈  D } är en möjlig lösning på uppsättningsproblemet för någon delmängd D  ⊆  I , är D en dominerande uppsättning för G , med | D | = | C |: För det första, för varje u  ∈  U finns ett i  ∈  D så att u  ∈  S _i , och genom konstruktion ligger u och i intill varandra i G ; därför domineras u av i . För det andra, eftersom D måste vara nonempty, varje i  ∈  I ligger i anslutning till ett hörn i D .

Omvänt, låt D vara en dominerande set för G . Då är det möjligt att konstruera en annan dominerande uppsättning X så att | X | ≤ | D | och X  ⊆  I : ersätt helt enkelt varje u  ∈  D  ∩  U med en granne i  ∈  I av u . Då är C  = { S _i  :  i  ∈  X } en möjlig lösning på uppsättningsproblemet med | C | = | X | ≤ | D |.

Illustrationen till höger visar konstruktionen för U  = { a ,  b ,  c ,  d ,  e }, I  = {1, 2, 3, 4}, S ₁  = { a ,  b ,  c }, S ₂  = { a ,  b }, S ₃  = { b ,  c ,  d } och S ₄  = { c ,  d ,  e }.

I det här exemplet är C  = { S ₁ ,  S ₄ } ett set cover; detta motsvarar den dominerande uppsättningen D  = {1, 4}.

D  = { a , 3, 4} är en annan dominerande uppsättning för grafen G . Givet D , kan vi konstruera en dominerande uppsättning X  = {1, 3, 4}, som inte är större än D , och som är en delmängd av I . Den dominerande uppsättningen X motsvarar uppsättningskåpan C  = { S ₁ ,  S ₃ ,  S ₄ }.

Speciella fall

Om diagrammet har maximal grad Δ, hittar den giriga approximationsalgoritmen en O (log Δ)-approximation av ett minimum dominerande set. Dessutom, låt d _g vara kardinaliteten för dominerande uppsättning erhålles med användning girig approximation därefter följande relation gäller, , där N är antalet noder och M är antalet kanter i given oriktad graf. För fast Δ kvalificerar detta sig som en dominerande uppsättning för APX- medlemskap; det är faktiskt APX-komplett. ${\ displaystyle d_ {g} \ leq N + 1 - {\ sqrt {2M + 1}}}$

Problemet medger ett polynom-time approximation schema (PTAS) för speciella fall som enhetsdiskdiagram och plana grafer . En minsta dominerande uppsättning finns i linjär tid i serie – parallella grafer .

Exakta algoritmer

En minsta dominerande uppsättning av ett n- vertikalt diagram kan hittas i tid O (2 ⁿ n ) genom att inspektera alla vertex-underuppsättningar. Fomin, Grandoni & Kratsch (2009) visar hur man hittar en minsta dominerande uppsättning i tid O (1,5137 ⁿ ) och exponentiellt utrymme, och i tid O (1,5264 ⁿ ) och polynomrum. En snabbare algoritm med användning av O (1.5048 ⁿ ) tid hittades av van Rooij, Nederlof & van Dijk (2009) , som också visar att antalet minsta dominerande uppsättningar kan beräknas under denna tid. Antalet minimala dominerande uppsättningar är högst 1.7159 ⁿ och alla sådana uppsättningar kan listas i tid O (1.7159 ⁿ ).

Parameteriserad komplexitet

Att hitta en dominerande uppsättning storlek k spelar en central roll i teorin om parametrerad komplexitet. Det är det mest kända problemet komplett för klass W [2] och används i många reduktioner för att visa intrång i andra problem. Speciellt är problemet inte fast-parameter som kan spåras i den meningen att ingen algoritm med körtid f ( k ) n ^{O (1)} för någon funktion f existerar såvida inte W-hierarkin kollapsar till FPT = W [2].

Å andra sidan, om ingångsdiagrammet är plant, förblir problemet NP-svårt, men en algoritm med fast parameter är känd. I själva verket har problemet en kärna med storlek linjär i k , och körtider som är exponentiella i √ k och kubik i n kan erhållas genom att tillämpa dynamisk programmering på en grennedbrytning av kärnan. Mer allmänt är det dominerande uppsättningsproblemet och många varianter av problemet fasta parametrar som kan parametreras när de parametreras av både storleken på den dominerande uppsättningen och storleken på den minsta förbjudna fullständiga tvåpartsundergrafiken ; det vill säga problemet är FPT på cykelfria grafer , en mycket allmän klass av glesa grafer som inkluderar de plana graferna.

Den kompletterande uppsättningen till en dominerande uppsättning, en icke-blockerare , kan hittas av en algoritm med fast parameter i valfri graf.

Varianter

En viktig underklass av de dominerande uppsättningarna är klassen av anslutna dominerande uppsättningar . Om S är en ansluten dominerande uppsättning kan man bilda ett spännande träd av G där S bildar uppsättningen av trädets icke-bladhörn; omvänt, om T är något som spänner över träd i en graf med mer än två hörn, så bildar de icke-bladhörnarna i T en ansluten dominerande uppsättning. Därför är att hitta minsta anslutna dominerande uppsättningar motsvarande att hitta spännande träd med maximalt antal blad.

En total dominerande uppsättning är en uppsättning hörn så att alla hörn i diagrammet (inklusive hörn i den dominerande uppsättningen själva) har en granne i den dominerande uppsättningen. Figur (c) ovan visar en dominerande uppsättning som är en ansluten dominerande uppsättning och en total dominerande uppsättning; exemplen i figurerna (a) och (b) är varken.

En k -tupeldominerande uppsättning är en uppsättning vertikaler så att varje toppunkt i diagrammet har åtminstone k grannar i uppsättningen. En (1 + log n) -tillnärmning av en minsta k -tuple-dominerande uppsättning kan hittas i polynomtid. På samma sätt är en k- dominerande uppsättning en uppsättning vertikaler så att varje toppunkt som inte finns i uppsättningen har åtminstone k grannar i uppsättningen. Medan varje diagram tillåter en k -dominerande uppsättning, är det bara grafer med minsta grad k  - 1 som tillåter en k -toppel dominerande uppsättning. Men även om grafen medger k-tupeldominerande uppsättning, kan en minsta k -toppledominerande uppsättning vara nästan k gånger så stor som en minsta k -dominerande uppsättning för samma graf; En (1,7 + log Δ)-approximation av en minsta k- dominerande uppsättning kan också hittas i polynomtid.

En stjärna-dominerar uppsättning är en delmängd D av V så att, för varje hörn v i V , den stjärn av v (uppsättningen av kanterna intill v ) skär stjärnan i vissa hörn i D . Det är uppenbart att om G har isolerade hörn har den inga stjärndominerande uppsättningar (eftersom stjärnan i isolerade hörn är tom). Om G inte har några isolerade hörn är varje dominerande uppsättning en stjärndominerande uppsättning och vice versa. Skillnaden mellan stjärndominans och vanlig dominans är större när deras fraktionerade varianter beaktas.

En domatisk partition är en partition av topparna i ojämna dominerande uppsättningar. Det domatiska antalet är den maximala storleken på en domatisk partition.

En evig dominerande uppsättning är en dynamisk version av dominans där en vertex v i dominerande uppsättning D väljs och ersätts med en granne u ( u är inte i D ) så att den modifierade D också är en dominerande uppsättning och denna process kan upprepas över alla oändliga sekvenser av val av hörn  v .

Se även

• Vizings antagande - relaterar dominansnumret för en kartesisk produkt av grafer till dominansnumret för dess faktorer.
• Ställ in täckproblem
• Bondage nummer

Anteckningar

Referenser

• Alber, Jochen; Fellows, Michael R ; Niedermeier, Rolf (2004), "Reduktion av polynomtid för dominerande uppsättning", Journal of the ACM , 51 (3): 363–384, arXiv : cs / 0207066 , doi : 10.1145 / 990308.990309 , S2CID  488501.
• Allan, Robert B .; Laskar, Renu (1978), "Om dominans och oberoende dominansnummer i en graf", Diskret matematik , 23 (2): 73–76, doi : 10.1016 / 0012-365X (78) 90105-X.
• Crescenzi, Pierluigi; Kann, Viggo; Halldórsson, Magnús; Karpinski, Marek ; Woeginger, Gerhard (2000), "Minimum dominating set", A Compendium of NP Optimization Problems.
• Dehne, Frank; Människor, Michael; Fernau, Henning; Prieto, Elena; Rosamond, Frances (2006), "Nonblocker: Parameterized algorithmics for minimum dominating set" (PDF) , SOFSEM 2006: 32nd Conference on Current Trends in Theory and Practice of Computer Science, Merin, Czech Republic, 21-27 januari, 2006, Proceedings , Lecture Notes in Computer Science, 3831 , Springer, s. 237–245, doi : 10.1007 / 11611257_21.
• Escoffier, Bruno; Paschos, Vangelis Th. (2006), "Fullständighet i ungefärliga klasser utöver APX", Teoretisk datavetenskap , 359 (1–3): 369–377, doi : 10.1016 / j.tcs.2006.05.023
• Faudree, Ralph ; Flandrin, Evelyne; Ryjáček, Zdeněk (1997), "Claw-free charts - A survey", Discrete Mathematics , 164 (1–3): 87–147, doi : 10.1016 / S0012-365X (96) 00045-3 , MR  1432221.
• Fomin, Fedor V .; Grandoni, Fabrizio; Kratsch, Dieter (2009), "A measure & conquer approach for the analysis of exact algorithms ", Journal of the ACM , 56 (5): 25: 1–32, doi : 10.1145 / 1552285.1552286 , S2CID  1186651.
• Fomin, Fedor V .; Grandoni, Fabrizio; Pyatkin, Artem; Stepanov, Alexey (2008), "Combinatorial bounds via measure and conquer: Bounding minimal dominating sets and applications", ACM Transactions on Algorithms , 5 (1): 9: 1–17, doi : 10.1145 / 1435375.1435384 , S2CID  2489447.
• Fomin, Fedor V .; Thilikos, Dimitrios M. (2006), "Dominerande uppsättningar i plana grafer: grenbredd och exponentiell hastighet", SIAM Journal on Computing , 36 (2): 281, doi : 10.1137 / S0097539702419649 , S2CID  5232238.
• Förster, Klaus-Tycho. (2013), "Approximating Fault-Tolerant Domination in General Graphs", Proc. i den tionde workshopen om analytisk algoritmik och kombinatorik ANALCO , SIAM, s. 25–32, doi : 10.1137 / 1.9781611973037.4 , ISBN 978-1-61197-254-2.
• Garey, Michael R .; Johnson, David S. (1979), Computers and Intractability: A Guide to theory of NP-Completeness , W. H. Freeman , ISBN 0-7167-1045-5, s. 190, problem GT2.
• Hedetniemi, ST; Laskar, RC (1990), "Bibliografi om dominans i grafer och några grundläggande definitioner av dominansparametrar", Diskret matematik , 86 (1–3): 257–277, doi : 10.1016 / 0012-365X (90) 90365-O.
• Kann, Viggo (1992), On the Approximability of NP-complete Optimization Problems (PDF) . Doktorsavhandling, Institutionen för numerisk analys och datavetenskap, Kungliga tekniska högskolan , StockholmCS1 maint: postscript ( länk ).
• Klasing, Ralf; Laforest, Christian (2004), "Hårdhetsresultat och approximationsalgoritmer för k-tupeldominering i grafer", Information Processing Letters , 89 (2): 75–83, doi : 10.1016 / j.ipl.2003.10.004.
• Papadimitriou, Christos H .; Yannakakis, Mihailis (1991), "Optimization, Approximation, and Complexity Classes", Journal of Computer and System Sciences , 43 (3): 425–440, doi : 10.1016 / 0022-0000 (91) 90023-X
• Parekh, Abhay K. (1991), "Analys av en girig heuristik för att hitta små dominerande uppsättningar i grafer", Information Processing Letters , 39 (5): 237–240, doi : 10.1016 / 0020-0190 (91) 90021-9
• Raz, R .; Safra, S. (1997), "Ett subkonstant fel-sannolikhet låggradigt test och subkonstant fel-sannolikhet PCP-karakterisering av NP", Proc. 29: e årliga ACM Symposium on Theory of Computing , ACM, s. 475–484, doi : 10.1145 / 258533.258641 , ISBN 0-89791-888-6, S2CID  15457604.
• Takamizawa, K .; Nishizeki, T .; Saito, N. (1982), "Linear-time computability of combinatorial problems on series – parallel charts", Journal of the ACM , 29 (3): 623–641, doi : 10.1145 / 322326.322328 , S2CID  16082154.
• Telle, Jan Arne; Villanger, Yngve (2012), "FPT-algoritmer för dominans i cykelfria grafer", i Epstein, Leah; Ferragina, Paolo (red.), Algoritmer - ESA 2012: 20: e årliga europeiska symposiet, Ljubljana, Slovenien, 10–12 september 2012, Proceedings , Lecture Notes in Computer Science , 7501 , Springer, s 802–812, doi : 10.1007 / 978-3-642-33090-2_69.
• van Rooij, JMM; Nederlof, J .; van Dijk, TC (2009), "Inklusion / uteslutning uppfyller mått och erövring: exakta algoritmer för att räkna dominerande uppsättningar", Proc. 17: e årliga europeiska symposiet om algoritmer, ESA 2009 , föreläsningsanteckningar i datavetenskap, 5757 , Springer, s. 554–565, doi : 10.1007 / 978-3-642-04128-0_50 , ISBN 978-3-642-04127-3.

Vidare läsning

• Grandoni, F. (2006), "A note on the complexity of minimum dominating set", Journal of Discrete Algorithms , 4 (2): 209–214, CiteSeerX  10.1.1.108.3223 , doi : 10.1016 / j.jda.2005.03 .002.
• Guha, S .; Khuller, S. (1998), "tillnärmning algoritmer för anslutna dominerande uppsättningar" (PDF) , Algorithmica , 20 (4): 374-387, doi : 10,1007 / PL00009201 , HDL : 1903/830 , S2CID  1.249.122.
• Haynes, Teresa W .; Hedetniemi, Stephen; Slater, Peter (1998a), Grundläggande dominans i grafer , Marcel Dekker, ISBN 0-8247-0033-3, OCLC  37903553.
• Haynes, Teresa W .; Hedetniemi, Stephen; Slater, Peter (1998b), Dominans i grafer: avancerade ämnen , Marcel Dekker, ISBN 0-8247-0034-1, OCLC  38201061.