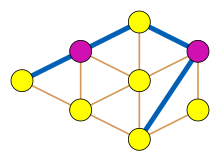
Klotfritt diagram - Claw-free graph

En klo

Inom grafteori , ett område av matematik, är en klofri graf en graf som inte har en klo som en inducerad subgraf .

En klo är ett annat namn för hela bipartitdiagrammet K 1,3 (det vill säga ett stjärndiagram med tre kanter, tre blad och en central toppunkt). En klofri graf är en graf där ingen inducerad subgraf är en klo; dvs varje delmängd av fyra hörn har andra än bara tre kanter som förbinder dem i detta mönster. På motsvarande sätt är en klofri graf en graf där grannskapet till någon toppunkt är komplementet till en triangelfri graf .

Klofria grafer studerades inledningsvis som en generalisering av linjediagram och fick ytterligare motivation genom tre viktiga upptäckter om dem: det faktum att alla klofria anslutna grafer av jämn ordning har perfekta matchningar , upptäckten av polynomiska tidsalgoritmer för att hitta maximal oberoende uppsättningar i klofria grafer och karakterisering av klofria perfekta grafer . De är föremål för hundratals matematiska forskningsartiklar och flera undersökningar.

Exempel

Den vanliga icosahedron, en polyhedron vars hörn och kanter bildar ett klofritt diagram.
  • Den linjediagrammet L ( G ) om varje graf G är klo-fri; L ( G ) har en spets för varje kant på G , och hörn är intill varandra i L ( G ) närhelst motsvarande kanter dela en slutpunkt i G . Ett linjediagram L ( G ) kan inte innehålla en klo, för om tre kanter e 1 , e 2 och e 3 i G alla delar slutpunkter med en annan kant e 4 så med duvhålsprincipen minst två av e 1 , e 2 , och e 3 måste dela en av dessa slutpunkter med varandra. Linjediagram kan karakteriseras i termer av nio förbjudna undergrafer; klo är den enklaste av dessa nio grafer. Denna karakterisering gav den första motivationen för att studera klofria grafer.
  • De Bruijn-graferna (grafer vars hörn representerar n -bit binära strängar för vissa n , och vars kanter representerar ( n-  1) -bit överlappningar mellan två strängar) är klofria. Ett sätt att visa detta är via konstruktionen av de Bruijn -grafen för n -bit -strängar som linjediagrammet för de Bruijn -grafen för ( n  -1) -bit -strängar.
  • Den komplementet av en triangel fria grafen är klo-free. Dessa grafer inkluderar som ett specialfall alla kompletta diagram .
  • Korrekta intervalldiagram , intervallgraferna som bildas som skärningsgrafer för intervallfamiljer där inget intervall innehåller ett annat intervall är klofria, eftersom fyra korrekt skärande intervall inte kan skäras i mönstret för en klo. Samma sak gäller i allmänhet för korrekta cirkelbågsdiagram .
  • Den Moser spindel , används en sju-vertex graf för att tillhandahålla en lägre gräns för den kromatiska antalet planet , är klo-fri.
  • Graferna för flera polyeder och polytoper är klofria, inklusive grafen för tetraedern och mer allmänt av varje simplex (en komplett graf), grafen för oktaedronen och mer allmänt av någon tvärpolytop ( isomorf till den cocktailpartygraf som bildas genom att ta bort en perfekt matchning från en komplett graf), grafen för den vanliga ikosahedronen och grafen för 16-cellen .
  • Den Schläfli grafen , ett starkt regelbunden kurva med 27 hörn, är klo-free.

Erkännande

Det är enkelt att verifiera att en given graf med n hörn och m kanter är klofri i tiden O ( n 4 ), genom att testa varje fyrfaldig hörn för att avgöra om de inducerar en klo. Med mer effektivitet och större komplikation kan man testa om en graf är klofri genom att för varje hörn av grafen kontrollera att komplementgrafen för sina grannar inte innehåller en triangel. En graf innehåller en triangel om och endast om kuben i dess angränsningsmatris innehåller ett icke -noll diagonalt element, så att hitta en triangel kan utföras under samma asymptotiska tidsbundna som n  ×  n matrismultiplikation . Därför skulle den totala tiden för denna klofria igenkänningsalgoritm vara O ( n 3.376 ) med hjälp av algoritmen Coppersmith – Winograd .

Kloks, Kratsch & Müller (2000) konstaterar att i varje klofritt diagram har varje hörn högst 2 √ m grannar; för annars skulle Turaks teorem inte ha grannarna till toppunktet tillräckligt med kvarvarande kanter för att utgöra komplementet till en triangelfri graf. Denna observation gör att kontrollen av varje grannskap i den snabbmatrismultiplikationsbaserade algoritmen som beskrivs ovan kan utföras under samma asymptotiska tidsgräns som 2 √ m  × 2 √ m matrismultiplikation, eller snabbare för hörn med ännu lägre grader. Det värsta fallet för denna algoritm inträffar när Ω ( √ m ) hörn har Ω ( √ m ) grannar var och de återstående hörnen har få grannar, så dess totala tid är O ( m 3,376/2 ) = O ( m 1,688 ).

Uppräkning

Eftersom klofria grafer inkluderar komplement till triangelfria grafer, växer antalet klofria grafer på n hörn minst lika snabbt som antalet triangelfria grafer, exponentiellt i kvadraten av n . Antalet anslutna klofria grafer på n noder, för n  = 1, 2, ... är

1, 1, 2, 5, 14, 50, 191, 881, 4494, 26389, 184749, ... (sekvens A022562 i OEIS ).

Om graferna tillåts kopplas bort är antalet grafer ännu större: de är

1, 2, 4, 10, 26, 85, 302, 1285, 6170, ... (sekvens A086991 i OEIS ).

En teknik från Palmer, Read & Robinson (2002) gör att antalet klorfria kubikdiagram kan räknas mycket effektivt, ovanligt för grafräkningsproblem .

Matchningar

Sumners bevis på att klofria anslutna grafer av jämn ordning har perfekta matchningar: att ta bort de två intilliggande hörnen v och w som är längst bort från u lämnar en ansluten subgraf, inom vilken samma borttagningsprocess kan upprepas.

Sumner (1974) och, oberoende av varandra, Las Vergnas (1975) bevisade att varje klofritt ansluten graf med ett jämnt antal hörn har en perfekt matchning . Det vill säga, det finns en uppsättning kanter i grafen så att varje hörnpunkt är en slutpunkt för exakt en av de matchade kanterna. Det speciella fallet med detta resultat för linjediagram innebär att man i alla diagram med ett jämnt antal kanter kan dela upp kanterna i banor med längd två. Perfekta matchningar kan användas för att ge en annan karakterisering av de klofria graferna: de är exakt de grafer där varje ansluten inducerad subgraf av jämn ordning har en perfekt matchning.

Sumners bevis visar, ännu starkare, att i alla anslutna klofria diagram kan man hitta ett par intilliggande hörn vars avlägsnande lämnar kvarvarande graf ansluten. För att visa detta hittar Sumner ett par hörn u och v som är så långt ifrån varandra som möjligt i grafen, och väljer w att vara en granne till v som är så långt från u som möjligt; som han visar kan varken v eller w ligga på någon kortaste väg från någon annan nod till u , så borttagandet av v och w lämnar kvarvarande graf ansluten. Att upprepade gånger ta bort matchade par hörn på detta sätt bildar en perfekt matchning i det givna klofria diagrammet.

Samma bevisidé gäller mer generellt om u är någon hörnpunkt, v är en hörnpunkt som är maximalt långt från u , och w är en granne till v som är maximalt långt från u . Avlägsnandet av v och w från grafen ändrar inte någon av de andra avstånden från u . Därför kan processen att bilda en matchning genom att hitta och ta bort par vw som är maximalt långt från u utföras av en enda postorderöverflyttning av ett första sökträd i grafen, rotat på u , i linjär tid. Chrobak, Naor & Novick (1989) tillhandahåller en alternativ linjär tidsalgoritm baserad på djup-första sökning , liksom effektiva parallella algoritmer för samma problem.

Faudree, Flandrin & Ryjáček (1997) listar flera relaterade resultat, inklusive följande: ( r  -1) -kopplade K 1, r -fria grafer av jämn ordning har perfekta matchningar för alla r  ≥ 2; klofria grafer av udda ordning med högst en grad-en toppunkt kan delas upp i en udda cykel och en matchning; för varje k som är högst hälften av miniminivån för en klofri graf där antingen k eller antalet hörn är jämnt har grafen en k -faktor; och, om en klofri graf är (2 k  + 1) ansluten, kan varje k- kantmatchning utökas till en perfekt matchning.

Oberoende uppsättningar

En icke-maximal oberoende uppsättning (de två violetta noder) och en förstärkningsväg

En oberoende uppsättning i ett linjediagram motsvarar en matchning i den underliggande grafen, en uppsättning kanter som inte två delar en slutpunkt. Den blomning algoritmen av Edmonds (1965) finner en maximal matchning i någon grafen i polynom tid, vilket är ekvivalent med beräkning av en maximal oberoende uppsättning i linjediagram. Detta har oberoende utvidgats till en algoritm för alla klofria grafer av Sbihi (1980) och Minty (1980) .

Båda tillvägagångssätten använder observationen att i klofria grafer kan ingen toppunkt ha mer än två grannar i en oberoende uppsättning, och därför måste den symmetriska skillnaden mellan två oberoende uppsättningar framkalla en subgraf av högst två; det vill säga det är en förening av vägar och cykler. I synnerhet, om jag är en icke-högsta oberoende uppsättning, skiljer den sig från varje maximal oberoende uppsättning med jämna cykler och så kallade förstärkningsvägar : inducerade vägar som växlar mellan hörn som inte är I och hörn i I , och för vilka båda slutpunkterna bara har en granne i jag . Eftersom den symmetriska skillnaden för I med någon förstärkningsväg ger en större oberoende uppsättning, reduceras uppgiften sålunda till att söka efter förstoringsvägar tills ingen mer kan hittas, analogt som i algoritmer för att hitta maximala matchningar.

Sbihis algoritm återskapar blomningskontraktionssteget i Edmonds algoritm och lägger till ett liknande, men mer komplicerat, klickkontraktionssteg . Mintys tillvägagångssätt är att omvandla probleminstansen till ett extra linjediagram och använda Edmonds algoritm direkt för att hitta förstoringsvägarna. Efter en korrigering av Nakamura & Tamura 2001 kan Mintys resultat också användas för att på polynomtid lösa det mer allmänna problemet med att hitta i klofria grafer en oberoende uppsättning av maximal vikt. Generaliseringar av dessa resultat till bredare klasser av grafer är också kända. Genom att visa en ny struktursats gav Faenza, Oriolo & Stauffer (2011) en kubisk tidsalgoritm, som också fungerar i den vägda inställningen.

Färgning, klick och dominans

En perfekt graf är en graf där det kromatiska talet och storleken på den maximala klicken är lika, och där denna jämlikhet kvarstår i varje inducerad subgraf. Det är nu känt (den starka perfekta grafsatsen ) att perfekta grafer kan karakteriseras som de grafer som inte har som inducerade subgrafer vare sig en udda cykel eller komplementet till en udda cykel (ett så kallat udda hål ). Men under många år förblev detta en olöst gissning, bara bevisad för speciella underklasser av grafer. En av dessa underklasser var familjen av klofria grafer: det upptäcktes av flera författare att klofria grafer utan udda cykler och udda hål är perfekta. Perfekta klofria grafer kan identifieras under polynomtid. I en perfekt klo-fri graf utgör grannskapet till någon toppunkt komplementet till en tvåpartig graf . Det är möjligt att färga perfekta klofria grafer, eller att hitta maximala klickningar i dem, på polynomtid.

Olöst problem i matematik :

Har klofria grafer alltid listkromatiska nummer lika med deras kromatiska nummer?

(fler olösta problem i matematik)

I allmänhet är det NP-svårt att hitta den största klicken i en klofri graf. Det är också NP-svårt att hitta en optimal färgning av grafen, eftersom (via linjediagram) detta problem generaliserar det NP-hårda problemet med att beräkna det kromatiska indexet för en graf. Av samma anledning är det svårt att hitta en färg som uppnår ett approximationsförhållande som är bättre än 4/3. Ett approximationsförhållande på två kan emellertid uppnås med en girig färgningsalgoritm , eftersom det kromatiska antalet hos en klöfri graf är större än hälften av dess maximala grad. En generalisering av kantlistans färgningskonstateri säger att listan kromatiskt tal är lika med det kromatiska talet för klofria grafer ; dessa två tal kan vara långt ifrån varandra i andra typer av grafer.

De klofria graferna är χ -gränsade , vilket innebär att varje klofritt diagram med stort kromatiskt tal innehåller en stor klick. Mer starkt följer det av Ramseys sats att varje klofritt diagram med stor högsta grad innehåller en stor klick, av storlek ungefär proportionell mot kvadratroten av graden. För anslutna klofria grafer som innehåller minst en oberoende uppsättning med tre vertex är ett starkare förhållande mellan kromatiskt tal och klickstorlek möjligt: ​​i dessa grafer finns det en klick av storlek minst hälften av det kromatiska talet.

Även om inte varje klorfri graf är perfekt, uppfyller klofria grafer en annan egenskap, relaterad till perfektion. En graf kallas dominans perfekt om den har en minsta dominerande uppsättning som är oberoende, och om samma egenskap innehar alla dess inducerade subgrafer. Klotfria grafer har denna egenskap. För att se detta, låt D vara en dominerande uppsättning i ett klofritt diagram, och anta att v och w är två intilliggande hörn i D ; då måste uppsättningen hörn som domineras av v men inte av w vara en klick (annars skulle v vara centrum för en klo). Om varje hörn i denna klick redan domineras av minst en annan medlem av D , kan v tas bort och producera en mindre oberoende dominerande uppsättning, och annars kan v ersättas av en av de odominerade hörnen i sin klick som producerar en dominerande uppsättning med färre adjacenser. Genom att upprepa denna ersättningsprocess når man så småningom en dominerande uppsättning som inte är större än D , så i synnerhet när startuppsättningen D är en minsta dominerande uppsättning bildar denna process en lika liten oberoende dominerande uppsättning.

Trots denna dominans perfektighet egenskap är det NP-svårt att bestämma storleken på den minsta dominerande uppsättningen i en klo-fri graf. I motsats till situationen för mer allmänna klasser av grafer, hitta den minsta dominerande set eller minimi anslutna dominerande som i en klo-free grafen är fast parameter lätthanterlig : det kan lösas i tid begränsas av en polynom i storlek i diagrammet multiplicerat med en exponentiell funktion av den dominerande uppsättningsstorleken.

Strukturera

Chudnovsky & Seymour (2005) översikt över en serie papper där de bevisar en strukturteori för klofria grafer, analogt med grafstruktursatsen för mindre stängda graffamiljer som bevisats av Robertson och Seymour, och med strukturteorin för perfekta grafer som Chudnovsky, Seymour och deras medförfattare använde för att bevisa den starka perfekta grafsatsen. Teorin är för komplex för att beskrivas i detalj här, men för att ge en smak av den räcker det med att beskriva två av deras resultat. För det första, för en speciell underklass med klofria grafer som de kallar kvasilinjediagram (ekvivalent, lokalt med tvåpartiga grafer), anger de att varje sådan graf har en av två former:

  1. Ett luddigt cirkulärt intervalldiagram , en klass av grafer som representeras geometriskt av punkter och bågar på en cirkel, vilket generaliserar korrekta cirkelbågsdiagram.
  2. En graf konstruerad från en multigraf genom att ersätta varje kant med en suddig linjär intervallgraf . Detta generaliserar konstruktionen av ett linjediagram, där varje kant av multigrafen ersätts av en toppunkt. Luddiga linjära intervalldiagram är konstruerade på samma sätt som luddiga cirkulära intervalldiagram, men på en linje snarare än på en cirkel.

Chudnovsky och Seymour klassificerar godtyckliga anslutna klofria grafer till något av följande:

  1. Sex specifika underklasser av klofria grafer. Tre av dessa är linjediagram, korrekta cirkelbågsdiagram och de inducerade subgraferna av en ikosaeder; de andra tre innebär ytterligare definitioner.
  2. Grafer som bildas på fyra enkla sätt utifrån mindre klofria grafer.
  3. Antiprismatiska grafer , en klass med täta grafer som definieras som de klofria graferna där var fjärde hörn inducerar en subgraf med minst två kanter.

Mycket av arbetet i deras strukturteori innebär en ytterligare analys av antiprismatiska grafer. Den Schläfli grafen , en klo-free starkt regelbunden diagram med parametrar SRG (27,16,10,8), spelar en viktig roll i denna del av analysen. Denna strukturteori har lett till nya framsteg inom polyhedral kombinatorik och nya gränser för det kromatiska antalet klofria grafer, liksom nya fasta parametrar som kan behandlas för att dominera uppsättningar i klofria grafer.

Anteckningar

Referenser

externa länkar