Räkningsbart set - Countable set

"Räkningsbara" omdirigeringar här. För det språkliga begreppet, se Count substantiv . För det politiska medieföretaget, se Countable (app) .
För att inte förväxla med (rekursivt) otaliga uppsättningar .

I matematik är en räknarbar uppsättning en uppsättning med samma kardinalitet ( antal element) som någon delmängd av uppsättningen naturliga tal . En räkningsbar uppsättning är antingen en begränsad uppsättning eller en oändligt stor mängd. Vare sig det är ändligt eller oändligt, elementen i en räknarbar uppsättning kan alltid räknas en i taget och - även om räkningen kanske aldrig avslutas - är varje element i uppsättningen associerat med ett unikt naturligt tal.

Georg Cantor introducerade konceptet med räknbara uppsättningar, kontrasterande uppsättningar som kan räknas med de som inte kan räknas . Idag utgör räknarbara uppsättningar grunden för en gren av matematiken som kallas diskret matematik .

En anteckning om terminologi

Även om termerna "räknar" och "oändligt oändligt" som definieras här är ganska vanliga, är terminologin inte universell. En alternativ stil använder räkningsbart för att betyda det som här kallas för oändligt, och högst för att räkna med det som här kallas för räknarbart. För att undvika tvetydighet kan man begränsa sig till termerna "högst räknade" och "oändligt oändligt", men med avseende på koncision är detta det värsta av båda världarna. Läsaren uppmanas att kontrollera definitionen som används när man stöter på termen "räknas" i litteraturen.

Termerna uppräkningsbara och uppräkningsbara kan också användas, t.ex. hänvisa till räknbara respektive oändligt många, men när definitionerna varierar rekommenderas läsaren återigen att kontrollera definitionen som används.

Definition

Den mest kortfattade definitionen är när det gäller kardinalitet . En uppsättning S är uppräknelig om dess kardinalitet | S | är mindre än eller lika med ( aleph-noll ), kardinaliteten av uppsättningen av naturliga tal N . En uppsättning S är uppräkneligt oändlig om | S | = . En uppsättning kan inte räknas om den inte kan räknas, dvs dess kardinalitet är större än ; läsaren hänvisas till Uncountable set för vidare diskussion.

På motsvarande sätt kan en uppsättning S räknas iff :

  • det existerar en injektiv funktion från S till N .
  • S är tomt eller det finns en surjektiv funktion från N till S , eller.
  • det existerar en bijektiv avbildning mellan S och en delmängd av N .
  • S är antingen ändligt eller oändligt oändligt.

På samma sätt är en uppsättning S oändligt oändlig iff :

  • det finns en injektiv och surjektiv (och därför bijektiv ) mappning mellan S och N . Med andra ord, är en uppsättning uppräkneligt oändlig om den har ett-till-ett korrespondens med den naturliga antal set, N .
  • Elementen i S kan ordnas i en oändlig sekvens , där det skiljer sig från för och varje element i S listas.

Historia

År 1874, i sin första uppsättningsteorikartikel , visade Cantor att mängden av verkliga tal är otaliga, vilket visar att inte alla oändliga uppsättningar kan räknas. År 1878 använde han en-till-en-korrespondenser för att definiera och jämföra kardinaliteter. År 1883 utökade han de naturliga siffrorna med sina oändliga ordinaler och använde uppsättningar av ordinarier för att producera en oändlighet av uppsättningar med olika oändliga kardinaliteter.

Introduktion

En uppsättning är en samling element och kan beskrivas på många sätt. Ett sätt är helt enkelt att lista alla dess element; till exempel kan uppsättningen som består av heltal 3, 4 och 5 betecknas {3, 4, 5}, kallad rosterform. Detta är dock endast effektivt för små uppsättningar; för större uppsättningar skulle detta vara tidskrävande och felaktigt. Istället för att lista varje enskilt element används ibland en ellips ("...") för att representera många element mellan startelementet och slutelementet i en uppsättning, om författaren tror att läsaren enkelt kan gissa vad ... representerar ; till exempel {1, 2, 3, ..., 100} betecknar antagligen uppsättningen heltal från 1 till 100. Även i det här fallet är det dock fortfarande möjligt att lista alla element, eftersom antalet element i uppsättningen är ändlig.

Vissa uppsättningar är oändliga ; dessa uppsättningar har mer än n element där n är ett heltal som kan specificeras. (Oavsett hur stort det angivna heltalet n är, till exempel n = 9 × 10 32 , har oändliga uppsättningar fler än n element.) Till exempel uppsättningen naturliga tal, som kan anges med {0, 1, 2, 3, 4 , 5, ...}, har oändligt många element, och vi kan inte använda något naturligt tal för att ange dess storlek. Ändå visar det sig att oändliga uppsättningar har en väldefinierad uppfattning om storlek (eller mer korrekt, kardinalitet , den tekniska termen för antalet element i en uppsättning), och inte alla oändliga uppsättningar har samma kardinalitet.

Bijektiv mappning från heltal till jämna tal

För att förstå vad detta betyder undersöker vi först vad det inte betyder. Till exempel finns det oändligt många udda heltal, oändligt många jämna heltal och (därmed) oändligt många heltal totalt. Det visar sig dock att antalet jämna heltal, som är samma som antalet udda heltal, också är samma som antalet heltal totalt. Detta beror på att vi kan ordna saker så att det för varje heltal finns ett distinkt jämnt heltal:

eller, mer allmänt, (se bild). Vad vi har gjort här är att ordna heltal och jämna heltal i en en-till-en-korrespondens (eller bijektion ), vilket är en funktion som kartlägger mellan två uppsättningar så att varje element i varje uppsättning motsvarar ett enda element i den andra uppsättning.

Men inte alla oändliga uppsättningar har samma kardinalitet. Till exempel visade Georg Cantor (som introducerade detta koncept) att de reella talen inte kan sättas i en-till-en-korrespondens med de naturliga talen (icke-negativa heltal), och därför att uppsättningen av reella tal har en större kardinalitet än uppsättningen naturliga tal.

Formell översikt

Per definition, en uppsättning S är uppräknelig om det existerar en injektiv funktion f  : S → N från S till de naturliga talen N = {0, 1, 2, 3, ...}. Det betyder helt enkelt att varje element i S har motsvarighet till ett annat element i N .

Det kan verka naturligt att dela upp uppsättningarna i olika klasser: sätt ihop alla uppsättningar som innehåller ett element; alla uppsättningar som innehåller två element tillsammans; ...; Slutligen, sätt ihop alla oändliga uppsättningar och betrakta dem som samma storlek. Denna uppfattning är dock inte hållbar under den naturliga definitionen av storlek.

För att utveckla detta behöver vi konceptet en bijection . Även om en "bijektion" kan verka som ett mer avancerat koncept än ett tal, definierar den vanliga utvecklingen av matematik när det gäller uppsättningsteori funktioner före tal, eftersom de är baserade på mycket enklare uppsättningar. Det är här begreppet bijection kommer in: definiera korrespondensen

a ↔ 1, b ↔ 2, c ↔ 3

Eftersom varje element i { a , b , c } är parat med exakt ett element i {1, 2, 3}, och vice versa, definierar detta en bijektion.

Vi generaliserar nu denna situation; Vi definierar att två uppsättningar är av samma storlek, om och bara om det finns en sammanbindning mellan dem. För alla ändliga uppsättningar ger detta oss den vanliga definitionen av "samma storlek".

När det gäller oändliga uppsättningar, överväg uppsättningarna A = {1, 2, 3, ...}, mängden positiva heltal och B = {2, 4, 6, ...}, mängden jämna positiva heltal. Vi hävdar att enligt vår definition har dessa uppsättningar samma storlek, och att B därför är oändligt. Kom ihåg att för att bevisa detta måste vi visa en förening mellan dem. Detta kan uppnås med uppgiften n ↔ 2 n , så att

1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, ....

Som i det tidigare exemplet har varje element i A kopplats ihop med exakt ett element i B, och vice versa. Därför har de samma storlek. Detta är ett exempel på en uppsättning av samma storlek som en av dess rätta delmängder , vilket är omöjligt för ändliga uppsättningar.

På samma sätt är uppsättningen av alla ordnade par naturliga tal (den kartesiska produkten av två uppsättningar naturliga tal, N × N ) oändligt stor, vilket kan ses genom att följa en väg som den på bilden:

Den Cantor para funktionen tilldelar ett naturligt tal till varje par av naturliga tal

Den resulterande kartläggningen fortsätter enligt följande:

0 ↔ (0, 0), 1 ↔ (1, 0), 2 ↔ (0, 1), 3 ↔ (2, 0), 4 ↔ (1, 1), 5 ↔ (0, 2), 6 ↔ (3, 0), ....

Denna kartläggning täcker alla sådana beställda par.

Denna form av triangulära kartläggning rekursivt generaliserar till n - tupler av naturliga tal, dvs., ( a 1 , en 2 , en 3 , ..., en n ) där en i och n är naturliga tal, genom att upprepade gånger att avbilda de två första delarna av en n -dubbel till ett naturligt tal. Till exempel kan (0, 2, 3) skrivas som ((0, 2), 3). Sedan kartlägger (0, 2) till 5 så ((0, 2), 3) kartar till (5, 3), sedan (5, 3) kartor till 39. Eftersom en annan 2-tupel, det är ett par som t.ex. ( a , b ), kartor till ett annat naturligt tal, en skillnad mellan två n-tupler med ett enda element är tillräckligt för att säkerställa att n-tuplerna kartläggs till olika naturliga nummer. Så, en injektion från uppsättningen n -dubblar till uppsättningen naturliga tal N är bevisad. För uppsättningen n-tupler gjorda av den kartesiska produkten av oändligt många olika uppsättningar, har varje element i varje tupel motsvarigheten till ett naturligt tal, så varje tupel kan skrivas i naturliga tal och samma logik tillämpas för att bevisa satsen .

Sats: Den kartesiska produkten av oändligt många räknbara uppsättningar kan räknas.

Uppsättningen av alla heltal Z och mängden av alla rationella tal Q kan intuitivt verkar mycket större än N . Men utseende kan lura. Om ett par behandlas som täljare och nämnare för en vulgär fraktion (en bråk i form av a / b där a och b ≠ 0 är heltal), kan vi för varje positiv bråk komma med ett distinkt naturligt tal som motsvarar till den. Denna representation inkluderar också de naturliga talen, eftersom varje naturligt tal också är en bråkdel N /1. Så vi kan dra slutsatsen att det finns exakt lika många positiva rationella tal som det finns positiva heltal. Detta gäller också för alla rationella tal, som kan ses nedan.

Sats: Z (uppsättningen av alla heltal) och Q (uppsättningen av alla rationella tal) kan räknas.

På ett liknande sätt är uppsättningen algebraiska tal räknbara.

Ibland är mer än en kartläggning användbar: en uppsättning A som ska visas som räkningsbar är en-till-en-mappad (injektion) till en annan uppsättning B, då visas A som räknbart om B är en-till-en-mappad till uppsättningen av naturliga tal. Till exempel kan uppsättningen positiva rationella tal enkelt vara en-till-en mappad till uppsättningen naturliga talpar (2-tupler) eftersom p / q kartlägger till ( p , q ). Eftersom uppsättningen naturliga talpar är en-till-en-mappad (faktiskt en-till-en-korrespondens eller bijektion) till uppsättningen naturliga tal som visas ovan, bevisas den positiva rationella taluppsättningen som räknbar.

Sats: Varje ändlig förening av räknbara uppsättningar kan räknas.

Med förutseende av att veta att det finns otaliga uppsättningar kan vi undra om detta sista resultat kan skjutas ytterligare. Svaret är "ja" och "nej", vi kan förlänga det, men vi måste anta ett nytt axiom för att göra det.

Sats: (Antar axiomet för det räknebara valet ) Föreningen av otaligt många räkningsbara uppsättningar kan räknas.

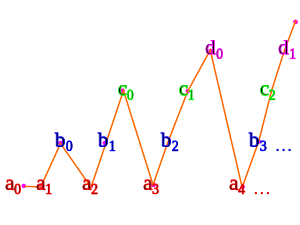
Till exempel, givet räknbara uppsättningar a , b , c , ...

Uppräkning för räkningsbart antal räkningsbara uppsättningar

Med hjälp av en variant av den triangulära uppräkningen som vi såg ovan:

  • a 0 kartar till 0
  • a 1 kartar till 1
  • b 0 kartor till 2
  • a 2 kartor till 3
  • b 1 kartor till 4
  • c 0 kartor till 5
  • a 3 kartor till 6
  • b 2 kartor till 7
  • c 1 kartor till 8
  • d 0 kartor till 9
  • a 4 kartor till 10
  • ...

Detta fungerar bara om uppsättningarna a , b , c , ... är osammanhängande . Om inte, så är facket ännu mindre och kan därför också räknas med en tidigare sats.

Vi behöver axiomet med det räknade valet för att indexera alla uppsättningarna a , b , c , ... samtidigt.

Sats: Uppsättningen av alla ändliga sekvenser av naturliga tal kan räknas.

Denna uppsättning är föreningen av längden-1-sekvenserna, längden-2-sekvenserna, längden-3-sekvenserna, som var och en är en räkningsbar uppsättning (ändlig kartesisk produkt). Så vi pratar om en räkningsbar förening av räkningsbara uppsättningar, som kan räknas med föregående sats.

Sats: Uppsättningen av alla ändliga delmängder av de naturliga siffrorna kan räknas.

Elementen i en ändlig delmängd kan ordnas i en ändlig sekvens. Det finns bara otaligt många ändliga sekvenser, så det finns också bara otaligt många ändliga delmängder.

Sats: Låt S och T vara uppsättningar.

  1. Om funktionen f  : S → T är injektiv och T kan räknas, är S att räkna.
  2. Om funktionen g  : S → T är surjektiv och S kan räknas är T räknas.

Dessa följer av definitionerna av räkningsbara uppsättningar som injektiva / surjektiva funktioner.

Cantors sats hävdar att om A är en uppsättning och P ( A ) är dess effektuppsättning , dvs uppsättningen för alla delmängder av A , så finns det ingen surjektiv funktion från A till P ( A ). Ett bevis ges i artikeln Cantors sats . Som en omedelbar konsekvens av detta och grundsatsen ovan har vi:

Proposition: Uppsättningen P ( N ) kan inte räknas; dvs det är otaligt .

För en utarbetande av detta resultat se Cantors diagonala argument .

Uppsättningen av verkliga tal är otaliga, och så är uppsättningen med alla oändliga sekvenser av naturliga tal.

Minimal modell av uppsättningsteori kan räknas

Om det finns en uppsättning som är en standardmodell (se inre modell ) för ZFC -uppsättningsteori, så finns det en minimal standardmodell ( se Konstruerbart universum ). Den Lowenheim-Skolem sats kan användas för att visa att denna minimala modell är kvantifierbart. Det faktum att begreppet "otalighet" är meningsfullt även i denna modell, och i synnerhet att denna modell M innehåller element som är:

  • delmängder av M , därför räknade,
  • men oräknelig ur M: s synvinkel ,

betraktades som paradoxalt i början av uppsättningsteorin, se Skolems paradox för mer.

Den minimala standardmodellen innehåller alla algebraiska tal och alla effektivt beräkningsbara transcendentala tal , liksom många andra sorters tal.

Totala order

Räkningsbara uppsättningar kan beställas totalt på olika sätt, till exempel:

  • Brunnordningar (se även ordningsnummer ):
    • Den vanliga ordningen för naturliga tal (0, 1, 2, 3, 4, 5, ...)
    • Heltalen i ordningen (0, 1, 2, 3, ...; −1, −2, −3, ...)
  • Andra ( inte bra beställningar):
    • Den vanliga ordningen för heltal (..., −3, −2, −1, 0, 1, 2, 3, ...)
    • Den vanliga ordningen med rationella tal (Kan inte uttryckligen skrivas som en ordnad lista!)

I båda exemplen på brunnordningar här har varje delmängd ett minst element ; och i båda exemplen på icke-brunnorder har vissa delmängder inte det minsta elementet . Detta är den centrala definitionen som avgör om en total order också är en brunnorder.

Se även

Anteckningar

Citat

Referenser