Överlevnadsfunktion - Survival function

Den överlevnadsfunktion är en funktion som ger sannolikheten att en patient, enhet eller annat föremål av intresse kommer att överleva längre än någon angiven tid.

Överlevnadsfunktionen är också känd som överlevnadsfunktionen eller tillförlitlighetsfunktionen .

Uttrycket tillförlitlighetsfunktion är vanligt inom teknik medan termen överlevnadsfunktion används i ett bredare spektrum av tillämpningar, inklusive mänsklig dödlighet. Ett annat namn för överlevnadsfunktionen är den kompletterande kumulativa fördelningsfunktionen .

Definition

Låt T vara en kontinuerlig slumpmässig variabel med kumulativ fördelningsfunktion F ( t ) på intervallet [0, ∞). Dess överlevnadsfunktion eller tillförlitlighetsfunktion är:

{\ displaystyle S (t) = P (\ {T> t \}) ​​= \ int _ {t} ^ {\ infty} f (u) \, du = 1-F (t).}

Exempel på överlevnadsfunktioner

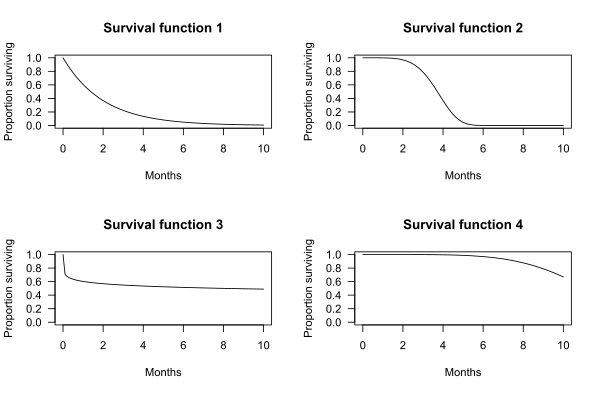
Diagrammen nedan visar exempel på hypotetiska överlevnadsfunktioner. X-axeln är tid. Y-axeln är andelen försökspersoner som överlever. Diagrammen visar sannolikheten för att ett ämne kommer att överleva utöver tiden t.

Till exempel, för överlevnadsfunktion 1 är sannolikheten att överleva längre än t = 2 månader 0,37. Det vill säga 37% av patienterna överlever mer än två månader.

För överlevnadsfunktion 2 är sannolikheten att överleva längre än t = 2 månader 0,97. Det vill säga 97% av patienterna överlever mer än två månader.

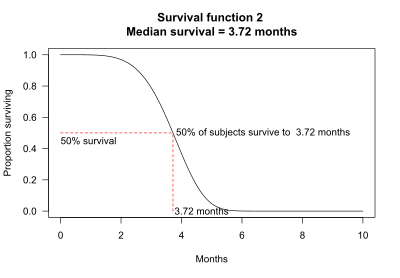
Medianöverlevnad kan bestämmas utifrån överlevnadsfunktionen. Till exempel, för överlevnadsfunktion 2 överlever 50% av försökspersonerna 3,72 månader. Medianöverlevnaden är således 3,72 månader.

I vissa fall kan medianöverlevnad inte bestämmas från diagrammet. Till exempel, för överlevnadsfunktion 4, överlever mer än 50% av försökspersonerna längre än observationsperioden på 10 månader.

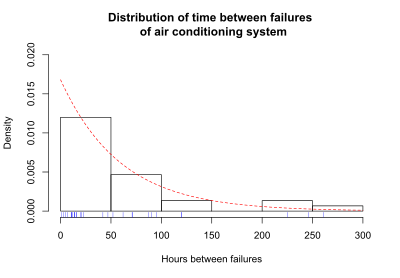
Överlevnadsfunktionen är ett av flera sätt att beskriva och visa överlevnadsdata. Ett annat användbart sätt att visa data är en graf som visar fördelningen av överlevnadstider hos försökspersoner. Olkin, sidan 426, ger följande exempel på överlevnadsdata. Antalet timmar mellan successiva fel i ett luftkonditioneringssystem registrerades. Tiden mellan efterföljande fel är 1, 3, 5, 7, 11, 11, 11, 12, 14, 14, 14, 16, 16, 20, 21, 23, 42, 47, 52, 62, 71, 71, 87, 90, 95, 120, 120, 225, 246 och 261 timmar. Medeltiden mellan fel är 59,6. Detta medelvärde kommer snart att användas för att anpassa en teoretisk kurva till data. Figuren nedan visar fördelningen av tiden mellan fel. De blå bockmarkeringarna under diagrammet är de faktiska timmarna mellan på varandra följande misslyckanden.

Fördelningen av fel gånger är överlagd med en kurva som representerar en exponentiell fördelning. I det här exemplet approximerar den exponentiella fördelningen fördelningen av fel gånger. Den exponentiella kurvan är en teoretisk fördelning anpassad till de faktiska felfunktionerna. Denna specifika exponentiella kurva specificeras av parametern lambda, λ = 1 / (genomsnittlig tid mellan fel) = 1 / 59,6 = 0,0168. Fördelningen av felstunder kallas sannolikhetsdensitetsfunktionen (pdf), om tiden kan ta något positivt värde. I ekvationer specificeras pdf som f (t). Om tiden bara kan ta diskreta värden (som 1 dag, 2 dagar och så vidare) kallas fördelningen av felstunder sannolikhetsfunktionen (pmf). De flesta metoder för överlevnadsanalys förutsätter att tiden kan ta något positivt värde, och f (t) är pdf. Om tiden mellan observerade luftkonditioneringsfel approximeras med hjälp av den exponentiella funktionen, ger den exponentiella kurvan sannolikhetsdensitetsfunktionen, f (t), för luftkonditioneringens misslyckande gånger.

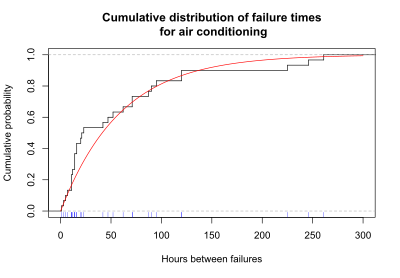
Ett annat användbart sätt att visa överlevnadsdata är en graf som visar de kumulativa misslyckandena upp till varje tidpunkt. Dessa data kan visas antingen som det kumulativa antalet eller den kumulativa andelen fel upp till varje gång. Diagrammet nedan visar den kumulativa sannolikheten (eller andelen) av fel vid varje gång för luftkonditioneringssystemet. Trappstegslinjen i svart visar den kumulativa andelen fel. För varje steg finns det en blå bock längst ner i diagrammet som indikerar en observerad feltid. Den släta röda linjen representerar den exponentiella kurvan som passar de observerade data.

En graf över den kumulativa sannolikheten för fel upp till varje tidpunkt kallas den kumulativa fördelningsfunktionen , eller CDF. I överlevnadsanalys ger den kumulativa fördelningsfunktionen sannolikheten att överlevnadstiden är mindre än eller lika med en viss tid, t.

Låt T vara överlevnadstid, vilket är något positivt tal. En viss tid anges med gemener t. Den kumulativa fördelningsfunktionen för T är funktionen

{\ displaystyle F (t) = \ operatorname {P} (T \ leq t),}

där höger sida representerar sannolikheten att den slumpmässiga variabeln T är mindre än eller lika med t . Om tiden kan ta något positivt värde är den kumulativa fördelningsfunktionen F (t) integralen av sannolikhetsdensitetsfunktionen f (t).

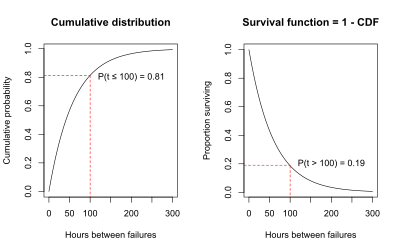
För luftkonditioneringsexemplet illustrerar grafen för CDF nedan att sannolikheten för att tiden till fel är mindre än eller lika med 100 timmar är 0,81, uppskattad med användning av den exponentiella kurvan som passar data.

Ett alternativ till att kartlägga sannolikheten att feltiden är mindre än eller lika med 100 timmar är att diagram sannolikheten för att feltiden är längre än 100 timmar. Sannolikheten att feltiden är större än 100 timmar måste vara 1 minus sannolikheten att feltiden är mindre än eller lika med 100 timmar, eftersom den totala sannolikheten måste uppgå till 1.

Detta ger

P (feltid> 100 timmar) = 1 - P (feltid <100 timmar) = 1 - 0,81 = 0,19.

Detta förhållande generaliserar till alla misslyckanden:

P (T> t) = 1 - P (T <t) = 1 - kumulativ fördelningsfunktion.

Detta förhållande visas i diagrammen nedan. Grafen till vänster är den kumulativa fördelningsfunktionen, som är P (T <t). Grafen till höger är P (T> t) = 1 - P (T <t). Grafen till höger är överlevnadsfunktionen, S (t). Det faktum att S (t) = 1 - CDF är anledningen till att ett annat namn för överlevnadsfunktionen är den kompletterande kumulativa fördelningsfunktionen.

Parametriska överlevnadsfunktioner

I vissa fall, såsom exempelvis luftkonditioneringsapparaten, kan fördelningen av överlevnadstiderna approximeras väl med en funktion som exponentiell fördelning. Flera distributioner används vanligtvis i överlevnadsanalys, inklusive den exponentiella, Weibull, gamma, normal, log-normal och log-logistik. Dessa fördelningar definieras av parametrar. Den normala (Gaussiska) fördelningen definieras till exempel av de två parametrarna medelvärde och standardavvikelse. Överlevnadsfunktioner som definieras av parametrar sägs vara parametriska.

I de fyra överlevnadsfunktionsdiagrammen som visas ovan definieras överlevnadsfunktionens form av en viss sannolikhetsfördelning: överlevnadsfunktion 1 definieras av en exponentiell fördelning, 2 definieras av en Weibull-fördelning, 3 definieras av en loglogistisk fördelning och 4 definieras av en annan Weibull-distribution.

Exponentiell överlevnadsfunktion

För en exponentiell överlevnadsfördelning är sannolikheten för misslyckande densamma i varje tidsintervall, oavsett individens eller enhetens ålder. Detta faktum leder till den "minneslösa" egenskapen hos den exponentiella överlevnadsfördelningen: en persons ålder har ingen effekt på sannolikheten för misslyckande i nästa tidsintervall. Exponentialen kan vara en bra modell under ett systems livslängd där delar byts ut när de misslyckas. Det kan också vara användbart för att modellera överlevnad av levande organismer under korta intervaller. Det är inte troligt att det är en bra modell för en levande organisms hela livslängd. Som Efron och Hastie (s. 134) konstaterar, "Om mänskliga livstider var exponentiella skulle det inte finnas gamla eller unga människor, bara tur eller otur".

Weibull-överlevnadsfunktion

Ett viktigt antagande av den exponentiella överlevnadsfunktionen är att riskfrekvensen är konstant. I ovanstående exempel var andelen män som dör varje år konstant på 10%, vilket innebär att riskfrekvensen var konstant. Antagandet om konstant fara kanske inte är lämpligt. Bland de flesta levande organismer är risken för död till exempel större vid ålderdomen än i medelåldern - det vill säga riskfrekvensen ökar med tiden. För vissa sjukdomar, såsom bröstcancer, är risken för återfall lägre efter 5 år - det vill säga riskfrekvensen minskar med tiden. Den Weibull fördelningen sträcker exponentialfördelningen att tillåta konstant, ökar eller minskar risk priser.

Andra parametriska överlevnadsfunktioner

Det finns flera andra parametriska överlevnadsfunktioner som kan ge en bättre anpassning till en viss datamängd, inklusive normal, lognormal, loglogistisk och gamma. Valet av parametrisk fördelning för en viss applikation kan göras med hjälp av grafiska metoder eller med formella test av passform. Dessa distributioner och tester beskrivs i läroböcker om överlevnadsanalys. Lawless har omfattande täckning av parametriska modeller.

Parametriska överlevnadsfunktioner används ofta i tillverkningsapplikationer, delvis för att de möjliggör uppskattning av överlevnadsfunktionen efter observationsperioden. Lämplig användning av parametriska funktioner kräver dock att data modelleras väl av den valda distributionen. Om en lämplig distribution inte är tillgänglig, eller inte kan specificeras före en klinisk prövning eller experiment, erbjuder icke-parametriska överlevnadsfunktioner ett användbart alternativ.

Icke-parametriska överlevnadsfunktioner

En parametrisk överlevnadsmodell kanske inte är möjlig eller önskvärd. I dessa situationer är den vanligaste metoden för att modellera överlevnadsfunktionen den icke-parametriska uppskattaren Kaplan – Meier .

Egenskaper

Varje överlevnadsfunktion är monotont minskar
, det vill säga för alla . ${\ displaystyle S (t)}$ $S (t)$ ${\ displaystyle S (u) \ leq S (t)}$ $S (u) \ leq S (t)$ ${\ displaystyle u> t}$ $u> t$
- Det är en egenskap hos en slumpmässig variabel som kartlägger en uppsättning händelser, vanligtvis förknippade med dödlighet eller misslyckande i något system, på tiden .
Den tid , representerar en viss ursprung, vanligtvis i början av en studie eller i början av driften av något system. är vanligtvis enhet men kan vara mindre för att representera sannolikheten för att systemet misslyckas omedelbart efter drift. ${\ displaystyle t = 0}$ ${\ displaystyle S (0)}$
Eftersom CDF är en rätt-kontinuerlig funktion är överlevnadsfunktionen också rätt-kontinuerlig. ${\ displaystyle S (t) = 1-F (t)}$
Överlevnadsfunktionen kan relateras till sannolikhetsdensitetsfunktionen och riskfunktionen ${\ displaystyle f (t)}$ $med)$ ${\ displaystyle \ lambda (t)}$ $\ lambda (t)$
- ${\ displaystyle f (t) = - S '(t)}$
- ${\ displaystyle \ lambda (t) = - {d \ over {dt}} \ log S (t)}$

Så att ${\ displaystyle S (t) = \ exp [- \ int _ {0} ^ {t} \ lambda (t ') dt']}$

Den förväntade överlevnadstiden ${\ displaystyle \ mathbb {E} (T) = \ int _ {0} ^ {\ infty} S (t) dt}$

Bevis på förväntad formel för överlevnadstid

Det förväntade värdet på en slumpmässig variabel definieras som:

{\ displaystyle T \ in [0, \ infty)}

{\ displaystyle \ mathbb {E} (T) = \ int _ {0} ^ {\ infty} tf (t) dt}

var är sannolikhetsdensitetsfunktionen . Med hjälp av relationen kan den förväntade formeln modifieras: ${\ displaystyle f (t)}$ ${\ displaystyle f (t) = - S '(t)}$

{\ displaystyle \ mathbb {E} (T) = - \ int _ {0} ^ {\ infty} tS '(t) dt}

Detta kan förenklas ytterligare genom att använda integration av delar :

{\ displaystyle - \ int _ {0} ^ {\ infty} tS '(t) dt = -tS (t) {\ bigg |} _ {0} ^ {\ infty} + \ int _ {0} ^ { \ infty} S (t) dt}

Per definition, vilket innebär att gränsvillkoren är identiskt lika med noll. Därför kan vi dra slutsatsen att det förväntade värdet helt enkelt är integralen i överlevnadsfunktionen: ${\ displaystyle S (\ infty) = 0}$

{\ displaystyle \ mathbb {E} (T) = \ int _ {0} ^ {\ infty} S (t) dt}

Languages

In other projects