Udda graf - Odd graph
| Udda graf | |
|---|---|
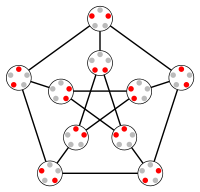
O 3 = KG 5,2 är Petersen -grafen
| |
| Hörn | |
| Kanter | |
| Diameter | n - 1 |
| Omkrets | 3 om n = 2 5 om n = 3 6 om n > 3 |
| Egenskaper | Avståndstransitiv |
| Notation | O n |
| Tabell över grafer och parametrar | |
I det matematiska området grafteori är de udda graferna O n en familj av symmetriska grafer med hög udda omkrets , definierade från vissa uppsatta system . De inkluderar och generaliserar Petersen -grafen .
Definition och exempel
Den udda grafen O n har en toppunkt för var och en av ( n- 1) -elementundermängderna i en (2 n- 1) -elementuppsättning. Två hörn är anslutna med en kant om och endast om motsvarande delmängder är oskarv . Det vill säga O n är Kneser -grafen KG (2 n - 1, n - 1).
O 2 är en triangel, medan O 3 är den välkända Petersen -grafen .
De generaliserade udda graferna definieras som avståndsregelbundna grafer med diameter n- 1 och udda omkrets 2 n- 1 för några n . De inkluderar udda grafer och de vikta kubgraferna .
Historia och applikationer
Även om Petersen -grafen har varit känd sedan 1898, är definitionen som en udda graf daterad till arbetet från Kowalewski (1917) , som också studerade den udda grafen O 4 . Udda grafer har studerats för deras tillämpningar inom kemisk grafteori , vid modellering av skiftningarna av karboniumjoner . De har också föreslagits som en nätverkstopologi i parallell databehandling .
Notationen O n för dessa grafer introducerades av Norman Biggs 1972. Biggs och Tony Gardiner förklarar namnet på udda grafer i ett opublicerat manuskript från 1974: varje kant på ett udda diagram kan tilldelas det unika elementet i X som är " udda man ut ", dvs inte medlem i någon av delmängderna associerade med hörnen som inträffar till den kanten.
Egenskaper
Den udda grafen O n är regelbunden för graden n . Den har hörn och kanter. Därför är antalet hörn för n = 1, 2, ...
Avstånd och symmetri
Om två hörn i O n motsvarar uppsättningar som skiljer sig från varandra genom avlägsnande av k -element från en uppsättning och tillsats av k olika element, kan de nås från varandra i 2 k -steg, vars par utför en enda tillsats och borttagning. Om 2 k < n är detta en kortaste väg ; annars är det kortare att hitta en väg av denna typ från den första uppsättningen till en uppsättning som kompletterar den andra, och sedan nå den andra uppsättningen i ytterligare ett steg. Därför diametern hos O n är n - 1.
Varje udda graf är 3-båg-transitiv : varje riktad trekantig väg i en udda graf kan omvandlas till varannan sådan väg genom en symmetri av grafen. Udda grafer är avståndstransitiva , därav regelbundna avstånd . Som avståndsregelbundna grafer definieras de unikt av deras korsningsarray: inga andra avståndsregelbundna grafer kan ha samma parametrar som ett udda diagram. Men trots sin höga symmetri är de udda graferna O n för n > 2 aldrig Cayley -grafer .
Eftersom udda grafer är regelbundna och kanttransitiva är deras toppunktsanslutning lika med graden, n .
Udda grafer med n > 3 har omkrets sex; även om de inte är tvåpartsdiagram är deras udda cykler mycket längre. Specifikt, den udda graf O n har udda omkrets 2 n - 1. Om en n -regular graf har diameter n - 1 och udda omkrets 2 n - 1, och har endast n distinkta egenvärden , måste det vara avstånd-regelbundna. Avståndsregelbundna grafer med diameter n- 1 och udda omkrets 2 n- 1 är kända som de generaliserade udda graferna och inkluderar de vikta kubgraferna samt de udda graferna själva.
Oberoende uppsättningar och vertexfärgning
Låt O n vara ett udda graf definierad från undergrupper av en (2 n - 1) -element uppsättning X , och låt x vara någon medlem av X . Bland hörnen på O n motsvarar exakt hörn uppsättningar som innehåller x . Eftersom alla dessa set innehåller x , de är inte disjunkta, och bildar en oberoende uppsättning av O n . Det vill säga O n har 2 n - 1 olika oberoende uppsättningar av storlek . Det följer av Erdős – Ko – Rado -satsen att dessa är de maximala oberoende uppsättningarna av O n . dvs oberoende antalet av O n är Vidare måste varje maximal oberoende uppsättning har denna form, så O n har exakt 2 n - 1 maximala oberoende uppsättningar.
Om I är en maximal oberoende uppsättning, som bildas av de uppsättningar som innehåller x , är komplementet för I den uppsättning hörn som inte innehåller x . Denna kompletterande uppsättning framkallar en matchning i G . Varje hörn i den oberoende uppsättningen ligger intill matchningens n hörn, och varje hörn av matchningen ligger intill n - 1 hörn av den oberoende uppsättningen. På grund av denna sönderdelning och eftersom udda grafer inte är tvåpartiga har de kromatisk nummer tre: hörnen för den maximala oberoende uppsättningen kan tilldelas en enda färg och ytterligare två färger räcker för att färga den kompletterande matchningen.
Kantfärgning
Enligt Vizinges sats är antalet färger som behövs för att färga kanterna på udda grafen O n antingen n eller n + 1, och i fallet med Petersen -grafen O 3 är det n + 1. När n är en effekt på två , antalet hörn i grafen är udda, varifrån det återigen följer att antalet kantfärger är n + 1. Emellertid kan O 5 , O 6 och O 7 var och en vara kantfärgade med n färger.
Biggs förklarar detta problem med följande historia: elva fotboll spelare i den fiktiva staden Croam önskan att bilda upp par av fem man team (med en särling att fungera som domare) i alla 1386 möjliga sätt, och de vill schema matcherna mellan varje par på ett sådant sätt att de sex matcherna för varje lag spelas på sex olika dagar i veckan, med söndagar lediga för alla lag. Är det möjligt att göra det? I denna berättelse representerar varje spel en kant på O 6 , varje vardag representeras av en färg och en 6-färgad kantfärgning av O 6 ger en lösning på spelarnas schemaläggningsproblem.
Hamiltonicitet
Petersen-grafen O 3 är en välkänd icke-Hamiltonisk graf, men alla udda grafer O n för n ≥ 4 är kända för att ha en hamiltons cykel. Eftersom de udda graferna är vertex-transitiva är de således ett av de specialfall för vilka ett positivt svar på Lovász gissning är känt. Biggs gissade mer allmänt att kanterna på O n kan delas upp i kantskilda Hamiltoniska cykler. När n är udda måste de kvarvarande kanterna sedan bilda en perfekt matchning. Denna starkare gissning verifierades för n = 4, 5, 6, 7. För n = 8 förhindrar det udda antalet hörn i O n att en 8-färgad kantfärgning existerar, men utesluter inte möjligheten att partitioneras i fyra hamiltons cykler.






