Maxflöde min-cut sats- Max-flow min-cut theorem

I datorvetenskap och optimeringslära , de max-flöde, minsta-snitt anges att i ett flödesnätverk , den maximala mängden flöde som passerar från källan till diskhon är lika med den totala vikten av kanterna i en minimi skuren , dvs. minsta totala vikt av kanterna som om de tas bort skulle koppla bort källan från diskbänken.

Detta är ett specialfall av dualitetsteoremet för linjära program och kan användas för att härleda Mengers sats och Kőnig – Egerváry -satsen .

Definitioner och uttalande

Satsen avser två kvantiteter: det maximala flödet genom ett nätverk och minimikapaciteten för en kapning av nätverket, det vill säga minimikapaciteten uppnås genom flödet.

För att ange satsen måste var och en av dessa kvantiteter först definieras.

Låt $N = (V, E)$ vara en riktad graf , där V betecknar uppsättningen hörn och E är uppsättningen kanter. Låt $s \in V$ och $t \in V$ vara källan och sink av $N$ , respektive.

Den kapacitet av en kant är en mappning betecknas med $c$ $uv$ eller $c$ $($ $u$ $,$ $v$ $)$ , där $u$ $,$ $v$ $\in$ $V$ . Det representerar den maximala mängden flöde som kan passera genom en kant. $c:E\to \mathbb {R} ^{+}$

Flöden

Ett flöde är en mappning betecknad med eller , med förbehåll för följande två begränsningar: $f:E\to \mathbb {R} ^{+}$ $f_{uv}$ $f(u,v)$

Kapacitetsbegränsning : För varje kant , $(u,v)\in E$ $f_{uv}\leq c_{uv}.$
Bevarande av flöden : För varje hörn bortsett från och (dvs. källan respektive sinken ) gäller följande jämlikhet: $v$ $s$ $t$
$\sum \nolimits _{\{u:(u,v)\in E\}}f_{uv}=\sum \nolimits _{\{w:(v,w)\in E\}}f_{vw}.$

Ett flöde kan visualiseras som ett fysiskt flöde av en vätska genom nätverket, efter riktningen för varje kant. Kapacitetsbegränsningen säger sedan att volymen som flödar genom varje kant per tidsenhet är mindre än eller lika med kantens maximala kapacitet, och bevarandebegränsningen säger att mängden som flyter in i varje hörn är lika med mängden som strömmar ut från varje hörn, bortsett från käll- och sjunkpunkten.

Det värde av ett flöde definieras av

|f|=\sum \nolimits _{\{v:(s,v)\in E\}}f_{sv}=\sum \nolimits _{\{v:(v,t)\in E\}}f_{vt},

där som ovan är källnoden och är sinknoden . I vätskeanalogin representerar den mängden vätska som kommer in i nätverket vid källnoden. På grund av bevarandeaxiom för flöden är detta detsamma som mängden flöde som lämnar nätet vid sinknoden. $s$ $t$

Problemet med maximalt flöde ber om det största flödet i ett givet nätverk.

Maximalt flödesproblem. Maximera, det vill säga att dirigera så mycket flöde som möjligt fråntill. $|f|$ $s$ $t$

Nedskärningar

Den andra halvan av maxflödet min-cut-satsen refererar till en annan aspekt av ett nätverk: samlingen av nedskärningar. En st cut $C = (S, T)$ är en partition av $V$ så att $s \in S$ och $t \in T$ . Det vill säga s - t cut är en uppdelning av nätverkets hörn i två delar, med källan i en del och sinken i den andra. Den cut-uppsättning av en skuren $C$ är den uppsättning av kanter som ansluter källan del av snittet till sink delen: $X_{C}$

X_{C}:=\{(u,v)\in E\ :\ u\in S,v\in T\}=(S\times T)\cap E.

Således, om alla kanterna i snittuppsättningen för $C$ tas bort, är inget positivt flöde möjligt, eftersom det inte finns någon väg i den resulterande grafen från källan till diskbänken.

Den kapacitet av en st snitt är summan av kapaciteten hos de kanter i det sneda set,

c(S,T)=\sum \nolimits _{(u,v)\in X_{C}}c_{uv}=\sum \nolimits _{(i,j)\in E}c_{ij}d_{ij},

där om och , i övrigt. $d_{ij}=1$ $i\in S$ $j\in T$ $0$

Det finns vanligtvis många snitt i en graf, men snitt med mindre vikter är ofta svårare att hitta.

Minsta st Klippproblem. Minimera

c (S, T)

, det vill säga bestämma

S

och

T

så att kapaciteten hos ST -snittet är minimal.

Huvudsats

Huvudsatsen kopplar det maximala flödet genom ett nätverk med minsta möjliga nedskärning av nätverket.

Maxflöde min-cut sats. Det maximala värdet för ett st -flöde är lika med minsta kapacitet över alla st -snitt.

Linjär programformulering

Maxflödesproblemet och min-cut-problemet kan formuleras som två primal-dubbla linjära program.

	Maxflöde (Primal)	Minskuren (dubbel)
variabler	$f_{uv}$ $\forall (u,v)\in E$ [en variabel per kant]	$d_{uv}$ $\forall (u,v)\in E$ [en variabel per kant] $z_{v}$ $\forall v\in V\setminus \{s,t\}$ [en variabel per icke-terminal nod]
mål	maximera $\sum \nolimits _{v:(s,v)\in E}f_{sv}$ [max totalt flöde från källa]	minimera $\sum \nolimits _{(u,v)\in E}c_{uv}d_{uv}$ [min total kapacitet för kanter i snitt]
begränsningar	föremål för ${\begin{aligned}f_{uv}&\leq c_{uv}&&\forall (u,v)\in E\\\sum _{u}f_{uv}-\sum _{w}f_{vw}&=0&&v\in V\setminus \{s,t\}\end{aligned}}$ [en begränsning per kant och en begränsning per icke-terminal nod]	föremål för ${\begin{aligned}d_{uv}-z_{u}+z_{v}&\geq 0&&\forall (u,v)\in E,u\neq s,v\neq t\\d_{sv}+z_{v}&\geq 1&&\forall (s,v)\in E\\d_{ut}-z_{u}&\geq 0&&\forall (u,t)\in E,u\neq s\\\end{aligned}}$ [en begränsning per kant]
teckenbegränsningar	${\begin{aligned}f_{uv}&\geq 0&&\forall (u,v)\in E\\\end{aligned}}$	${\begin{aligned}d_{uv}&\geq 0&&\forall (u,v)\in E\\z_{v}&\in \mathbb {R} &&\forall v\in V\setminus \{s,t\}\end{aligned}}$

Maxflödet LP är enkelt. Den dubbla LP erhålls med hjälp av algoritmen som beskrivs i dubbel linjärt program . Den resulterande LP kräver lite förklaring. Tolkningen av variablerna i min-cut LP är:

d_{uv}={\begin{cases}1,&{\text{if }}u\in S{\text{ and }}v\in T{\text{ (the edge }}uv{\text{ is in the cut) }}\\0,&{\text{otherwise}}\end{cases}}

z_{u}={\begin{cases}1,&{\text{if }}u\in S\\0,&{\text{otherwise}}\end{cases}}

Minimeringsmålet summerar kapaciteten över alla kanter som finns i snittet.

Begränsningarna garanterar att variablerna verkligen representerar en juridisk nedskärning:

Begränsningarna (motsvarande ) garanterar att för icke-terminala noder u, v , om u är i S och v är i T , räknas kanten ( u , v ) i snittet ( ). $d_{uv}-z_{u}+z_{v}\geq 0$ $d_{uv}\geq z_{u}-z_{v}$ $d_{uv}\geq 1$
Begränsningarna (motsvarande ) garanterar att, om v är i T , räknas kanten (s, v) i snittet (eftersom s per definition är i S ). $d_{sv}+z_{v}\geq 1$ $d_{sv}\geq 1-z_{v}$
Begränsningarna (motsvarande ) garanterar att, om u är i S , räknas kanten (u, t) i snittet (eftersom t per definition är i T ). $d_{ut}-z_{u}\geq 0$ $d_{ut}\geq z_{u}$

Observera att eftersom detta är ett minimeringsproblem behöver vi inte garantera att en kant inte är i snittet - vi måste bara garantera att varje kant som ska vara i snittet summeras i objektfunktionen.

Jämställdheten i maxflödesminskningssatsen följer av den starka dualitetsteoremet i linjär programmering , som säger att om det primära programmet har en optimal lösning, x *, så har dubbelprogrammet också en optimal lösning, y *, sådan att de optimala värdena som bildas av de två lösningarna är lika.

Exempel

Ett nätverk med ett flödesvärde som är lika med kapaciteten för ett första snitt

Figuren till höger är ett nätverk med ett flödesvärde på 7. Den numeriska kommentaren på varje pil, i formen x / y , indikerar flödet ( x ) och kapaciteten ( y ). Flödena som kommer från källan är totalt sju (4+3 = 7), liksom flödena i diskhon (3+4 = 7).

Spetsen i vitt och hörnen i grått bildar delmängderna $S$ och $T$ för ett st snitt, vars snittuppsättning innehåller de streckade kanterna. Eftersom kapaciteten för st-snittet är 7, vilket motsvarar flödesvärdet, indikerar max-flödets min-cut-sats att värdet på flödet och kapaciteten för st-snittet båda är optimala i detta nätverk.

Observera att flödet genom var och en av de streckade kanterna har full kapacitet: detta är systemets "flaskhals". Däremot finns det ledig kapacitet i den högra delen av nätverket. I synnerhet behöver flödet från nod en till nod två inte vara lika med 1. Om det inte fanns något flöde mellan noderna en och två, skulle ingångarna till diskhon ändras till 4/4 och 3/5; det totala flödet skulle fortfarande vara sju (4+3 = 7). Å andra sidan, om flödet från nod en till nod två fördubblades till 2, skulle ingångarna till diskhon ändras till 2/4 och 5/5; det totala flödet skulle återigen ligga kvar på sju (2+5 = 7).

Ansökan

Cederbaums maximal flödesats

Maxflödesproblemet kan formuleras som maximering av den elektriska strömmen genom ett nätverk som består av olinjära resistiva element. I denna formulering, gränsen för strömmen $I$ $i$ mellan ingångsuttagen hos det elektriska nätet som ingångsspänningen $V$ $i$ tillvägagångssätt , är lika med vikten av den minsta vikt cut set. $\infty$

\lim _{V_{\text{in}}\to \infty }(I_{in})=\min _{X_{C}}\sum _{(u,v)\in X_{C}}c_{uv}

Generaliserat maxflöde min-cut sats

Förutom kantkapacitet, tänk på att det finns kapacitet vid varje toppunkt, det vill säga en kartläggning betecknad med $c$ $($ $v$ $)$ , så att flödet $f$ måste uppfylla inte bara kapacitetsbegränsningen och bevarandet av flöden utan även toppunktskapaciteten begränsning $c:V\to \mathbb {R} ^{+}$

\forall v\in V\setminus \{s,t\}:\qquad \sum \nolimits _{\{u\in V\mid (u,v)\in E\}}f_{uv}\leq c(v).

Med andra ord kan mängden flöde som passerar genom en toppunkt inte överstiga dess kapacitet. Definiera ett st snitt som uppsättningen hörn och kanter så att för alla banor från s till t innehåller vägen en del av snittet. I detta fall kapaciteten hos snittet är summan kapacitet varje kant och vertex i den.

I denna nya definition anger den generaliserade max-flödet min-cut-satsen att maximivärdet för ett st-flöde är lika med minimikapaciteten för ett st-snitt i den nya meningen.

Mengers sats

I det icke riktad kant-disjunkta banor problemet, får vi en oriktad graf $G = (V, E)$ och två hörn $s$ och $t$ , och vi måste finna det maximala antalet kant disjunkta st banor i $G$ .

Den Menger teorem anger att det maximala antalet kant disjunkta st banor i en oriktad graf är lika med det minsta antalet kanter i ett st cut-set.

Projektvalsproblem

En nätverksformulering av projektvalsproblemet med den optimala lösningen

I projektvalsproblemet finns det $n$ projekt och $m$ maskiner. Varje projekt $p i$ ger intäkter $r (p i)$ och varje maskin $q j$ kostar $c (q j)$ att köpa. Varje projekt kräver ett antal maskiner och varje maskin kan delas av flera projekt. Problemet är att bestämma vilka projekt och maskiner som ska väljas respektive köpas, så att vinsten maximeras.

Låt $P$ vara den uppsättning projekt som inte valts och $Q$ vara uppsättningen maskiner som köpts, då kan problemet formuleras som,

\max\{g\}=\sum _{i}r(p_{i})-\sum _{p_{i}\in P}r(p_{i})-\sum _{q_{j}\in Q}c(q_{j}).

Eftersom den första termen inte beror på valet av $P$ och $Q$ , kan detta maximeringsproblem formuleras som ett minimeringsproblem istället, det vill säga

\min\{g'\}=\sum _{p_{i}\in P}r(p_{i})+\sum _{q_{j}\in Q}c(q_{j}).

Ovanstående minimeringsproblem kan sedan formuleras som ett minimiklipproblem genom att konstruera ett nätverk, där källan är ansluten till projekten med kapacitet $r (p i)$ , och sinken är ansluten av maskinerna med kapacitet $c (q j)$ . En kant $(p i, q j)$ med oändlig kapacitet läggs till om projekt $p i$ kräver maskin $q j$ . St cut-uppsättning representerar de projekt och maskiner i $P$ och $Q$ respektive. Genom maxflödet min-cut teorem kan man lösa problemet som ett maximalt flödesproblem .

Figuren till höger ger en nätverksformulering av följande projektvalsproblem:

	Projekt $r (p i)$	Maskin $c (q j)$
1	100	200	Projekt 1 kräver maskiner 1 och 2.
2	200	100	Projekt 2 kräver maskin 2.
3	150	50	Projekt 3 kräver maskin 3.

Minsta kapacitet för en första nedskärning är 250 och summan av intäkterna för varje projekt är 450; därför är den maximala vinsten g 450 - 250 = 200, genom att välja projekt $p 2$ och $p 3$ .

Tanken här är att "flöda" varje projekts vinster genom "rören" på sina maskiner. Om vi inte kan fylla röret från en maskin är maskinens avkastning mindre än kostnaden, och minskärningsalgoritmen kommer att hitta det billigare att skära projektets vinstkant istället för maskinens kostnadskant.

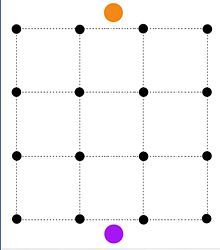
Bildsegmenteringsproblem

Varje svart nod betecknar en pixel.

I bildsegmenteringsproblemet finns det $n$ pixlar. Varje pixel $i$ kan tilldelas ett förgrundsvärde $f i$ eller ett bakgrundsvärde $b i$ . Det finns en straff på $p ij$ om pixlarna $i, j$ ligger intill och har olika tilldelningar. Problemet är att tilldela pixlar till förgrunden eller bakgrunden så att summan av deras värden minus påföljderna är maximal.

Låt $P$ vara den uppsättning pixlar som tilldelats förgrunden och $Q$ vara den uppsättning punkter som tilldelats bakgrunden, då kan problemet formuleras som,

\max\{g\}=\sum _{i\in P}f_{i}+\sum _{i\in Q}b_{i}-\sum _{i\in P,j\in Q\lor j\in P,i\in Q}p_{ij}.

Detta maximeringsproblem kan istället formuleras som ett minimeringsproblem, det vill säga

\min\{g'\}=\sum _{i\in P,j\in Q\lor j\in P,i\in Q}p_{ij}.

Ovanstående minimeringsproblem kan formuleras som ett minimiklipproblem genom att konstruera ett nätverk där källan (orange nod) är ansluten till alla pixlar med kapacitet $f i$ , och sink (lila nod) är ansluten av alla pixlar med kapacitet $b i$ . Två kanter ( $i, j$ ) och ( $j, i$ ) med $p ij$ -kapacitet läggs till mellan två intilliggande pixlar. St cut-set representerar då pixlarna tilldelats förgrunden i $P$ och pixlar tilldelas till bakgrund i $Q$ .

Historia

En redogörelse för upptäckten av satsen gavs av Ford och Fulkerson 1962:

"Bestämning av ett maximalt steady state -flöde från en punkt till en annan i ett nätverk som är föremål för kapacitetsbegränsningar på bågar ... ställde författarna våren 1955 av TE Harris, som tillsammans med general FS Ross (Ret.) hade formulerat en förenklad modell av järnvägstrafikflöde, och pekade ut just detta problem som det centrala som modellen föreslog. Det dröjde inte länge efter att huvudresultatet, sats 5.1, som vi kallar maxflödet min-cut sats, gissades och fastställdes. Ett antal bevis har sedan dykt upp. "

Bevis

Låt $G = (V, E)$ vara ett nätverk (riktad graf) med $s$ och $t$ är källan och sink av $G$ respektive.

Tänk på flödet $f$ beräknat för $G$ av Ford – Fulkerson -algoritmen . I den återstående grafen $($ $G$ $f$ $) som$ erhållits för $G$ (efter den slutliga flödetilldelningen av Ford – Fulkerson -algoritmen ) definierar du två delmängder av hörn enligt följande:

$A$ : uppsättningen hörn som kan nås från $s$ i $G f$
$A c$ : uppsättningen av återstående hörn, dvs $V - A$

Krav. $värde (f) = c (A, A c)$ , där kapaciteten för ett st -snitt definieras av

c(S,T)=\sum \nolimits _{(u,v)\in S\times T}c_{uv}

.

Nu vet vi, för varje delmängd hörn, $A$ . Därför behöver vi för $värde ($ $f$ $) =$ $c$ $($ $A$ $,$ $A$ $c$ $)$ : $value(f)=f_{out}(A)-f_{in}(A)$

Alla utgående kanter från snittet måste vara helt mättade .
Alla inkommande kanter till snittet måste ha nollflöde .

För att bevisa ovanstående påstående överväger vi två fall:

I $G$ finns det en utgående kant så att den inte är mättad, dvs $f$ $($ $x$ $,$ $y$ $) <$ $c$ $xy$ . Detta innebär att det finns en framkant från $x$ till $y$ i $G$ $f$ , därför finns det en väg från $s$ till $y$ i $G$ $f$ , vilket är en motsättning. Därför är utgående kant $($ $x$ $,$ $y$ $)$ helt mättad. $(x,y),x\in A,y\in A^{c}$

I $G$ finns det en inkommande kant så att den bär ett flöde som inte är noll, dvs $f$ $($ $y$ $,$ $x$ $)> 0$ . Detta innebär att det finns en bakåtkant från $x$ till $y$ i $G$ $f$ , därför finns det en väg från $s$ till $y$ i $G$ $f$ , vilket återigen är en motsättning. Därför måste varje inkommande kant $($ $y$ $,$ $x$ $)$ ha nollflöde. $(y,x),x\in A,y\in A^{c}$

Båda ovanstående uttalanden bevisar att kapaciteten för skärning som erhålls på ovan beskrivna sätt är lika med flödet som erhålls i nätet. Flödet erhölls också med Ford-Fulkerson-algoritmen , så det är också nätverkets maxflöde .

Eftersom varje flöde i nätverket alltid är mindre än eller lika med kapaciteten för varje nedskärning som är möjlig i ett nätverk, är ovan beskrivna nedskärning också minskärningen som uppnår maxflödet .

En följd av detta bevis är att det maximala flödet genom en uppsättning kanter i ett snitt i en graf är lika med minimikapaciteten för alla tidigare snitt.

Se även

Referenser

Eugene Lawler (2001). "4.5. Kombinerande implikationer av Max-Flow Min-Cut Theorem, 4.6. Linjär programmeringstolkning av Max-Flow Min-Cut Theorem". Kombinerande optimering: Nätverk och Matroids . Dover. s. 117–120. ISBN 0-486-41453-1.
Christos H. Papadimitriou , Kenneth Steiglitz (1998). "6.1 Maxflödet, Min-Cut-satsen". Kombinerande optimering: algoritmer och komplexitet . Dover. s. 120–128. ISBN 0-486-40258-4.
Vijay V. Vazirani (2004). "12. Introduktion till LP-Duality". Tillnärmningsalgoritmer . Springer. s. 93–100. ISBN 3-540-65367-8.

Languages

In other projects