Pseudoforest - Pseudoforest

En 1-skog (en maximal pseudoforest), bildad av tre 1-träd

Inom grafteori är en pseudoforest en oreglerad graf där varje ansluten komponent har högst en cykel . Det vill säga, det är ett system av hörn och kanter som förbinder par med hörn, så att inga två cykler av på varandra följande kanter delar någon hörn med varandra, och inte heller kan några två cykler anslutas till varandra genom en bana med på varandra följande kanter. Ett pseudoträd är en ansluten pseudoforest.

Namnen är motiverade i analogi med de mer vanligt studerade träd och skogar . (Ett träd är en ansluten graf utan cykler; en skog är en otillbörlig förening av träd.) Gabow och Tarjan tillskriver studien av pseudoforests till Dantzigs bok från 1963 om linjär programmering , där pseudoforests uppstår i lösningen av vissa nätverksflödesproblem . Pseudoforests bildar också grafteoretiska modeller av funktioner och förekommer i flera algoritmiska problem. Pseudoforests är glesa grafer - deras antal kanter är linjärt begränsat när det gäller deras antal hörn (i själva verket har de högst lika många kanter som de har hörn) - och deras matroidstruktur gör att flera andra familjer av glesa grafer kan brytas ned som fackföreningar av skogar och pseudoforest. Namnet "pseudoforest" kommer från Picard & Queyranne (1982) .

Definitioner och struktur

Vi definierar en oriktad graf som en uppsättning hörn och kanter så att varje kant har två hörn (som kan sammanfalla) som slutpunkter. Det vill säga att vi tillåter flera kanter (kanter med samma par slutpunkter) och öglor (kanter vars två slutpunkter är samma hörn). En undergraf av en graf är den graf som bildas av eventuella delmängder av dess hörn och kanter så att varje kant i kantundermängden har båda slutpunkterna i hörnundermängden. En ansluten komponent i en oriktad graf är subgrafen som består av hörn och kanter som kan nås genom att följa kanter från en enda given startpunkt. En graf är ansluten om varje hörn eller kant kan nås från varannan topp eller kant. En cykel i en oriktad graf är en ansluten subgraf där varje toppunkt infaller exakt två kanter, eller är en slinga.

De 21 unicykliska graferna med högst sex hörn

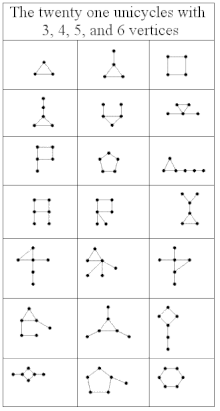
En pseudoforest är en oriktad graf där varje ansluten komponent innehåller högst en cykel. På motsvarande sätt är det en oriktad graf där varje ansluten komponent inte har fler kanter än hörn. Komponenterna som inte har några cykler är bara träd , medan komponenterna som har en enda cykel inom sig kallas 1-träd eller unicykliska grafer . Det vill säga ett 1-träd är en ansluten graf som innehåller exakt en cykel. En pseudoforest med en enda ansluten komponent (kallas vanligtvis ett pseudoträd , även om vissa författare definierar ett pseudoträd som ett 1-träd) är antingen ett träd eller ett 1-träd; i allmänhet kan en pseudoforest ha flera anslutna komponenter så länge de alla är träd eller 1-träd.

Om man tar bort en av kanterna i en cykel från ett 1-träd blir resultatet ett träd. Om man vänder denna process, om man förstärker ett träd genom att ansluta två av dess hörn med en ny kant, blir resultatet ett 1-träd; vägen i trädet som förbinder de två slutpunkterna för den tillagda kanten, tillsammans med den tillagda kanten, bildar 1-trädets unika cykel. Om man förstärker ett 1-träd genom att lägga till en kant som ansluter en av dess hörn till en nyligen tillagd topp, blir resultatet igen ett 1-träd, med ytterligare en toppunkt; en alternativ metod för att bygga 1-träd är att börja med en enda cykel och sedan upprepa denna förstärkningsoperation hur många gånger som helst. Kanterna på alla 1-träd kan delas upp på ett unikt sätt i två undergrafer, varav en är en cykel och den andra är en skog, så att varje träd i skogen innehåller exakt en toppunkt av cykeln.

Vissa mer specifika typer av pseudoforest har också studerats.

En 1-skog , ibland kallad maximal pseudoforest , är en pseudoforest till vilken inga fler kanter kan läggas till utan att någon komponent i grafen innehåller flera cykler. Om en pseudoforest innehåller ett träd som en av dess komponenter kan det inte vara en 1-skog, för man kan lägga till antingen en kant som förbinder två hörn i det trädet, bildar en enda cykel, eller en kant som förbinder det trädet med någon annan komponent. Således är 1-skogarna exakt de pseudoforests där varje komponent är ett 1-träd.

De spänner över pseudoforests av en oriktad graf G är pseudoforest subgrafer av G som har alla hörn av G . En sådan pseudoforest behöver inte ha några kanter, eftersom till exempel undergrafen som har alla hörn av G och inga kanter är en pseudoforest (vars komponenter är träd som består av en enda toppunkt).

De maximala pseudoforests av G är de pseudoforest subgrafer av G som inte finns i någon större pseudoforest av G . En maximal pseudoforest av G är alltid en spännande pseudoforest, men inte omvänt. Om G inte har några anslutna komponenter som är träd, är dess maximala pseudoforests 1-skogar, men om G har en trädkomponent är dess maximala pseudoforests inte 1-skogar. Anges exakt, i någon graf G sina maximala pseudoforests bestå av varje träd komponent i G , tillsammans med en eller flera disjunkta 1-träd som omfattar de återstående hörnen i G .

Regisserade pseudoforests

Versioner av dessa definitioner används också för riktade grafer . Precis som en oriktad graf består en riktad graf av hörn och kanter, men varje kant riktas från en av dess slutpunkter till den andra slutpunkten. En riktad pseudoforest är en riktad graf där varje toppunkt har högst en utgående kant; det vill säga, det har outdegree högst ett. En riktad 1-skog- oftast kallad en funktionell graf (se nedan ), ibland maximalt riktad pseudoforest- är en riktad graf där varje toppunkt har exakt ett. Om D är en riktad pseudoforest är den oriktade grafen som bildas genom att ta bort riktningen från varje kant av D en oriktad pseudoforest.

Antal kanter

Varje pseudoforest på en uppsättning n hörn har högst n kanter, och varje maximal pseudoforest på en uppsättning n hörn har exakt n kanter. Omvänt, om en graf G har egenskapen att, för varje delmängd S av dess hörn, är antalet kanter i den inducerade subgrafen till S högst antalet hörn i S , då är G en pseudoforest. 1-träd kan definieras som anslutna grafer med lika många hörn och kanter.

Om man går från enskilda grafer till graffamiljer, om en familj av grafer har den egenskapen att varje undergraf av en graf i familjen också är i familjen, och varje graf i familjen har högst lika många kanter som hörn, så innehåller familjen bara pseudoforests. Exempelvis är varje subgraf av ett gasreglage (ett diagram ritat så att varje par kanter har en skärningspunkt) också ett spjäll, så Conways gissning om att varje gas har högst så många kanter som hörn kan omarbetas som att varje gas är en pseudoforest. En mer exakt karaktärisering är att om gissningen är sann är spaken exakt pseudoforests utan cykel med fyra vertex och högst en udda cykel.

STREINU och Theran generalisera gleshet villkor definierar pseudoforests: de definierar en kurva som varande ( k , l ) -sparse om varje icke-tom subgraf med n hörn har högst kn  -  l kanter, och ( k , l ) -tight om den är ( k , l ) -sparse och har exakt kn  -  l kanter. Således är pseudoforesterna (1,0) -sparsamma graferna, och de maximala pseudoforesterna är (1,0) -täta graferna. Flera andra viktiga familjer av grafer kan definieras från andra värden på k och l , och när l  ≤  k den ( k , l ) -sparse grafer kan karaktäriseras som graferna utformade som den kant disjunkta unionen av l skogar och k  -  l pseudoforests.

Nästan varje tillräckligt sparsamt slumpmässigt diagram är pseudoforest. Det vill säga, om c är en konstant med 0 < c <1/2, och P _c ( n ) är sannolikheten för att ett jämnt slumpmässigt val bland n -vertexgraferna med cn -kanter resulterar i en pseudoforest, då P _c ( n ) tenderar till en i gränsen för stora n . Men för c > 1/2 har nästan varje slumpmässig graf med cn -kanter en stor komponent som inte är unicyklisk.

Uppräkning

Ett diagram är enkelt om det inte har några självslingor och inga flera kanter med samma slutpunkter. Antalet enkla 1-träd med n märkta hörn är

${\ displaystyle n \ sum _ {k = 1}^{n} {\ frac {(-1)^{k-1}} {k}} \ sum _ {n_ {1} +\ cdots +n_ {k } = n} {\ frac {n!} {n_ {1}! \ cdots n_ {k}!}} {\ binom {{\ binom {n_ {1}} {2}} +\ cdots +{\ binom {n_ {k}} {2}}} {n}}.}$

Värdena för n upp till 300 finns i sekvens OEIS :  A057500 i On-Line Encyclopedia of Integer Sequences .

Antalet maximalt riktade pseudoforest på n hörn, som tillåter självslingor, är n ⁿ , eftersom det för varje toppunkt finns n möjliga slutpunkter för den utgående kanten. André Joyal använde detta faktum för att tillhandahålla ett bijektivt bevis på Cayleys formel , att antalet oriktade träd på n noder är n ^{n  - 2} , genom att hitta en förening mellan maximalt riktade pseudoforest och oriktade träd med två utmärkta noder. Om självslingor inte är tillåtna är antalet maximalt riktade pseudoforests istället ( n-  1) ⁿ .

Diagram över funktioner

En funktion från uppsättningen {0,1,2,3,4,5,6,7,8} till sig själv och motsvarande funktionsdiagram

Riktade pseudoforests och endofunctions är på något sätt matematiskt ekvivalenta. Varje funktion ƒ från en uppsättning X till sig själv (det vill säga en endomorfism av X ) kan tolkas som att den definierar en riktad pseudoforest som har en kant från x till y när ƒ ( x ) = y . Den resulterande riktade pseudoforest är maximal och kan inkludera självslingor när något värde x har ƒ ( x ) = x . Alternativt ger utelämnandet av självslingorna en icke-maximal pseudoforest. I den andra riktningen bestämmer varje maximalt riktad pseudoforest en funktion ƒ så att ƒ ( x ) är målet för kanten som går ut från x , och all icke-maximalt riktad pseudoforest kan göras maximal genom att lägga till självslingor och sedan konvertera till en funktion på samma sätt. Av denna anledning kallas ibland maximalt riktade pseudoforests funktionella grafer . Att se en funktion som en funktionell graf ger ett bekvämt språk för att beskriva egenskaper som inte är lika enkla att beskriva ur funktionsteoretisk synvinkel; denna teknik är särskilt tillämplig på problem med itererade funktioner , som motsvarar vägar i funktionella grafer.

Cykeldetektering , problemet med att följa en väg i ett funktionellt diagram för att hitta en cykel i den, har applikationer inom kryptografi och beräkningstalteori , som en del av Pollards rho -algoritm för heltalsfaktorisering och som en metod för att hitta kollisioner i kryptografiska hashfunktioner . I dessa applikationer förväntas ƒ bete sig slumpmässigt; Flajolet och Odlyzko studerar de grafteoretiska egenskaperna hos de funktionella graferna som härrör från slumpmässigt valda mappningar. I synnerhet innebär en form av födelsedagsparadoxen att i en slumpmässig funktionell graf med n hörn, kommer banan som startar från en slumpmässigt vald topppunkt vanligtvis att gå tillbaka på sig själv för att bilda en cykel inom O ( √ n ) steg. Konyagin et al. har gjort analytiska och beräkningsframsteg med grafstatistik.

Martin, Odlyzko och Wolfram undersöker pseudoforests som modellerar dynamiken i mobilautomater . Dessa funktionella grafer, som de kallar tillståndsövergångsdiagram , har en toppunkt för varje möjlig konfiguration som ensemblen av celler i automaten kan vara i, och en kant som förbinder varje konfiguration med konfigurationen som följer den enligt automatens regel. Man kan utläsa automatens egenskaper från strukturen i dessa diagram, såsom antalet komponenter, begränsningscyklernas längd, trädens djup som förbinder icke-begränsande tillstånd till dessa cykler eller symmetrier i diagrammet. Till exempel motsvarar varje hörn utan inkommande kant ett Edens trädgårdsmönster och en hörn med en självslinga motsvarar ett stillebenmönster .

En annan tidig tillämpning av funktionella grafer är i tågen som används för att studera Steiner trippelsystem . Tåget i ett trippelsystem är en funktionell graf som har en toppunkt för varje möjlig trippel av symboler; varje trippel pqr mappas av ƒ till stu , där pqs , prt och qru är tripplarna som tillhör trippelsystemet och innehåller paren pq , pr respektive qr . Tåg har visat sig vara en kraftfull invariant för trippel system även om det är lite krångligt att beräkna.

Cirkulär matroid

En matroid är en matematisk struktur där vissa uppsättningar element definieras som oberoende , på ett sådant sätt att de oberoende uppsättningarna uppfyller egenskaper som modelleras efter egenskaperna för linjär oberoende i ett vektorutrymme . Ett av standardexemplen på en matroid är den grafiska matroid där de oberoende uppsättningarna är uppsättningarna av kanter i skogar i en graf; skogens matroidstruktur är viktig i algoritmer för att beräkna grafens minsta spänningsträd . Analogt kan vi definiera matroider från pseudoforests.

För varje graf G = ( V , E ) kan vi definiera en matroid på kanterna på G , där en uppsättning kanter är oberoende om och bara om den bildar en pseudoforest; denna matroid är känd som den bicircular matroid (eller cykel matroid ) av G . De minsta beroende uppsättningarna för denna matroid är de minimala anslutna subgraferna av G som har mer än en cykel, och dessa subgrafer kallas ibland cyklar. Det finns tre möjliga typer av cyklar: en theta -graf har två hörn som är anslutna med tre internt sammanhängande banor, en figur 8 -graf består av två cykler som delar en enda hörn, och en handfängningsgraf bildas av två osammanhängande cykler som är anslutna med en väg . En graf är en pseudoforest om och bara om den inte innehåller en cykel som en subgraf.

Förbjudna minderåriga

Den butterfly graf (vänster) och diamantgraf (till höger), förbjudna minderåriga för pseudoforests

Att bilda en minor av en pseudoforest genom att dra ihop några av dess kanter och radera andra producerar en annan pseudoforest. Därför är familjen av pseudoforests stängd under minderåriga, och Robertson -Seymour -satsen innebär att pseudoforests kan karakteriseras i termer av en begränsad uppsättning förbjudna minderåriga , analogt med Wagners sats som karakteriserar de plana graferna som graferna som inte har varken den fullständiga grafen K ₅ eller den fullständiga bipartitdiagrammet K _3,3 som minderåriga. Som diskuterats ovan innehåller varje icke-pseudoforest-graf som en subgraf en handfängsel, figur 8 eller theta-graf; alla handfängsel- eller figur 8-diagram kan vara sammandragna för att bilda en fjärilsgraf (fem-vertex-figur 8), och vilken theta-graf som kan dras ihop för att bilda en diamantgraf (fyra-vertex-theta-graf), så alla icke-pseudoforest innehåller antingen en fjäril eller en diamant som en minor, och dessa är de enda mindre-minimala icke-pseudoforest-graferna. Således är en graf en pseudoforest om och bara om den inte har fjärilen eller diamanten som minor. Om man bara förbjuder diamanten men inte fjärilen, består den resulterande större graffamiljen av kaktusgraferna och sammanfogade föreningar av flera kaktusgrafer.

Mer enkelt, om multigrafer med självslingor övervägs, finns det bara en förbjuden minor, en toppunkt med två slingor.

Algoritmer

En tidig algoritmisk användning av pseudoforests involverar nätverks simplexalgoritmen och dess tillämpning på generaliserade flödesproblem som modellerar omvandlingen mellan varor av olika typer. I dessa problem ges en som inmatning ett flödesnätverk där hörnen modellerar varje vara och kantermodellen tillåter omvandlingar mellan en vara och en annan. Varje kant är markerad med en kapacitet (hur mycket av en vara som kan konverteras per tidsenhet), en flödesmultiplikator (konverteringsfrekvensen mellan varor) och en kostnad (hur mycket förlust eller, om negativ, vinst uppkommer per enhet av omvandling). Uppgiften är att bestämma hur mycket av varje vara som ska konverteras via varje kant i flödesnätet, för att minimera kostnader eller maximera vinsten, samtidigt som man följer kapacitetsbegränsningarna och inte tillåter att varor av någon typ ackumuleras oanvända. Denna typ av problem kan formuleras som ett linjärt program och lösas med hjälp av simplexalgoritmen . De mellanliggande lösningarna som härrör från denna algoritm, liksom den eventuella optimala lösningen, har en speciell struktur: varje kant i ingångsnätet är antingen oanvänd eller används till sin fulla kapacitet, förutom en delmängd av kanterna, som bildar en spännande pseudoforest av ingångsnätet, för vilket flödesmängderna kan ligga mellan noll och full kapacitet. I denna ansökan kallas unicykliska grafer ibland också förstärkta träd och maximala pseudoforest kallas också ibland förstorade skogar .

Den minsta spänner pseudoforest problem handlar om att hitta en som spänner över pseudoforest av minimal vikt i en större kant-viktad graf G . På grund av pseudoforests matroidstruktur kan maximala pseudoforests med minimal vikt hittas av giriga algoritmer som liknar dem för det minimala spanträdsproblemet . Gabow och Tarjan fann dock en mer effektiv linjär tidsmetod i detta fall.

Den pseudoarboricity av en graf G definieras genom analogi med arboricity som det minsta antal pseudoforests in i vilken dess kanter kan partitione; ekvivalent är det minsta k så att G är ( k , 0) -gles, eller minimum k så att kanterna på G kan orienteras för att bilda en riktad graf med högst k grader . På grund av pseudoforests matroidstruktur kan pseudoarboriciteten beräknas under polynomtid.

En slumpmässig bipartitgraf med n hörn på vardera sidan av sin tvådelning, och med cn -kanter valda oberoende slumpmässigt från var och en av de n ² möjliga paren hörn, är en pseudoforest med hög sannolikhet när c är en konstant strikt mindre än en. Detta faktum spelar en nyckelroll i analysen av gökhashning , en datastruktur för att leta upp nyckel-värdepar genom att titta i en av två hashtabeller på platser som bestäms från nyckeln: man kan bilda en graf, "gökgrafen", vars hörn motsvarar hashtabellplatser och vars kanter länkar de två platser där en av nycklarna kan hittas, och gökhashalgoritmen lyckas hitta platser för alla dess nycklar om och bara om gökgrafen är en pseudoforest.

Pseudoforests spelar också en nyckelroll i parallella algoritmer för graffärgning och relaterade problem.

Anteckningar

Referenser

externa länkar

• Weisstein, Eric W. , "Unicyclic Graph" , MathWorld