Kvanttillstånd som är ett element i ett Fock-utrymme med ett väldefinierat antal partiklar (eller kvanta)
I kvantmekanik är ett Fock-tillstånd eller taltillstånd ett kvanttillstånd som är ett element i ett Fock-utrymme med ett väldefinierat antal partiklar (eller kvantor ). Dessa stater är uppkallade efter den sovjetiska fysikern Vladimir Fock . Fock-stater spelar en viktig roll i den andra kvantiseringsformuleringen av kvantmekanik.
Partikelrepresentationen behandlades först i detalj av Paul Dirac för bosoner och av Pascual Jordan och Eugene Wigner för fermioner . Fock-staterna bosoner och fermioner följer användbara relationer med avseende på Focks rymdskapande och förintelseoperatörer .
Definition
Man specificerar ett multipartikeltillstånd av N icke-interagerande identiska partiklar genom att skriva tillståndet som en summa av tensorprodukter av N enpartikeltillstånd. Dessutom, beroende på fullständighet av partiklarnas spinn måste tensorprodukter vara alternerande (anti-symmetriska) eller symmetriska produkter av den underliggande one-partikel Hilbert space . Specifikt:
-
Fermioner , som har ett halvt heltal snurr och följer Pauli-uteslutningsprincipen , motsvarar antisymmetriska tensorprodukter.
-
Bosoner som har heltalssnurr (och inte regleras av uteslutningsprincipen) motsvarar symmetriska tensorprodukter.
Om antalet partiklar är variabelt konstruerar man Fock-utrymmet som den direkta summan av tensorprodukten som Hilbert rymmer för varje partikelnummer . I Fock-utrymmet är det möjligt att specificera samma tillstånd i en ny notation, beläggningsnummernotationen, genom att ange antalet partiklar i varje möjligt enpartikel-tillstånd.
Låta vara en ortonormal grund för tillstånd i det underliggande Hilbert-rummet med en partikel. Detta inducerar en motsvarande bas för Fock-utrymmet som kallas "beläggningsnummerbas". Ett kvanttillstånd i Fock-utrymmet kallas ett Fock-tillstånd om det är en del av beläggningsnummerbasen.

En Fock state uppfyller ett viktigt kriterium: för varje i , är tillståndet en eigenstate av partikelantal operatören motsvarande den i : te elementära tillstånd k i . Motsvarande egenvärde ger antalet partiklar i tillståndet. Detta kriterium definierar nästan Fock-tillstånden (man måste dessutom välja en fasfaktor).

Ett givet Fock-tillstånd betecknas med . I detta uttryck betecknar antalet partiklar i den i: te tillståndet k i , och partikelantals operatör för det i: te tillståndet, , verkar på Fock tillståndet på följande sätt:




Därför är Fock-tillståndet en egenstat för nummeroperatören med egenvärde .

Fock-stater utgör ofta den mest bekväma grunden för ett Fock-utrymme. Element i ett Fock-utrymme som är överlagringar av tillstånd med olika partikelnummer (och därmed inte egenstatus för nummeroperatören) är inte Fock-tillstånd. Av denna anledning kallas inte alla element i ett Fock-utrymme som "Fock-tillstånd".
Om vi definierar den samlade partikelnummeroperatören som


definitionen av Fock statliga säkerställer att variansen av mätningen , dvs mätning av antalet partiklar i ett Fock tillstånd alltid returnerar ett bestämt värde utan någon fluktuation.

Exempel på användning av två partiklar
För alla slutliga tillstånd , alla Fock-tillstånd av två identiska partiklar som ges av , och alla operatörer , har vi följande villkor för oskiljbarhet :



-
 .
.
Så vi måste ha 
var för bosoner och för fermioner . Eftersom och är godtyckliga kan vi säga,




-
 för bosoner och
för bosoner och
-
 för fermioner.
för fermioner.
Observera att nummeroperatören inte skiljer bosoner från fermioner; det räknar faktiskt bara partiklar utan hänsyn till deras symmetrityp. För att uppfatta någon skillnad mellan dem behöver vi andra operatörer, nämligen skapande och förintelse .
Bosonic Fock-stat
Bosoner , som är partiklar med heltalssnurr, följer en enkel regel: deras sammansatta egenstat är symmetrisk under drift av en växeloperatör . Till exempel i ett tvåpartikelsystem i tensorproduktrepresentationen vi har .

Boson skapande och förintelse operatörer
Vi borde kunna uttrycka samma symmetriska egenskap i denna nya Fock-rymdrepresentation. För detta har vi införa icke-Hermitska bosoniska skapande och förintelseoperatorer , betecknas av och respektive. Dessa operatörers agerande på ett Fock-tillstånd ges av följande två ekvationer:


- Skapningsoperatör :


- Annihilation operatör :


Icke-eremiticitet hos skapare och förintelseoperatörer
Bosonic Focks tillståndsskapande och förintelseoperatörer är inte Hermitiska operatörer .
| Bevis för att skapande och förintelse operatörer inte är Hermitian.
|
För ett Fock-tillstånd ,
 ![{\ displaystyle {\ begin {align} \ left \ langle n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3} } ... n _ {\ mathbf {k} _ {l}} - 1, ... \ left | b _ {\ mathbf {k} _ {l}} \ right | n _ {\ mathbf {k} _ {1 }}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf {k} _ {l}}, ... \ right \ rangle & = {\ sqrt {n _ {\ mathbf {k} _ {l}}}} \ left \ langle n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}} , n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf {k} _ {l}} - 1, ... | n _ {\ mathbf {k} _ {1}}, n_ { \ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf {k} _ {l}} - 1, ... \ höger \ rangle \\ [6pt] \ left (\ left \ langle n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} .. .n _ {\ mathbf {k} _ {l}}, ... \ left | b _ {\ mathbf {k} _ {l}} \ right | n _ {\ mathbf {k} _ {1}}, n_ { \ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf {k} _ {l}} - 1, ... \ right \ rangle \ right ) ^ {*} & = \ left \ langle n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}}. ..n _ {\ mathbf {k} _ {l}} - 1 ... \ left | b _ {\ mathbf {k} _ {l}} ^ {\ dolk} \ right | n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathb f {k} _ {l}}, ... \ höger \ rangle \\ & = {\ sqrt {n _ {\ mathbf {k} _ {l}} + 1}} \ vänster \ langle n _ {\ mathbf { k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf {k} _ {l}} - 1 ... | n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf { k} _ {l}} + 1 ... \ höger \ rangle \ slut {justerad}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bae70fd2029e80decb9fed2998f2ae5288c81577)
Därför är det uppenbart att anslutning till skapande (förintelse) operatör inte går in i sig själv. Därför är de inte Hermitian-operatörer.
Men anslutning till skapande (förintelse) operatör är förintelse (skapande) operatör.
|
Operatörens identiteter
Kommuteringsförhållandena mellan skapare och förintelseoperatörer i ett bosoniskt system är
![{\ displaystyle \ left [b_ {i} ^ {\,}, b_ {j} ^ {\ dolk} \ höger] \ equiv b_ {i} ^ {\,} b_ {j} ^ {\ dolk} -b_ {j} ^ {\ dolk} b_ {i} ^ {\,} = \ delta _ {ij},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00094b3ba3092d2da457b3c7d7907a5b51634f5d)
![{\ displaystyle \ left [b_ {i} ^ {\ dolk}, b_ {j} ^ {\ dolk} \ höger] = \ vänster [b_ {i} ^ {\,}, b_ {j} ^ {\, } \ right] = 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77c29a498d3ddcbc046b29519e1cee9b2f0e5a1c)
var är kommutatorn och är Kronecker-deltaet .
![[\ \, \ \]](https://wikimedia.org/api/rest_v1/media/math/render/svg/53965cb2f0bcd587b309dad04b1fed4736a0d2ea)

N bosonisk grundtillstånd 
| Antal partiklar (N)
|
Bosonisk grund säger
|
| 0 |

|
| 1 |
 , , , ... , , , ...
  |
| 2 |
 , , , ... , , , ...
  |
| ... |
...
|
Åtgärd mot vissa specifika Fock-stater
- För ett vakuumtillstånd - ingen partikel är i något tillstånd - uttryckt som , har vi:


och . Det vill säga den l : te operatören skapande skapar en partikel i l : te tillståndet k l , och vakuumtillståndet är en fast punkt i förintelseoperatorer som det finns inga partiklar att förinta.
- Vi kan generera vilket Fock-tillstånd som helst genom att arbeta på vakuumtillståndet med ett lämpligt antal skapande operatörer :

- För ett enskilt läge Fock-tillstånd, uttryckt som ,,

-
 och,
och,

Antal operatörer
Nummeroperatorerna för ett bosoniskt system ges av , var


Nummeroperatörer är Hermitian-operatörer.
Symmetriskt beteende hos bosonic Fock-tillstånd
Pendlingsförhållandena mellan skapande- och förintelsearperatorerna säkerställer att de bosoniska Fock-staterna har lämpligt symmetriskt beteende under partikelutbyte. Här sker utbyte av partiklar mellan två tillstånd (säg l och m ) genom att utplåna en partikel i tillstånd l och skapa en i tillstånd m . Om vi börjar med ett Fock-tillstånd och vill flytta en partikel från tillstånd till tillstånd , så arbetar vi Fock-tillståndet på följande sätt:




Med hjälp av kommuteringsrelationen vi har, 

Så, Bosonic Fock-staten beter sig symmetriskt under drift av Exchange-operatören.
Wigner funktion av 
Wigner funktion av 
Wigner funktion av 
Wigner funktion av 
Wigner funktion av 
Fermioniskt Fock-tillstånd
Fermion skapande och förintelse operatörer
För att kunna behålla fermionernas antisymmetriska beteende introducerar vi för Fermionic Fock-tillstånd icke-Hermitiska fermionskapande och förintelseoperatorer, definierade för ett Fermionic Fock-tillstånd som:

- Den operatör skapa fungerar som:


- Den förintelse Operatören fungerar som:


Dessa två åtgärder görs antisymmetriskt, vilket vi kommer att diskutera senare.
Operatörens identiteter
Antikommutationsförhållandena mellan skapande och förintelse av operatörer i ett fermioniskt system är,
-

var är antikommutatorn och är Kronecker-deltaet . Dessa antikommutationsförhållanden kan användas för att visa antisymmetriskt beteende hos Fermionic Fock-tillstånd .


Antal operatörer
Nummeroperatörer för Fermions ges av .



Maximal yrkesantal
Nummeroperatörens handlingar såväl som skapande och förintelseoperatörer kan verka samma som de bosoniska, men den verkliga vridningen kommer från det maximala ockupationsantalet för varje stat i det fermioniska Fock-tillståndet. Genom att utvidga det 2-partikelformade fermioniska exemplet ovan, måste vi först övertyga oss om att ett fermioniskt Fock-tillstånd erhålls genom att tillämpa en viss summa av permutationsoperatorer på tensorprodukten av egenkit enligt följande:


Denna determinant kallas Slater-determinanten . Om något av de enskilda partikeltillstånden är desamma, skulle två rader av Slater-determinanten vara desamma och följaktligen skulle determinanten vara noll. Därför får två identiska fermioner inte uppta samma tillstånd (ett uttalande av Pauli-uteslutningsprincipen ). Därför är ockupationsnumret för varje enskilt tillstånd antingen 0 eller 1. Egenvärdet associerat med det fermioniska Fock-tillståndet måste vara antingen 0 eller 1.

N fermionisk grundtillstånd 
| Antal partiklar (N) |
Fermionisk grundtillstånd
|
| 0 |

|
| 1 |
 , , , ... , , , ...
  |
| 2 |
 , , , ... , , , ...
   |
| ... |
...
|
Åtgärd mot vissa specifika Fock-stater
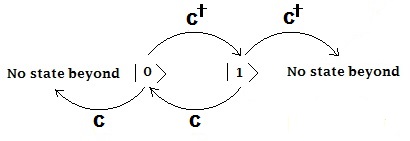
- För ett fermoniskt Fock-tillstånd i ett läge, uttryckt som ,


och eftersom det maximala ockupationsantalet för varje stat är 1. Inte mer än 1 fermion kan ockupera samma tillstånd, som anges i Pauli-uteslutningsprincipen .
- För ett fermoniskt Fock-tillstånd i ett läge, uttryckt som ,


och eftersom partikelantalet inte kan vara mindre än noll.
- För ett multimode fermioniskt Fock-tillstånd, uttryckt som,

-
 ,
,
där kallas Jordan-Wigner-strängen , som beror på ordningen av de involverade enpartikelstaterna och att lägga till fermions ockupationsnummer för alla föregående stater.
Antisymmetriskt beteende av Fermionic Fock-tillstånd
Antisymmetriskt beteende hos Fermionic-stater under Exchange-operatören tas hand om anticommutation-förhållandena. Här görs utbyte av partiklar mellan två tillstånd genom att utplåna en partikel i ett tillstånd och skapa en i en annan. Om vi börjar med ett Fock-tillstånd och vill skifta en partikel från tillstånd till tillstånd , så använder vi Fock-tillståndet på följande sätt:




Använda förhållandet mot kommutation vi har


men,

Således är fermioniska Fock-tillstånd antisymmetriska under drift av partikelutbytesoperatörer.
Fock-tillstånd är inte energi-egenstater i allmänhet
I den andra kvantiseringsteorin ges den Hamiltoniska densitetsfunktionen av

Den totala Hamiltonian ges av

I fri Schrödinger-teori,

och

och
-
 ,
,
var är utrotningsoperatören.


Endast för icke-interagerande partiklar gör och pendlar; i allmänhet pendlar de inte. För icke-interagerande partiklar,



Om de inte pendlar kommer Hamiltonian inte att ha ovanstående uttryck. Därför är Fock-tillstånd i allmänhet inte energistyrstatus i ett system.
Vakuumfluktuationer
Vakuumtillståndet eller är tillståndet med lägsta energi och förväntningsvärdena för och försvinner i detta tillstånd:




De elektriska och magnetiska fälten och vektorpotentialen har lägeutvidgningen av samma allmänna form:

Således är det lätt att se att förväntningsvärdena för dessa fältoperatörer försvinner i vakuumtillstånd:

Det kan dock visas att förväntningsvärdena för kvadraten för dessa fältoperatörer är icke-noll. Det finns alltså fluktuationer i fältet om nollensemble-genomsnittet. Dessa vakuumfluktuationer är ansvariga för många intressanta fenomen, inklusive lammförskjutningen i kvantoptik.
Multi-mode Fock-tillstånd
I ett fält med flera lägen arbetar varje skapande- och förintelseoperatör på sitt eget läge. Så och kommer bara att fungera . Eftersom operatörer som motsvarar olika lägen arbetar i olika delutrymmen i Hilbert-utrymmet är hela fältet en direkt produkt av över alla lägen:





Skapande- och förintelseoperatörerna arbetar i multilägetillståndet genom att bara höja eller sänka nummertillståndet för sitt eget läge:

Vi definierar också det totala antalet operatörer för fältet som är en summa av antalet operatörer för varje läge:

Multiläget Fock-tillstånd är en egenvektor för totalantaloperatören vars egenvärde är det totala ockupationsnumret för alla lägen

Vid partiklar som inte samverkar, pendlar nummeroperatören och Hamiltonian varandra och följaktligen blir Fock-tillstånd i flera lägen egenstatus för Hamilton-multiläget

Källa till enstaka foton tillstånd
Enstaka fotoner genereras rutinmässigt med hjälp av enstaka sändare (atomer, kväve-vakanscentrum , kvantpunkt ). Dessa källor är emellertid inte alltid så effektiva, vilket ofta ger låg sannolikhet att faktiskt få en enda foton på begäran; och ofta komplexa och olämpliga ur en laboratoriemiljö.
Andra källor används ofta för att övervinna dessa problem på bekostnad av ett icke-bestämt beteende. Heralded enskilda fotonkällor är probabilistiska tvåfotonkällor från vilka paret delas och detekteringen av en foton förkunnar närvaron av den återstående. Dessa källor förlitar vanligtvis på den optiska icke-linjariteten hos vissa material gillar periodiskt polad Litiumniobat ( Spontan parametrisk nedkonvertering ) eller kisel (spontan fyrvågsblandning ) till exempel.
Icke-klassiskt beteende
Den Glauber-Sudarshan P-representation av Fock påstår visar att dessa tillstånd är rent kvantmekaniska och har ingen klassisk motsvarighet. Den av dessa stater i representationen är en ': te derivatan av deltafunktion Dirac och därför inte en klassisk sannolikhetsfördelning.


Se även
Referenser
externa länkar






























![{\ displaystyle {\ begin {align} \ left \ langle n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3} } ... n _ {\ mathbf {k} _ {l}} - 1, ... \ left | b _ {\ mathbf {k} _ {l}} \ right | n _ {\ mathbf {k} _ {1 }}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf {k} _ {l}}, ... \ right \ rangle & = {\ sqrt {n _ {\ mathbf {k} _ {l}}}} \ left \ langle n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}} , n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf {k} _ {l}} - 1, ... | n _ {\ mathbf {k} _ {1}}, n_ { \ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf {k} _ {l}} - 1, ... \ höger \ rangle \\ [6pt] \ left (\ left \ langle n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} .. .n _ {\ mathbf {k} _ {l}}, ... \ left | b _ {\ mathbf {k} _ {l}} \ right | n _ {\ mathbf {k} _ {1}}, n_ { \ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf {k} _ {l}} - 1, ... \ right \ rangle \ right ) ^ {*} & = \ left \ langle n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}}. ..n _ {\ mathbf {k} _ {l}} - 1 ... \ left | b _ {\ mathbf {k} _ {l}} ^ {\ dolk} \ right | n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathb f {k} _ {l}}, ... \ höger \ rangle \\ & = {\ sqrt {n _ {\ mathbf {k} _ {l}} + 1}} \ vänster \ langle n _ {\ mathbf { k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf {k} _ {l}} - 1 ... | n _ {\ mathbf {k} _ {1}}, n _ {\ mathbf {k} _ {2}}, n _ {\ mathbf {k} _ {3}} ... n _ {\ mathbf { k} _ {l}} + 1 ... \ höger \ rangle \ slut {justerad}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bae70fd2029e80decb9fed2998f2ae5288c81577)
![{\ displaystyle \ left [b_ {i} ^ {\,}, b_ {j} ^ {\ dolk} \ höger] \ equiv b_ {i} ^ {\,} b_ {j} ^ {\ dolk} -b_ {j} ^ {\ dolk} b_ {i} ^ {\,} = \ delta _ {ij},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00094b3ba3092d2da457b3c7d7907a5b51634f5d)
![{\ displaystyle \ left [b_ {i} ^ {\ dolk}, b_ {j} ^ {\ dolk} \ höger] = \ vänster [b_ {i} ^ {\,}, b_ {j} ^ {\, } \ right] = 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77c29a498d3ddcbc046b29519e1cee9b2f0e5a1c)
![[\ \, \ \]](https://wikimedia.org/api/rest_v1/media/math/render/svg/53965cb2f0bcd587b309dad04b1fed4736a0d2ea)