Teori om algebraisk graf - Algebraic graph theory

En mycket symmetrisk graf, Petersen-grafen , som är vertex-transitiv , symmetrisk , distans-transitiv och distansregelbunden . Den har diameter 2. Dess automorfismgrupp har 120 element och är i själva verket den symmetriska gruppen . ${\ displaystyle S_ {5}}$

Algebraisk grafteori är en gren av matematik där algebraiska metoder tillämpas på problem med diagram . Detta står i kontrast till geometriska , kombinatoriska eller algoritmiska tillvägagångssätt. Det finns tre huvudgrenar för algebraisk grafteori, som involverar användningen av linjär algebra , användningen av gruppteori och studien av grafinvarierare .

Grenar av algebraisk grafteori

Använda linjär algebra

Den första grenen av algebraisk grafteori involverar studier av grafer i samband med linjär algebra . Speciellt studerar den spektrumet för angränsningsmatrisen eller den laplaciska matrisen i en graf (denna del av algebraisk grafteori kallas också spektralgrafteori ). För Petersen-diagrammet är till exempel spektrumet för angränsningsmatrisen (−2, −2, −2, −2, 1, 1, 1, 1, 1, 3). Flera satser relaterar spektrumets egenskaper till andra grafegenskaper . Som ett enkelt exempel kommer en ansluten graf med diametern D att ha åtminstone D +1 distinkta värden i sitt spektrum. Aspekter av grafspektra har använts för att analysera synkroniserbarheten för nätverk .

Använda gruppteori

Den andra grenen av algebraisk grafteori involverar studier av grafer i samband med gruppteori , särskilt automorfismgrupper och geometrisk gruppteori . Fokus läggs på olika familjer av grafer baserade på symmetri (såsom symmetriska grafer , vertex-transitiva grafer , kanttransitiva grafer , distans-transitiva grafer , distansregelbundna grafer och starkt regelbundna grafer ) och på inkluderingsförhållandena mellan dessa familjer. Vissa av sådana kategorier av grafer är tillräckligt glesa för att listor över grafer kan upprättas. Genom Fruchts teorem kan alla grupper representeras som automorfismgruppen i en ansluten graf (i själva verket en kubisk graf ). En annan koppling till gruppteorin är att, med tanke på vilken grupp som helst, kan symmetriska diagram som kallas Cayley-grafer genereras, och dessa har egenskaper relaterade till gruppens struktur.

En Cayley graf för alternerande gruppen A ₄ , som bildar en stympad tetraeder i tre dimensioner. Alla Cayley-grafer är vertex-transitive , men vissa vertex-transitive grafer (som Petersen-diagrammet ) är inte Cayley-grafer.

En korrekt toppfärgning av Petersen-grafen med 3 färger, det minsta möjliga antalet. Enligt det kromatiska polynomet finns det 120 sådana färgämnen med 3 färger.

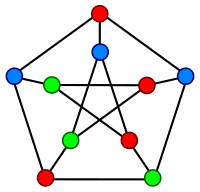
Denna andra gren av algebraisk grafteori är relaterad till den första, eftersom symmetriegenskaperna för en graf återspeglas i dess spektrum. Speciellt har spektrumet för en högsymmetrisk graf, såsom Petersen-grafen, få distinkta värden (Petersen-diagrammet har 3, vilket är det minsta möjliga med tanke på dess diameter). För Cayley-grafer kan spektrumet relateras direkt till gruppens struktur, särskilt till dess oreducerbara tecken .

Studerar diagraminvarianter

Slutligen gäller den tredje grenen av algebraisk grafteori algebraiska egenskaper hos invarianter av grafer, och särskilt de kromatiska polynomierna , Tutte-polynom- och knutinvarierarna . Det kromatiska polynomet i en graf räknar till exempel antalet rätta toppfärgningar . För Petersen-grafen är detta polynom . Detta innebär i synnerhet att Petersen-grafen inte kan färgas ordentligt med en eller två färger utan kan färgas på 120 olika sätt med 3 färger. Mycket arbete inom detta område med algebraisk teori motiverades av försök att bevisa fyrfärgssatsen . Det finns emellertid fortfarande många öppna problem , som att karakterisera grafer som har samma kromatiska polynom och bestämma vilka polynom som är kromatiska. ${\ displaystyle t (t-1) (t-2) (t ^ {7} -12t ^ {6} + 67t ^ {5} -230t ^ {4} + 529t ^ {3} -814t ^ {2} + 775t-352)}$

Se även

• Teori om spektralgraf
• Algebraisk kombinatorik
• Algebraisk anslutning
• Dulmage – Mendelsohn nedbrytning
• Grafegenskap
• Adjacency matris

Referenser

externa länkar

• Media relaterade till algebraisk grafteori på Wikimedia Commons