Median väljar sats - Median voter theorem

Den medianväljarteorin är en proposition rörande rankad preferens röstning som lagts fram av Duncan Black 1948. Det sägs att om väljarna och politik är fördelade längs en endimensionell spektrum , med väljarna ranking alternativ för närhets, sedan någon omröstning metod som uppfyller Condorcet -kriteriet väljer den kandidat som ligger närmast medianväljaren. Framför allt kommer en majoritet mellan två alternativ att göra det.

Satsen är förknippad med valfrihetsekonomi och statistisk statsvetenskap . Partha Dasgupta och Eric Maskin har hävdat att det ger en kraftfull motivering för röstmetoder baserade på Condorcet -kriteriet. Plots majoritetsregel jämviktssats sträcker sig till två dimensioner.

Ett löst besläktat påstående hade gjorts tidigare (1929) av Harold Hotelling . Det är inte en sann sats och mer korrekt kallas medianväljaren teori eller median väljare modell . Den säger att i en representativ demokrati kommer politikerna att konvergera till medianväljarens synvinkel.

Uttalande och bevis på satsen

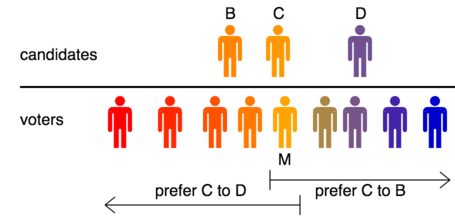
Kandidat C   är närmast medianväljaren M .

Antag att det finns ett udda antal väljare och minst två kandidater, och anta att åsikter fördelas längs ett spektrum. Antag att varje väljare rankar kandidaterna i en ordning av närhet så att kandidaten närmast väljaren får sin första preferens, nästa närmaste får sin andra preferens och så vidare. Sedan finns det en medianväljare och vi kommer att visa att valet kommer att vinnas av den kandidat som står honom eller henne närmast.

Bevis . Låt medianväljaren vara Marlene. Den kandidat som står henne närmast får sin första preferensröst. Antag att den här kandidaten är Charles och att han ljuger till vänster om henne. Sedan kommer Marlene och alla väljare till vänster (som består av en majoritet av väljarna) att föredra Charles framför alla kandidater till hans högra, och Marlene och alla väljare till hennes höger kommer att föredra Charles framför alla kandidater till sin vänster.

Condorcet -kriteriet definieras som uppfyllt av alla röstmetoder som säkerställer att en kandidat som föredras framför alla andra kandidater av en majoritet av väljarna kommer att bli vinnaren, och detta är just fallet med Charles här; så det följer att Charles kommer att vinna val som genomförs med en metod som uppfyller Condorcet -kriteriet.

Under varje röstmetod som uppfyller Condorcet -kriteriet kommer vinnaren därför att vara den kandidat som föredras av medianväljaren. För binära beslut uppfyller majoriteten av rösterna kriteriet; för flervägsröster uppfyller flera metoder det (se Condorcet -metoden ).

Antaganden

Satsen gäller också när antalet väljare är jämnt, men detaljerna beror på hur band löses.

Antagandet att preferenser är gjorda i närheten av närhet kan avslappnas för att bara säga att de är enstaka .

Antagandet att åsikter ligger längs en verklig linje kan slappna av för att tillåta mer allmänna topologier.

Historia

Satsen fastställdes först av Duncan Black 1948. Han skrev att han såg ett stort glapp i ekonomisk teori om hur omröstning avgör resultatet av beslut, inklusive politiska beslut. Blacks papper utlöste forskning om hur ekonomi kan förklara röstsystem. År 1957 redogjorde Anthony Downs för medianväljarens sats i sin bok An Economic Theory of Democracy .

Tillägg till distributioner i mer än en dimension

Medianväljarens sats i två dimensioner

Medianväljarens sats gäller i begränsad form för fördelningar av väljares åsikter i utrymmen av vilken dimension som helst. En fördelning i mer än en dimension behöver inte nödvändigtvis ha en median i alla riktningar (som kan kallas en "allriktad median"); Men en bred klass av rotationssymmetriska distributioner, inklusive Gauss , inte har en median av detta slag. När fördelningen av väljare har en unik median i alla riktningar och väljarna rankar kandidater i närheten av närhet, gäller medianväljarens sats: kandidaten närmast medianen kommer att ha majoritetspreferens framför alla sina rivaler, och kommer att väljas av valfri röstmetod som uppfyller Condorcet -kriteriet. (Unikhet här generaliserar egenskapen som garanteras av konstigheten i urvalet i en enda dimension.)

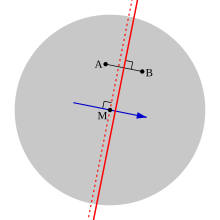
Bevis . Se diagrammet där den grå skivan representerar väljarfördelningen som enhetlig över en cirkel och M är medianen i alla riktningar. Låt A och B vara två kandidater, av vilka A är närmare medianen. Då är väljarna som rankar A över B precis de till vänster (dvs "A" -sidan) av den solida röda linjen; och eftersom A är närmare än B till M, är medianen också till vänster om denna rad.

En fördelning utan median i alla riktningar

Nu, eftersom M är en median i alla riktningar, sammanfaller den med den endimensionella medianen i det specifika fallet av riktningen som visas med den blå pilen, som är vinkelrät mot den heldragna röda linjen. Således, om vi drar en röd streckad linje genom M, vinkelrätt mot den blå pilen, kan vi säga att hälften av väljarna ligger till vänster om denna rad. Men eftersom denna rad i sig är till vänster om den solida röda linjen följer det att mer än hälften av väljarna kommer att rankas A över B.

Det är lätt att konstruera väljarfördelningar som inte har en median i alla riktningar. Det enklaste exemplet består av en fördelning begränsad till 3 punkter som inte ligger i en rak linje, till exempel 1, 2 och 3 i det andra diagrammet. Varje väljarplats sammanfaller med medianen under en viss uppsättning endimensionella projektioner. Om A, B och C är kandidaterna kommer "1" att rösta ABC, "2" rösta BCA och "3" rösta CAB, vilket ger en Condorcet -cykel. Detta är ämnet för McKelvey – Schofield -satsen .

Förhållandet mellan medianen i alla riktningar och den geometriska medianen

Närhelst en unik allriktad median finns, bestämmer den resultatet av Condorcets omröstningsmetoder. Samtidigt kan den geometriska medianen identifieras som den idealiska vinnaren av ett rankat preferensval (se Jämförelse av valsystem ). Det är därför viktigt att känna till förhållandet mellan de två. Faktum är att när en median i alla riktningar existerar (åtminstone för diskreta fördelningar) sammanfaller den med den geometriska medianen.

Diagram för lemma

Lemma . När en diskret distribution har en median M   i alla riktningar  måstedatapunkterna som inte finns vid M komma i balanserade par ( A , A  ') på vardera sidan av M   med egenskapen att A  -  M  -  A  ' är en rak linje ( dvs. inte som A  0  -  M  -  A  2 i diagrammet).

Bevis . Detta resultat bevisades algebraiskt av Charles Plott 1967. Här ger vi ett enkelt geometriskt bevis genom motsägelse i två dimensioner.

Antag tvärtom att det finns en uppsättning punkter A i som har M   som median i alla riktningar, men för vilka punkterna som inte sammanfaller med M   inte kommer i balanserade par. Då kan vi ta bort från denna uppsättning alla punkter vid M och alla balanserade par om M , utan att M   slutar att vara en median i någon riktning; så M   förblir en allriktad median.

Om antalet återstående poäng är udda kan vi enkelt dra en linje genom M   så att majoriteten av punkterna ligger på ena sidan av den, vilket motsäger M -medianegenskapen .

Om talet är jämnt, säg 2 n , då kan vi märka punkterna A  0 , A 1 , ... i medurs ordning om att M   börjar när som helst (se diagrammet). Låt θ vara vinkeln som böjas av M  - A  0 till M  - A n . Om θ <180 ° som visas kan vi sedan rita en linje som liknar den brutna röda linjen genom M   som har de flesta datapunkterna på ena sidan av den, vilket igen motsäger medianegenskapen för M  ; medan om θ> 180 ° gäller samma sak med de flesta punkterna på andra sidan. Och om θ = 180 °, då bildar A  0 och A n ett balanserat par, som motsäger ett annat antagande.    

Sats . När en diskret fördelning har en median M   i alla riktningar sammanfaller den med dess geometriska median.

Bevis . Summan av avstånd från valfri punkt P   till en uppsättning datapunkter i balanserade par ( A , A  ') är summan av längderna A  -  P  -  A  '. Varje individuell längd denna form minimeras över P   när linjen är rak, såsom händer när P   sammanfaller med M . Summan av avstånd från P   till eventuella datapunkter belägna vid M   minimeras på samma sätt när P   och M   sammanfaller. Sålunda summan av avstånden från datapunkter till P   minimeras när P   sammanfaller med M  .

Hotellings lag

Ju mer informella påstående - medianväljarmodellen - är relaterad till Harold Hotelling s 'principen om minimal differentiering', även känd som ' Hotel lag '. Den säger att politiker drar sig mot den position som medianväljaren intar, eller mer allmänt mot den position som valsystemet gynnar. Det lades första gången fram (som en observation, utan krav på stränghet) av Hotelling 1929.

Hotelling såg politikernas beteende med en ekonomes ögon. Han slogs av det faktum att butiker som säljer en viss vara ofta samlas i samma del av en stad och såg detta som analogt konvergens mellan politiska partier. I båda fallen kan det vara en rationell politik för att maximera marknadsandelar .

Som med alla karaktäriseringar av mänsklig motivation beror det på psykologiska faktorer som inte är lätt att förutsäga och som omfattas av många undantag. Det är också beroende av röstningssystemet: politiker kommer inte att konvergera till medianväljaren om inte valprocessen gör det. Om en valprocess ger större vikt åt landsbygden än till stadsväljare, kommer partierna sannolikt att konvergera till politik som gynnar landsbygden snarare än till den sanna medianen.

Användningar av medianväljarens sats

Satsen är värdefull för det ljus som den kastar på optimiteten (och gränserna för optimaliteten) för vissa röstsystem.

Valerio Dotti påpekar bredare tillämpningsområden:

Den medianväljarteorin visat sig vara mycket populär i politisk ekonomi litteratur. Huvudskälet är att det kan antas för att härleda testbara konsekvenser om förhållandet mellan vissa egenskaper hos den röstande befolkningen och det politiska resultatet, abstrahera från andra drag i den politiska processen.

Han tillägger att ...

Medianväljarresultatet har tillämpats på en otrolig mängd frågor. Exempel är analysen av förhållandet mellan inkomstskillnader och storleken på statliga ingripanden i omfördelningspolitiken (Meltzer och Richard, 1981), studien av bestämmelserna för invandringspolitiken (Razin och Sadka, 1999), av omfattningen av beskattning på olika band. inkomst (Bassetto och Benhabib, 2006) och många fler.

Se även

Referenser

Vidare läsning

Extern länk